Sum associativ egendom, multiplikation, exempel, övningar

De associativ egenskap av summan representerar den associerande karaktären hos operationen tillägg i olika matematiska uppsättningar. Det relaterar tre (eller fler) element i dessa uppsättningar, kallade A, B och C, så att det alltid är uppfyllt:

a + (b + c) = (a + b) + c

På detta sätt är det garanterat att oavsett hur man grupperar för att genomföra operationen är resultatet detsamma.

Figur 1. Vi använder den associativa egenskapen till summan många gånger när vi gör aritmetiska och algebraiska operationer. (Ritning: Freepik Composition: F. Zapata)

Men det bör noteras att associativ egendom inte är synonymt med kommutativ egendom. Det vill säga vi vet att ordningen på tillägg inte ändrar summan eller att ordningen på faktorerna inte förändrar produkten. Så för summan kan du skriva så här: A + B = B + A.

I den associativa egenskapen är det emellertid annorlunda, eftersom ordningen på de element som ska läggas till upprätthålls och vilka förändringar som är den verksamhet som körs först. Vilket innebär att det inte spelar någon roll (B+C) och till detta resultat lägg till, att börja lägga till B och till resultatet lägg till C.

Många viktiga operationer som summan är associerande, men inte alla. Till exempel i subtraktionen av verkliga siffror händer det att:

A - (b - c) ≠ (a - b) - c

Ja a = 2, b = 3, c = 1, sedan:

2- (3 - 1) ≠ (2 - 3) - 1

0 ≠ -2

[TOC]

Associativ multiplikationsegenskap

Som gjordes för summan indikerar multiplikationens associativa egenskap att:

A ˟ (B ˟ C) = (A ˟ B) ˟ C

Kan tjäna dig: summan av polynomer, som görs, exempel, övningar

När det gäller uppsättningen av verkliga siffror är det lätt att verifiera att det alltid är. Till exempel, med värden a = 2, b = 3, c = 1, måste du:

2 _˟ (3 _˟ 1) = (2 _˟  3) _˟ 1 → 2 _˟ 3 = 6 _˟ 1

6 = 6

De verkliga siffrorna uppfyller den associativa egenskapen för både summan och multiplikation. Å andra sidan, i en annan uppsättning, som vektorerna, är summan associerande, men tvärprodukten eller vektorprodukten är inte.

Applikationer av den associativa egenskapen för multiplikation

En fördel som de verksamheter där den associativa egendomen är uppfylld är att gruppera på det mest praktiska sättet uppfylls. Detta underlättar mycket upplösning.

Anta till exempel att det i ett litet bibliotek finns 3 hyllor med 5 underhållning vardera. I varje underhållning finns det 8 böcker. Hur många böcker som finns totalt?

Vi kan utföra operationen enligt följande: Totala böcker = (3 x 5) x 8 = 15 x 8 = 120 böcker.

Eller så: 3 x (5 x 8) = 3 x 40 = 120 böcker.

figur 2. En tillämpning av den associativa egenskapen för multiplikation är att beräkna antalet böcker på varje hylla. Bild skapad av f. Zapata.

Exempel

-I uppsättningarna av naturliga, hela, rationella, verkliga och komplexa siffror uppfylls summan och multiplikationen med multiplikation.

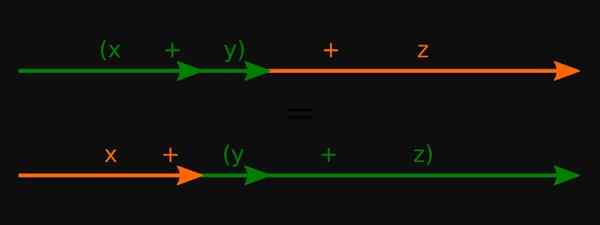Figur 3. För verkliga siffror uppfylls summan associerande egendom. Källa: Wikimedia Commons.

-För polynom tillämpar de också i dessa operationer.

-I fall av subtraktionsoperationer, uppdelning och exponentiering uppfylls inte associerande egendom i verkliga antal eller polynomier.

Kan tjäna dig: ortoedro: formler, område, volym, diagonal, exempel

-När det gäller matriser uppfylls den associativa egenskapen för summan och multiplikationen, även om kommutiviteten i det senare fallet inte uppfylls inte. Detta innebär att med tanke på matriser A, B och C är det sant att:

(A X B) X C = A X (B X C)

Men ... a x b ≠ b x a

Associativ egendom i vektorer

Vektorer bildar en annan uppsättning än verkliga siffror eller komplexa siffror. Verksamheten som definieras för uppsättningen av vektorer är något annorlunda: det finns summa, subtraktion och tre typer av produkter.

Summan av vektorer möter den associativa egenskapen, liksom siffror, polynomer och matriser. När det gäller skalprodukterna, klättring efter vektor och kors som görs mellan vektorer, möts den senare inte, men den skalära produkten, som är en annan typ av operation mellan vektorer, uppfyller den med hänsyn till följande:

-Produkten av en skalar för en vektor resulterar i en vektor.

-Och genom att klättra två vektorer är det en skalar.

Därför med tanke på vektorerna v, eller och W, Och dessutom en skalär λ, är det möjligt att skriva:

-Summan av vektorer: v +(eller + W ) = (v + eller) + W

-Skalprodukt: λ (v • eller ) = (λv) • eller

Det senare är möjligt tack vare vad v • eller Det är en skalar och λv Det är en vektor.

Dock:

v × (eller × W ) ≠ (v × eller)×W

Polynomfaktorisering genom att gruppera termer

Denna applikation är mycket intressant, eftersom som nämnts ovan hjälper associativ egendom att lösa vissa problem. Summan av monomialer är associerande och detta kan användas för att faktor när en uppenbar gemensam faktor inte visas vid första anblicken.

Kan tjäna dig: konvex polygon: definition, element, egenskaper, exempel

Anta till exempel att det uppmanas att faktor: x³ + 2x² + 3x +6. Detta polynom saknar en gemensam faktor, men låt oss se vad som händer om den är grupperad på detta sätt:

x³ + 2x² + 3x +6 = (x³ + 2x²) + (3x +6)

Den första parentesen har som en vanlig faktor x²:

x³ + 2x² = x² (x+2)

Under den andra är den vanliga faktorn 3:

3x +6 = 3 (x + 2)

Så:

x³ + 2x² + 3x +6 = x²(x+ 2)+ 3 (x+ 2)

Nu finns det en uppenbar gemensam faktor, som är x+2:

x²(x+ 2)+ 3 (x+ 2) = (x+ 2) (x²+3)

Övningar

- Övning 1

Byggnaden av en skola har 4 våningar och i var och en finns det 12 klassrum med 30 skrivbord inuti. Hur många skrivbord har skolan totalt?

Lösning

Detta problem löses genom att tillämpa den associerande egenskapen för multiplikation, låt oss se:

Totalt antal skrivbord = 4 våningar x 12 Klassrum /golv x 30 skrivbord /klassrum = (4 x 12) x 30 skrivbord = 48 x 30 = 1440 skrivbord.

O Om föredraget: 4 x (12 x 30) = 4 x 360 = 1440 skrivbord

- Övning 2

Med tanke på polynomerna:

A (x) = 5x³ + 2x² -7x + 1

B (x) = x⁴ +6x³ -5x

C (x) = -8x² +3x -7

Applicera den associerande egenskapen för summan för att hitta (x) + b (x) + c (x).

Lösning

De två första kan grupperas och resultatet lägger till det tredje:

A (x) + b (x) = [5x³ + 2x² -7x + 1] + [x⁴ +6x³ -5x] = x⁴ + 11x³+ 2x² -12x +1

Polynom C (x) läggs omedelbart till:

[x⁴ + 11x³+ 2x² -12x +1] + [-8x² +3x -7] = x⁴ + 11x³ - 6x² -9x -6

Läsaren kan verifiera att resultatet är identiskt om det löses med alternativ A (x) + [b (x) + c (x)]].

Referenser

1. Jiménez, r. 2008. Algebra. Prentice hall.
2. Matematik är kul. Kommutativa, associerande och distriktslagar. Återhämtat sig från: Mathisfun.com.
3. Matematiklager. Definition av associativ egendom. Återhämtat sig från: Mathwarehouse.com.
4. Forskning. Associerande och kommutativ egendom för tillägg och multiplikation (med exempel). Återhämtat sig från: forskning.com.
5. Wikipedia. Associativ egenskap. Hämtad från: i.Wikipedia.org.