Hemsida
Matematik
Begränsningsegenskaper (med exempel)

Matematik

Begränsningsegenskaper (med exempel)

De Begränsningsegenskaper De är uppsättningen av algebraiska regler och förfaranden som används för att bestämma dem. Gränsbegreppet är viktigt för beräkning och att hitta dess värde behöver inte vara en komplicerad uppgift, förutsatt att dess egenskaper hanteras med lätthet.

Nedan finns en lista över de viktigaste, åtföljda av applikationsexempel.

Gränserna och dess egenskaper är grunden för beräkningen. En mycket speciell gräns visas i figuren: derivatet för en f (x) -funktion

Låt B, C, N, A och B verkliga siffror och F och g Sådana funktioner som verifierar följande:

$\lim_x\rightarrow cf(x)=A$
$\lim_x\rightarrow cg(x)=B$

Då har du följande egenskaper:

1. Direkt ersättningsgräns

I första hand kan gränsen för en funktion f när x → c beräknas direkt ersätta x = c i funktionen. Om funktionen finns vid x = c är gränsen:

$\lim_x \rightarrow c f(x)=f(c)$ Men inte nödvändigtvis måste funktionen definieras vid x = c så att gränsen finns. Tanken är att närma sig så mycket du vill till värdet på x = c och se vad som händer med funktionen i det fallet.

Exempel

Hitta gränsen för f (x) = x² När x → 4

Lösning

Gränsen löser helt enkelt genom att ersätta x = 4 i f (x) = x², Eftersom det inte finns några besvär att genomföra operationen:

$\lim_x\rightarrow 4x^2=4^2=16$ 2. Det unika med gränsen

Om gränsen för en funktion f (x) när x → c finns och är värt l, sa att gränsen är unik.

Därför sidogränserna, som är de när x → c^- (Läs “X tenderar att C från vänster”) och när X → C⁺(Det står "X tenderar att c till höger"), båda finns och har samma värde l, även om funktionen inte definieras i x = c.

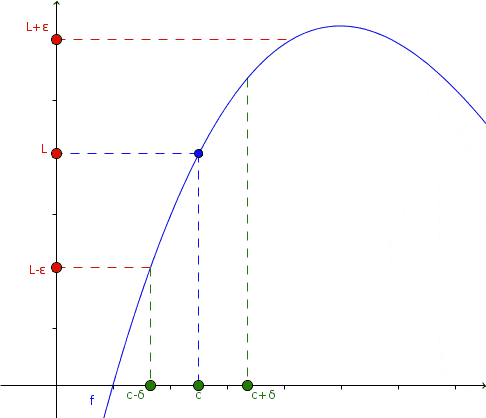I denna animation presenteras konceptet med gräns: När X tenderar till ett visst värde C, närmar sig både till vänster och höger, tenderar värdet på funktionen att l. Inte nödvändigtvis definieras funktionen i x = c. Källa: Wikimedia Commons.

I animationen observeras detta tillvägagångssätt och vad som händer med funktionen i det fallet: oavsett om den närmar sig till vänster och till höger till x = c är värdet på funktionen i sin tur nära L.

Kan tjäna dig: minsta rutor

Matematiskt uttrycker detta sätt:

$\lim_x\rightarrow c^-f(x)=\lim_x\rightarrow c^+f(x)=\lim_x\rightarrow cf(x)=L$ Sidogränserna tillåter att veta när en gräns finns eller inte, för om de inte finns eller om de skiljer sig är det säkert att gränsen för funktionen när x → c inte finns.

Exempel

Beräkna gränsen för f (x) när x → 1 om den finns, där f (x) ges av:

Lösning

Detta är en funktion av delar eller definieras i bitar, som består av rad 4 -x för värdena på x < 1 y en la parábola 4 - x² När X är lika med 1 eller större än 1.

Vi kan närma oss x = 1 från vänster, i detta fall tas den del av funktionen som är giltig för x<1:

Eftersom sidogränserna är desamma följer det att gränsen för funktionen när x → 1 finns och är värt 3.

3. Konstant

Gränsen för en konstant är värdet på nämnda konstant, oavsett värdet som variabeln tenderar:

$\lim_x\rightarrow cb=b .$

Exempel

Beräkna:

$\lim_x\rightarrow 1\pi$ Lösning

$\lim_x\rightarrow 1\pi= \pi$

4. Identitetsfunktionsbegränsning

Om f (x) = x är det alltid uppfyllt att:

$\lim_x\rightarrow cx=c$

Exempel

Beräkna:

$\lim_x\rightarrow 2x$ Lösning

$\lim_x\rightarrow 2x=2$

5. Produktgräns för en konstant genom en funktion

I det här fallet går konstanten ut ur gränsen och rör sig för att multiplicera den, så här:

$\lim_x\rightarrow c\left [b\cdot f(x) \right ]=b\cdot \lim_x\rightarrow c f(x)=b\cdot A$ Exempel

Beräkna, om det finns, följande gräns:

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]$ Lösning

Constant 5 är utanför multiplicerar till gränsen och ersättningsegenskapen tillämpas:

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]=5\cdot \lim_x\rightarrow -2 x^3=5\cdot (-2)^3=-40$

6. Summan

Gränsen för summan av två funktioner F och g Det är summan av gränserna:

$\lim_x\rightarrow c\left [ f(x)+g(x) \right ]=\lim_x\rightarrow c f(x)+\lim_x\rightarrow cg(x)=A+B$

Exempel

Hitta följande gräns om den finns:

Kan tjäna dig: Set Theory: Egenskaper, element, exempel, övningar

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ]$ Lösning

Egenskapen till summan av gränserna tillämpas först och sedan för direkt ersättning, eftersom operationerna inte ger svårigheter:

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ] = \lim_\theta \rightarrow \pi cos\: \: \theta + \lim_\theta \rightarrow \pisen\: \: \theta=cos\: \pi +sen\: \pi =-1$

7. Subtraktionsgräns

När det gäller gränsen för subtraktionen av två funktioner, fortsätt på ett analogt sätt att för summan: gränsen för subtraktionen är subtraktionen av gränserna:

$\lim_x\rightarrow c \left [f(x) - g(x) \right ]=A-B$

Exempel

Beräkna följande gräns:

$\lim_x \rightarrow 0 [sec\: x - e^x ]$ Lösning

Egenskapen för subtraktionsgränsen för två funktioner tillämpas och sedan den direkta ersättningen, eftersom alla operationer kan utföras utan problem:

$\lim_x \rightarrow 0 [sec\: x - e^x ]=\lim_x \rightarrow 0 sec\: x -\lim_x \rightarrow 0 e^x = sec\: 0-e^0=1-1=0$

8. Produktgräns

Produktgränsen för två funktioner F och g Det är produkten av gränserna:

$\lim_x \rightarrow c [f(x)\cdot g(x) ]=\lim_x \rightarrow c f(x) \cdot \lim_x \rightarrow c g(x) = A\cdot B$ Exempel

Beräkna denna gräns:

$\lim_x \rightarrow 0 cos\: x\cdot (1-x^2^)$

Lösning

$\lim_x \rightarrow 0 cos\: x\cdot (1-x^2^)=\lim_x \rightarrow 0 cos\: x\cdot \lim_x \rightarrow 0 (1-x^2^)=cos\: 0\cdot (1-0^2)=1$

9. Kvotförhållandet

Gränsen för förhållandet mellan två funktioner F och g Det är kvoten i gränserna, förutsatt att gränsen för g (x) när x → c skiljer sig från 0, eftersom uppdelningen med 0 inte är definierad. Så:

$\lim_x \rightarrow c \left [ \fracf(x)g(x) \right ]=\frac\lim_x \rightarrow c f(x)\lim_x \rightarrow c g(x)=\fracAB; \: \: \textupcon\: B\neq 0$

Exempel

Beräkna, om det finns, värdet på följande gräns:

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]$ Lösning

I första hand tillämpas egenskapsgränsen för att få kvoten för gränserna:

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]=\frac\lim_x \rightarrow -3 2x-6\lim_x \rightarrow -3 x^2+5$

Egenskapen för ersättningsegenskaper tillämpas nu för att hitta varje gräns:

$\lim_x \rightarrow -3 2x-6=2\cdot (-3)-6=-12$ $\lim_x \rightarrow -3 x^2+5= (-3)^2+5=14$

Och eftersom B ≠ 0 är den sökande gränsen kvoten A/B:

$\lim_x \rightarrow -3 \frac2x-6x^2+5=\frac-1214=\frac-67$

10. Begränsa

Gränsen för en kraft av exponent n, motsvarar den gräns som höjs till nämnda kraft, enligt följande:

$\lim_x \rightarrow c \left [f(x) \right ]^n=\left [\lim_x \rightarrow c f(x) \right ]^^n$ Fall 1: Gränsen för en X -kraft

Om du till exempel har gränsen för en X -kraft resulterar det:

$\lim_x \rightarrow c x^n=\left [\lim_x \rightarrow c x \right ]^n$

Enligt egendom 4 är denna gräns:

Kan tjäna dig: Numeriska analogier: Typer, applikationer och övningar

$\lim_x \rightarrow c x^n=c^n$

Fall 2: Rotgränsen

En n-denna rot kan skrivas i form av en fraktionerad exponent, därmed::

$\lim_x \rightarrow c \sqrt[n]f(x)=\sqrt[n]\lim_x \rightarrow c f(x)$

Viktig: Om rotindexet är jämnt är det nödvändigt att gränsen för f (x) när x → c är större än eller lika med 0, eftersom det inte finns några riktiga par negativa mängder.

Exempel

Bestäm, tillämpa de tidigare egenskaperna, följande gränser om de finns:

$a)\: \lim_x \rightarrow -2 (x+5)^^3$

$b)\: \lim_x \rightarrow 3 \sqrt2x-1$

Lösning till

Genom egenskap av gränsen för en kraft och direkt substitution erhålls det:

$\lim_x \rightarrow -2 (x+5)^^3= \left [\lim_x \rightarrow -2 (x+5) \right ]^3=(-2+5)^3=27$

Lösning B

$\lim_x \rightarrow 3 \sqrt2x-1=\sqrt\lim_x \rightarrow 3 \left (2x-1 \right )=\sqrt(2\cdot 3-1)=\sqrt5$

elva. Begränsa

För att hitta gränsen för en baseksponentiell B och exponent F (x) måste basen för funktionen F (x) höjas enligt följande:

$\lim_x \rightarrow c \left [b^f(x) \right ]=b^\lim_x \rightarrow cf(x)$

Exempel

Hitta om det finns följande gräns:

$\lim_x \rightarrow 1 \left [e^x^^2 \right ]$ Lösning

I denna gräns är basen numret E och funktionen f (x) = x², Därför måste du först beräkna X -gränsen² När X tenderar till 1:

$\lim_x \rightarrow 1 x^2=1^^2=1$

Därefter tillämpas egenskapen till exponentiell gräns:

$\lim_x \rightarrow 1 e^^x^2=e^^1=e$

12. Exponentiell potentialfunktionsbegränsning

Gränsen när x → c för en funktion f (x), som i sin tur är upphöjd till en annan funktion g (x) uttrycks av:

$\lim_x \rightarrow c \left [f(x)^g(x) \right ]=\left [\lim_x \rightarrow c f(x) \right ]^\lim_x \rightarrow c g(x)$

Exempel

Beräkna följande gräns om den finns:

$\lim_x \rightarrow -1 (x-1)^^2x$

Lösning

För att tillämpa föregående egenskap identifieras de först f (x) = x-1 och g (x) = 2x och sedan beräknas respektive gränser:

$\lim_x \rightarrow -1 (x-1)=-1-1=-2$

$\lim_x \rightarrow -1 2x=2\cdot (-1)=-2$ Till sist:

$\lim_x \rightarrow -1 (x-1)^2x=\left [\lim_x \rightarrow -1 (x-1) \right ]^\lim_x \rightarrow -1 2x=(-2)^-2=\left (\frac1-2 \right )^2=\frac14$ Referenser

Ayres, f. 2000. Beräkning. 5ed. MC Graw Hill.
Leithold, L. 1992. Beräkning med analytisk geometri. Harla, s.TILL.
Gratis matematiktexter. Gränser. Återhämtat sig från: matematik.Liibretexts.org.
Matemovil. Lagar och begränsar egenskaper. Återhämtad från: Matemovil.com.
Larson, r. 2010. Beräkning av en variabel. 9na. Utgåva. McGraw Hill.
Purcell, E. J., Varberg, D., & Rigdon, s. OCH. (2007). Beräkning. Mexiko: Pearson Education.
Universumsformler. Begränsningsegenskaper. Återhämtat sig från: universalformulor.com

Begränsningsegenskaper (med exempel)

1. Direkt ersättningsgräns

Exempel

Lösning

2. Det unika med gränsen

Exempel

Lösning

3. Konstant

Exempel

Lösning

4. Identitetsfunktionsbegränsning

Exempel

Lösning

5. Produktgräns för en konstant genom en funktion

Exempel

Lösning

6. Summan

Exempel

Lösning

7. Subtraktionsgräns

Exempel

Lösning

8. Produktgräns

Exempel

Lösning

9. Kvotförhållandet

Exempel

Lösning

10. Begränsa

Fall 1: Gränsen för en X -kraft

Fall 2: Rotgränsen

Exempel

Lösning till

Lösning B

elva. Begränsa

Exempel

Lösning

12. Exponentiell potentialfunktionsbegränsning

Exempel

Lösning

Referenser

Bästa artiklarna

Termometerdelar och huvudfunktioner

Termometern är ett instrument som används för att mäta temperaturer. Beroende på typ av termometer k...

Manuel Machado Biografi, litterär stil, ideologi och verk

Manuel Machado Ruiz (1874-1947) var en spansk poet och dramatiker som utvecklade sitt arbete inom mo...

$\lim_x\rightarrow 4x^2=4^2=16$ 2. Det unika med gränsen

$\lim_x\rightarrow 1\pi$ Lösning

$\lim_x\rightarrow 2x$ Lösning

$\lim_x\rightarrow c\left [b\cdot f(x) \right ]=b\cdot \lim_x\rightarrow c f(x)=b\cdot A$ Exempel

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]$ Lösning

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ]$ Lösning

$\lim_x \rightarrow 0 [sec\: x - e^x ]$ Lösning

$\lim_x \rightarrow c [f(x)\cdot g(x) ]=\lim_x \rightarrow c f(x) \cdot \lim_x \rightarrow c g(x) = A\cdot B$ Exempel

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]$ Lösning

$\lim_x \rightarrow c \left [f(x) \right ]^n=\left [\lim_x \rightarrow c f(x) \right ]^^n$ Fall 1: Gränsen för en X -kraft

$\lim_x \rightarrow 1 \left [e^x^^2 \right ]$ Lösning

$\lim_x \rightarrow -1 (x-1)^2x=\left [\lim_x \rightarrow -1 (x-1) \right ]^\lim_x \rightarrow -1 2x=(-2)^-2=\left (\frac1-2 \right )^2=\frac14$ Referenser