Förklaring av sammansatt proportionalitet, tre sammansatta regel, övningar

De Komposit eller flera proportionalitet Det är förhållandet mellan mer än två storlekar, där direkt och omvänd proportionalitet kan observeras mellan uppgifterna och det okända. Det är en mer avancerad version av enkel proportionalitet, även om de tekniker som används i båda procedurerna är lika.

Till exempel, om 7 personer behövs för att ladda ner 10 ton varor på 3 timmar, kan den sammansatta proportionaliteten användas för att beräkna hur många som behövs för att ladda ner 15 ton på 4 timmar.

Källa: Pixabay.com

För att besvara denna fråga är det bekvämt att skapa en tabell över värden för att studera och relatera storleken och okända.

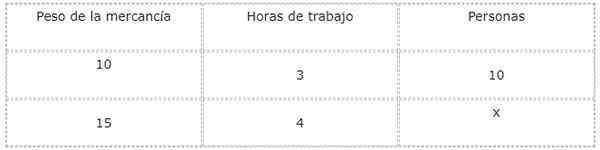
De typer av förhållanden mellan varje storlek och det nuvarande okända analyseras, vilket i detta fall motsvarar antalet människor som kommer att arbeta.

När vikten av varorna ökar ökar också antalet människor som behövs för att ladda ner. På grund av detta är förhållandet mellan vikt och arbetare direkt.

Å andra sidan, genom att öka antalet arbetare, minskar arbetstiden. På grund av detta är förhållandet mellan människor och arbetstid omvänd.

[TOC]

Hur man beräknar sammansatta proportionaliteter

För att lösa exempel som den föregående används den tre sammansatta regelmetoden mest. Detta består i att upprätta de typer av förhållanden mellan storlekar och okända och sedan representera en produkt mellan fraktioner.

När det gäller det initiala exemplet är de fraktioner som motsvarar värdentabellen enligt följande:

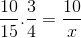
Men innan du löser och rensar det okända måste de fraktioner som motsvarar det omvända förhållandet vändas. Att för detta fall motsvarar tidsvariabeln. På detta sätt kommer operationen som ska lösas att vara:

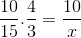
Vars enda skillnad är investeringen av fraktionen som motsvarar den variabla tiden 4/3. Värdet på X drivs och tydligt.

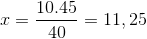
Således behövs mer än elva personer för att ladda ner 15 ton varor på 4 timmar eller mindre.

Förklaring

Proportionalitet är det ständiga förhållandet mellan storlekar som är föremål för förändringar, vilket kommer att vara symmetriskt för var och en av de inblandade storleken. Det finns direkt och omvänt proportionella förhållanden, vilket definierar parametrarna för enkel eller sammansatt proportionalitet.

Direkt tre regel

Det består av ett förhållande mellan variabler, som presenterar samma beteende när det modifieras. Det är mycket ofta vid beräkningen av procentsatser relaterade till olika storlekar på hundra, där dess grundläggande struktur uppskattas.

Som exempel kan du beräkna 15% av 63. Vid första anblicken, sa att procentandel inte kan ses på ett enkelt sätt. Men implementera regeln om tre kan du göra följande förhållande: Om 100% är 63, så är 15%, hur mycket kommer det att vara?

Kan tjäna dig: Faktorteorem: Förklaring, exempel, övningar

100%-63

15%-x

Och motsvarande operation är:

(femton% . 63) / 100% = 9,45

Där procentuella tecknen förenklas och siffran 9.45 som representerar 15% av 63 uppnås.

Tre omvända regel

Som namnet antyder är i detta fall förhållandet mellan variablerna motsatt. Det omvända förhållandet måste upprättas innan du fortsätter till beräkningen. Hans förfarande är homolog med den tre direkta regeln, med undantag för investeringar i den fraktion som ska beräknas.

Till exempel behöver 3 målare 5 timmar för att avsluta en vägg. Hur många timmar slutade 4 målare?

I detta fall är förhållandet omvänt, eftersom genom att öka antalet målare bör arbetstiden minska. Förhållandet är etablerat;

3 målare - 5 timmar

4 målare- x timmar

När förhållandet är omvänt omvänds driftsordningen. Detta är på rätt sätt;

(3 målare) . (5 timmar) / 4 målare = 3,75 timmar

Termen målare förenklas och resultatet är 3,75 timmar.

Skick

För att vara i närvaro av en förening eller multipel proportionalitet är det nödvändigt att hitta båda typerna av förhållanden mellan storlekar och variabler.

- Direkt: Variabeln presenterar samma beteende som det okända. Det vill säga genom att öka eller minska det ena, den andra förändras lika.

- Inverse: Variabeln presenterar ett antonymbeteende för det okända. Fraktionen som definierar denna variabel i värdentabellen måste vändas för att representera det omvänt proportionella förhållandet mellan variabel och okänd.

Verifiering av resultaten

Det är mycket vanligt att förvirra storleksordningen när man arbetar med sammansatta proportionaliteter, till skillnad från vad som händer i de vanliga proportionberäkningarna, vars natur mestadels är direkt och löslig med hjälp av en enkel tre regel.

Därför är det viktigt att undersöka den logiska ordningen på resultaten, vilket verifierar sammanhangen av siffrorna som kastas av den tre sammansatta regeln.

I det första exemplet skulle det att göra detta misstag innebära att få 20 som ett resultat. Det vill säga 20 personer att ladda ner 15 ton varor på 4 timmar.

Vid första anblicken verkar det inte som ett galet resultat, men en ökning med nästan 200% i personalen (från 7 till 20 personer) är nyfiken när ökningen av varor är 50%, och till och med med en större marginal för att utföra arbete.

Det kan tjäna dig: allmän parabola -ekvation (exempel och övningar)

På detta sätt representerar den logiska verifieringen av resultaten ett viktigt steg genom att implementera den tre sammansatta regeln.

Undanröjning

Även om en mer grundläggande karaktär när det gäller matematisk bildning, representerar clearance ett viktigt steg i fall av proportionalitet. En felaktig godkännande är tillräckligt för att ogiltigförklaras alla resultat som erhållits i ordning av tre enkla eller sammansatta.

Historia

Regeln om tre blev känd i väst genom araberna, med publikationer av flera författare. Bland dem al-jwarizmi och al-biruni.

Al-Biruni, tack vare sin multikulturella kunskap, hade tillgång till enorm information om denna praxis i sina resor till Indien och var ansvarig för den mest omfattande dokumentationen om tre regel om tre.

Det höjer i hans utredning, att Indien var det första stället där användningen av den tre regeln gjordes vanligt. Författaren försäkrar att det gjordes flytande i hans direkta, omvända och till och med sammansatta versioner.

Det exakta datumet då de tre regeln blev en del av den matematiska kunskapen i Indien är fortfarande okänd. Men det äldsta dokumentet som syftade till denna praxis, Bakhshalis manuskript, upptäcktes 1881 1881. Det är för närvarande i Oxford.

Många matematikhistoriker säkerställer att detta manuskript är från början av den nuvarande eran.

Löst övningar

Övning 1

Ett flygbolag måste flytta 1535 personer. Det är känt att med 3 plan skulle det ta 12 dagar att ta till den sista passageraren till destinationen. 450 fler människor har nått flygbolaget och två plan beordras att samarbeta med denna uppgift. Hur många dagar tar flygbolaget till den sista passageraren till sin destination?

Förhållandet mellan antalet människor och arbetsdagar är direkt, eftersom ju fler människor, fler dagar kommer att krävas för att utföra detta arbete.

Å andra sidan är förhållandet mellan flygplan och dagar omvänt proportionellt. Genom att öka mängden flygplan minskar de nödvändiga dagarna för att överföra till alla passagerare.

Värdentabellen som hänvisar till detta fall utförs.

Såsom beskrivs i det initiala exemplet måste teller och nämnaren investeras i fraktionen som motsvarar den omvända variabeln med avseende på det okända. Lämnar operationen enligt följande:

Kan tjäna dig: Beräkning av tillvägagångssätt med skillnader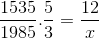

X = 71460/7675 = 9,31 dagar

För att flytta till 1985 personer som använder 5 flygplan är mer än 9 dagar nödvändiga.

Övning 2

En 25 -ton majsskörd tas till lastbilar. Det är känt att föregående år tog 8 timmar med en lön på 150 arbetare. Om lönen för detta år ökar med 35%, hur lång tid tar det att fylla lastbilarna med en 40 -ton skörd?

Innan du representerar värdentabellen måste antalet arbetare för detta år definieras. Detta ökade 35% av den ursprungliga siffran på 150 arbetare. För detta används en direkt tre regel.

100% - 150

35% - x

X = (35 . 100)/100 = 52,5. Detta är antalet ytterligare arbetare med avseende på föregående år och erhåller ett totalt antal 203 arbetare, olyckliga att runda det erhållna beloppet.

Motsvarande datatabell definieras

För detta fall representerar vikten en direkt relationvariabel med den okända tiden. Å andra sidan hanterar arbetarnas variabel en omvänd relation med tiden. Ett större antal arbetare, dagen kommer att vara kortare.

Med hänsyn till dessa överväganden och investerar den fraktion som motsvarar arbetarna, beräknas den.

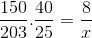
X = 40600 /6000 = 6,76 timmar

Dagen tar lite mindre än 7 timmar.

Föreslagna övningar

- Definiera 73% av 2875.

- Beräkna hur många timmar som Teresa sover, om det är känt att endast 7% av dagens sömn. Definiera hur många timmars sömn i veckan.

- En offentlig tidning 2000 var 5: e timme och använder bara två tryckmaskiner. Hur många exemplar kommer att producera på 1 timme om du använder 7 maskiner? Hur länge kommer att producera 10.000 kopior med fyra maskiner?

Referenser

1. Encyclopedia Alvarez-iniciacion. TILL. Álvarez, Antonio Álvarez Pérez. Edaf, 2001.
2. Komplett elementär och överlägsen primärinstruktionshandbok: För användning av sökande till lärare och särskilt eleverna i normala provinsskolor, volym 1. Joaquín Avendaño. Utskrift d. Dionisio Hidalgo, 1844.
3. Betyg om tillnärmning av verkliga funktioner. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3 mars. 2011.
4. Elemental aritmetik för undervisning i skolor och skolor i Centralamerika. Darío gonzález. Dricks. Arenales, 1926.
5. Studien av matematik: om matematikens studie och svårigheter. Augustus de Morgan. Baldwin och Cradock, 1830.