Vad är spänningsdelaren? (Med exempel)

han Spänningsdelare o Spänningsdelaren består av en förening av motstånd eller impedanser i serie anslutna till en källa. På detta sätt spänningen V Levereras av källans - ingångsspänning - distribueras proportionellt i varje element, enligt OHM: s lag:

V_Yo = Jag.Z_Yo.

Där v_Yo Det är spänningen i kretselementet, jag är den ström som cirkulerar genom det och z_Yo motsvarande impedans.

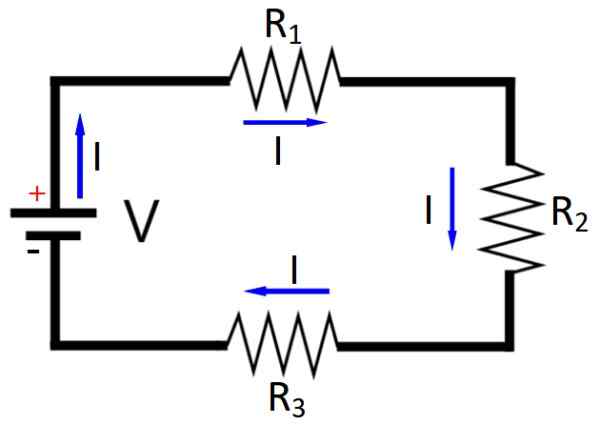
Figur 1. Den resistiva spänningsdelaren består av seriemotstånd. Källa: Wikimedia Commons.

När du ordnar källan och elementen i en sluten krets måste Kirchhoffs andra lag.

Till exempel, om den krets som ska beaktas är rent resistiv och en 12 -volt källa är tillgänglig, helt enkelt med att ha två identiska seriemotstånd med den källan, kommer spänningen att delas: i varje motstånd kommer det att finnas 6 volt. Och med tre identiska motstånd erhålls 4 V i varje.

När källan representerar en spänningsklättring, sedan v = +12 v. Och i varje motstånd finns det spänningsdroppar som är representerade med negativa tecken: - 6 V respektive - 6 V. Det varnas lätt att Kirchoffs andra lag är uppfylld:

+12 V - 6 V - 6 V = 0 V

Härifrån kommer spänningsavdelningsnamnet, för genom seriemotstånd kan mindre spänningar enkelt erhållas från en källa med en större spänning.

[TOC]

Spänningsdelarekvationen

Låt oss fortsätta överväga en rent resistiv krets. Vi vet att den nuvarande I som korsar en krets med seriemotstånd anslutna till en källa som visas i figur 1, är densamma. Och enligt Ohms lag och Kirchoffs andra lag:

Kan tjäna dig: vad är nettokraften? (Med exempel)

V = gå₁ + GÅ₂ + GÅ₃ +... gå_Yo

Där r₁, R₂... r_Yo Representerar varje seriemotstånd i kretsen. Därför:

V = i ∑ r_Yo

Då visar sig strömmen vara:

I = v / ∑ r_Yo

Låt oss nu beräkna spänningen i ett av motståndet, motståndet r_Yo Till exempel:

V_Yo = (V / ∑ r_Yo) R_Yo

Den föregående ekvationen skrivs om enligt följande och vi har redan spänningsavdelningsregeln för ett batteri- och N -seriemotstånd:

Spänningsdelare med 2 motstånd

Om vi ​​har en spänningskrets med två motstånd, förvandlas den tidigare ekvationen till:

Och i det speciella fallet där r₁ = R₂, V_Yo = V/2, oavsett strömmen, som anges i början. Detta är den enklaste spänningsdelaren av alla.

I följande figur är schemat för denna divisor, där V, ingångsspänningen symboliseras som V_i, och v_Yo Det är den spänning som erhålls genom att dela spänningen mellan motståndet r₁ och r₂.

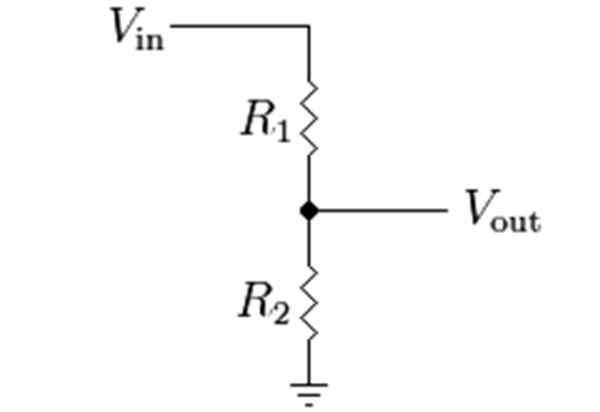figur 2. Spänningsdelare med 2 serie motstånd. Källa: Wikimedia Commons. Se sida för författare/cc by-sa (http: // creativecommons.Org/licenser/BY-SA/3.0/).

Löst exempel

Spänningsavdelningsregeln appliceras i två resistiva kretsar för att erhålla mindre spänningar.

- Exempel 1

En källa på 12 V är tillgänglig, som måste delas upp i 7 V och 5 V genom två R -motstånd₁ och r₂. Ett fast motstånd på 100 Ω och ett variabelt motstånd vars intervall är mellan 0 och 1kΩ är tillgängligt. Vilka alternativ finns det för att konfigurera kretsen och ställa in motståndsvärdet r₂?

Lösning

För att lösa denna övning kommer spänningsdelaren för två motstånd att användas:

Antar r₁ Det är motståndet som är vid en spänning på 7 V och det placeras det fasta motståndet r₁ = 100 Ω

Okänd motstånd r₂ Det måste vara 5 V:

Kan tjäna dig: kosmiskt damm

Och r₁ A 7 V:

5 (r₂ +100) = 12 r₂

500 = 7 r₂

R₂ = 71.43 Ω

Du kan också använda den andra ekvationen för att få samma värde, eller ersätta det resultat som erhållits för att kontrollera jämlikhet.

Om det fasta motståndet nu placeras som R₂, Då kommer det att vara r₁ är 7 V:

5 (100 + r₁) = 100 x 12

500 + 5R₁ = 1200

R₁ = 140 Ω

På samma sätt är det möjligt att verifiera att detta värde uppfyller den andra ekvationen. Båda värdena finns i intervallet av variabel motstånd, därför är det möjligt att implementera den begärda kretsen på båda sätten.

- Exempel 2

En DC direktvoltmeter för att mäta spänningar i ett visst intervall är baserad på spänningsdelaren. För att bygga denna voltmeter krävs en galvanometer, till exempel den för D'Arsonval.

Detta är en mätare som upptäcker elektriska strömmar, med en graderad skala och en indikatornål. Det finns många modeller av galvanometrar, figuren är mycket enkel, med två anslutningsterminaler som är på baksidan.

Figur 3. En Galvanometer från D'Arsonval -typ. Källa: f. Zapata.

Galvanometern har ett internt motstånd R_G, som bara tolererar en liten ström, kallad maximal ström i_G. Följaktligen är spänningen genom galvanometern v_m = Jag_GR_G.

För att mäta någon spänning placeras voltmetern parallellt med det element som önskas mäta och dess inre motstånd måste vara tillräckligt stort för att inte konsumera kretsström, för annars förändrar den den.

Om vi ​​ville använda galvanometern som en mätare bör mätspänningen inte överstiga det maximala tillåtna, vilket är den maximala nålavböjningen som enheten har. Men vi antar att v_m är liten, eftersom jag_G  och r_G dom är.

Kan tjäna dig: distanskrafter

Men när serien galvanometer är ansluten till ett annat motstånd R_S, ring upp Begränsande motstånd, Vi kan utöka mätområdet i galvanometern från den lilla v_m Fram till en viss huvudspänning. När denna spänning uppnås upplever instrumentnålen den maximala avböjningen.

Designschemat är som följer:

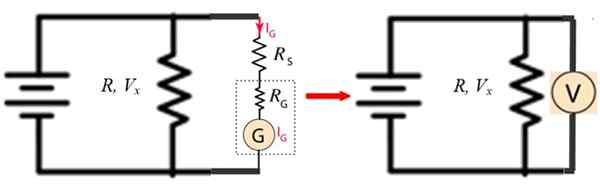Figur 4. Design av en voltmeter genom att använda en galvanometer. Källa: f. Zapata.

I figur 4 till vänster är G galvanometern och R är alla motstånd som du vill mäta spänningen V_x.

I figuren till höger visas det som kretsen med G, R_G och r_S Det motsvarar en voltmeter, som placeras parallellt med motståndet r.

Maximal skala voltmeter 1 v

Anta till exempel att det inre motståndet hos galvanometern är r_G = 50 Ω och den maximala strömmen den stöder är jag_G = 1 mA, RS -begränsningsmotståndet så att den voltmeter som är byggd med denna galvanometer mäter en maximal 1 V -spänning beräknas enligt följande:

Yo_G (R_S + R_G) = 1 v

R_S = (1 V / 1 x 10^-3 A) - r_G

R_S = 1000 Ω - 50 Ω = 950 Ω

Referenser 

1. Alexander, c. 2006. Elektriska kretsfundament. 3: e. Utgåva. MC Graw Hill.
2. Boylestad, r. 2011. Introduktion till kretsanalys. 2: a. Utgåva. Pearson.
3. Dorf, r. 2006. Introduktion till elektriska cirkuds. 7th. Utgåva. John Wiley & Sons.
4. Edminister, J. nitton nittiosex. Elektriska kretsar. Schaumserie. 3: e. Utgåva. MC Graw Hill
5. Figueroa, D. Fysisk serie för vetenskap och teknik. Vul. 5 Elektrostatisk. Redigerad av D. Figueroa. USB.
6. Hyperfysik. Voltmeter design. Återhämtat sig från: hyperfysik.Phy-astrage.Gsu.Edu.
7. Wikipedia. Spänningsdelare. Återhämtat sig från: det är.Wikipedia.org.