Serie av kraftexempel och övningar

En Kraftserie Den består av en summa av termer i form av variabelns krafter x, eller mer generellt, av X-c, var c Det är ett konstant verkligt nummer. I sammanfattningen av summan uttrycks en serie krafter på följande sätt:

∑a_n (X -c)ⁿ = a_antingen + till₁ (x - c) + a₂ (X - c)² + till₃ (X - c)³ +... + a_n (X - c)ⁿ

Där koefficienterna till_antingen, till₁, till₂... de är riktiga siffror och serien börjar vid n = 0.

Figur 1. Definition av en kraftserie. Källa: f. Zapata.

Denna serie är fokuserad på värde c det är konstant, men du kan välja det c Vara lika med 0, i vilket fall befogenheterna förenklas:

∑a_n xⁿ = a_antingen + till₁ x + a₂ x² + till₃ x³ +... + a_n xⁿ

Serien börjar med till_antingen(X-C)⁰ och till_antingenx⁰ respektive. Men vi vet det:

(X-C)⁰= x⁰ = 1

Därför till_antingen(X-C)⁰ = till_antingenx⁰ = till_antingen (Oberoende term)

Det bra med krafterna är att med dem kan du uttrycka funktioner och detta har många fördelar, särskilt om du vill arbeta med en komplicerad funktion.

När detta är fallet, istället för att direkt använda funktionen, används dess kraftutveckling, vilket kan vara lättare att härleda, integrera eller arbeta numeriskt.

Naturligtvis är allt konditionerat till seriens konvergens. En serie konvergerar när genom att lägga till en viss mängd termer erhålls ett fast värde. Och om vi lägger till fler villkor fortsätter vi att få det värdet.

[TOC]

Fungerar som kraftkraft

Som ett exempel på en funktion uttryckt som en serie kraft, låt oss ta f (x) = e^x.

Denna funktion kan uttryckas i termer av en serie krafter enligt följande:

och^x  ≈ 1 + x + (x² / 2!) + (X³ / 3!) + (x⁴ / 4!) + (x⁵ / 5!) +..

Var! = n. (N-1). (N-2). (N-3) ... och det tas 0! = 1.

Vi kommer att kontrollera med hjälp av en kalkylator, som serien effektivt sammanfaller med den uttryckligen givna funktionen. Låt oss till exempel börja göra x = 0.

Kan tjäna dig: Teoretisk sannolikhet: Hur man får ut det, exempel, övningar

Vi vet att E⁰ = 1. Låt oss se vad serien gör:

och⁰ ≈ 1 + 0 + (0² / 2!) + (0³ / 3!) + (0⁴ / 4!) + (0⁵ / 5!) +… = 1

Och nu låt oss försöka med x = 1. En kalkylator kastar det och¹ = 2.71828, Och låt oss jämföra med serien:

och¹ ≈ 1 + 1 + (1² / 2!) + (1³ / 3!) + (1⁴ / 4!) + (1⁵ / 5!) +… = 2 + 0.5000 + 0.1667 + 0.0417 + 0.0083 +... ≈ 2.7167

Med bara 5 termer har vi redan exakt sammanfall i E ≈ 2.71. Vår serie saknas bara lite mer, men när fler termer läggs till, med all säkerhet konvergerar serien till det exakta värdet på och. Representationen är exakt när N → ∞.

Om den tidigare analysen upprepas för n = 2 Mycket liknande resultat erhålls.

På detta sätt är vi säkra på att den exponentiella funktionen f (x) = e^x Det kan representeras av denna serie av krafter:

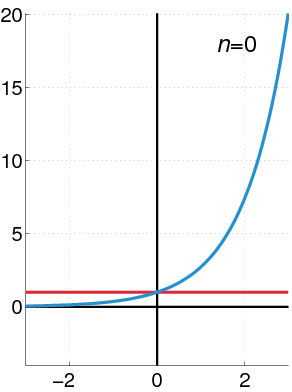figur 2. I denna animering ses det när krafterna är närmare den exponentiella funktionen eftersom fler termer tas. Källa: Wikimedia Commons.

Geometriska krafter

Funktionen f (x) = e^x Det är inte den enda funktionen som medger en seriell representation av krafter. Till exempel funktionen  F(x) = 1/1 - x  Det ser mycket ut som det kända Konvergent geometrisk serie:

∑a.rⁿ = A / 1 - r

Gör bara a = 1 och r = x för att få en lämplig serie till denna funktion, som är centrerad på c = 0:

Det är emellertid känt att denna serie är konvergent för │r│<1, por lo tanto la representación es válida únicamente en el intervalo (-1,1), aunque la función sea válida para todo x, excepto x=1.

När du vill definiera den här funktionen i ett annat intervall fokuserar den helt enkelt på ett tillräckligt värde och redo.

Hur man hittar seriens utveckling av krafter i en funktion

Varje funktion kan utvecklas i en serie krafter som är inriktade på C, så länge du har härstammat från alla beställningar vid x = c. Förfarandet använder sig av följande teorem, kallad Taylor Theorem:

Låt f (x) vara en funktion med ordningsderivat n, betecknar som F^(N), som medger en serieutveckling av krafter i intervallet Yo. Dess utveckling i Taylor Series är:

Det kan tjäna dig: vad är platsen för hela och decimalantal?

Så att:

f (x) = f (c) + f '(c) (x-c) + f "(c) (x-c)² /2 + f "(c) (x-c)³ /6 +... r_n

Där r_n, Vilket är seriens nion återstod:

När c = 0 ser serien Maclaurin -serie.

Denna serie som ges här är identisk med serien som ges i början, först nu finns det ett sätt att uttryckligen hitta koefficienterna för varje term, som ges av:

Det måste dock säkerställas att serien förmedlar funktionen som du vill representera. Det händer att inte varje Taylor -serie nödvändigtvis konvergerar till F (x) som var i åtanke vid beräkningen av koefficienterna till_n.

Detta händer eftersom de kanske härrör från funktionen, utvärderad i x = c sammanfaller med samma värde på de härrörande från en annan, även i x = c. I detta fall skulle koefficienterna vara desamma, men utvecklingen skulle vara tvetydig genom att inte ha säkerheten som funktionen motsvarar.

Lyckligtvis finns det ett sätt att veta:

Konvergenskriterier

För att undvika tvetydighet, om r_n → 0 När n → ∞ för alla x i intervall I konvergerar serien till f (x).

Träning

- Motion Löst 1

Hitta de geometriska krafterna för funktion f (x) = 1/2 - x fokuserad på c = 0.

Lösning

Den givna funktionen måste uttryckas på ett sätt som matchar så mycket som möjligt med 1 / 1- x, vars serie är känd. Därför skriver vi om teller och nämnaren utan att förändra det ursprungliga uttrycket:

1/2 - x = (1/2) / [1 - (x / 2)]

Eftersom ½ är konstant går den ut ur summan, och detta är skrivet i termer av den nya variabeln x/2:

Kan tjäna dig: konjugerad binomial: hur det är löst, exempel, övningar

Observera att x = 2 inte tillhör funktionens domän och enligt konvergenskriterierna i avsnittet Kraftgeometrisk serie, Utveckling är giltig för │x/2│< 1 o equivalentemente -2 < x < 2.

- Motion Löst 2

Hitta de första 5 termerna i MacLaurins serieutveckling av funktionen f (x) = sen x.

Lösning

Steg 1

Först är derivaten:

-Härrörande från ordning 0: det är samma funktion f (x) = sen x

-Första derivat: (sin x) '= cos x

-Andra derivat: (sin x) "= (cos x) '= - sin x

-Tredje derivat: (sin x) "= (-sen x) '= - cos x

-Fjärde derivat: (sin x) "= (- cos x) '= sin x

Steg 2

Sedan utvärderas varje derivat vid x = c, liksom en utveckling av maclaurin, c = 0:

synd 0 = 0; cos 0 = 1; - sen 0 = 0; -Cos 0 = -1; synd 0 = 0

Steg 3

Koefficienterna är byggda till_n;

till_antingen = 0/0! = 0; till₁ = 1/1! = 1; till₂ = 0/2! = 0; till₃ = -1 / 3!; till₄ = 0/4! = 0

Steg 4

Slutligen är serien sammansatt enligt:

synd x ≈ 0.x⁰ + 1. x¹ + 0 .x² - (1/3!) x³ + 0.x⁴... = x - (1/3!)) x³  +..

Behöver läsaren fler termer? Hur många fler är serien närmare funktionen.

Observera att det finns ett mönster i koefficienterna, följande icke -nollterm är att₅ Och allt udda index skiljer sig också från 0, växlar skyltarna, så att:

Sen x ≈ x - (1/3!)) x³  + (1/5!)) x⁵ - (1/7!)) x⁷  +.. .

Det är kvar som träning att verifiera, du kan använda kvotförhållandet För seriekonvergens.

Referenser

1. CK-12 Foundation. Power Series: Representation av funktioner och operationer. Återhämtat sig från: CK12.org.
2. Engler, a. 2019. Integrerad kalkyl. National University of the Coast.
3. Larson, r. 2010. Beräkning av en variabel. 9na. Utgåva. McGraw Hill.
4. Gratis matematiktexter. Kraftserie. Återhämtat sig från: matematik.Liibretexts.org.
5. Wikipedia. Kraftserie. Återhämtad från: är.Wikipedia.org.