Vad är balansen i partikeln? (Med exempel)

han partikelbalans Det är ett tillstånd där en partikel är när de yttre krafterna som verkar på dem upphävs med varandra. Detta innebär att det upprätthåller ett konstant tillstånd, så att det kan uppstå på två olika sätt beroende på den specifika situationen.

Den första är att vara i statisk jämvikt, där partikeln är rörlig; Och den andra är den dynamiska balansen, där summan av krafter avbryts, men ändå har partikeln enhetlig rätlinjig rörelse.

Figur 1. Balance Rock Formation. Källa: Pixabay.

Partikelmodellen är ett mycket användbart tillvägagångssätt för att studera en kropps rörelse. Den består av att anta att hela kroppens massa är koncentrerad i en enda punkt, oavsett objektets storlek. På detta sätt kan du representera en planet, en bil, en elektron eller en biljardkula.

[TOC]

Den resulterande kraften

På den punkt som representerar objektet är där krafterna som påverkar det lagen. Alla dessa krafter kan ersättas av en singel som gör samma effekt, som kallas resulterande kraft antingen Nettokraft Och det betecknas som f_R eller f_N.

Enligt Newtons andra lag, när det finns en obalanserad resulterande kraft, upplever kroppen en acceleration som är proportionell mot att tvinga:

F_R = m.till

Var till Det är accelerationen som objektet förvärvar tack vare kraftens verkan och m Det är objektets massa. Vad händer om kroppen inte accelereras? Precis vad som indikerades i början: Kroppen är i vila eller rör sig med enhetlig rätlinjig rörelse, som saknar acceleration.

För en partikel i balans är det giltigt att säkerställa att:

F_R = 0

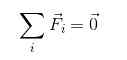
Eftersom tillsats av vektorer inte nödvändigtvis innebär modulerna, måste vektorer sönderdelas. Således är det giltigt att uttrycka:

F_x = m.till_x = 0; F_och = m.till_och = 0; F_z = m.till_z = 0

Gratis kroppsdiagram

För att visualisera de krafter som verkar på partikeln bör ett fritt kroppsdiagram göras, där alla krafter som verkar på objektet representeras av pilar.

Kan tjäna dig: Jordens magnetosfär: Egenskaper, struktur, gaser

De tidigare ekvationerna är vektor natur. Genom att sönderdela krafterna kännetecknas de av tecken. På detta sätt möjliggörs det att summan av dess komponenter är noll.

Följande är viktiga indikationer för att ritningen ska vara användbara:

- Välj ett referenssystem där det största antalet krafter finns på koordinataxlarna.

- Vikten dras alltid vertikalt ner.

- När det gäller existor två eller flera ytor i kontakt finns det normala krafter, som alltid ritas genom att trycka kroppen och vinkelrätt mot ytan som utövar den.

- För en partikel i jämvikt kan det finnas friktion parallellt med kontaktytan och motsätta sig den möjliga rörelsen, om partikeln betraktas i vila, eller definitivt i opposition, om partikeln rör sig med MRU (enhetlig rektilinär rörelse).

- Om det finns ett rep dras spänningen alltid längs den och drar kroppen.

Sätt att tillämpa balansvillkoret

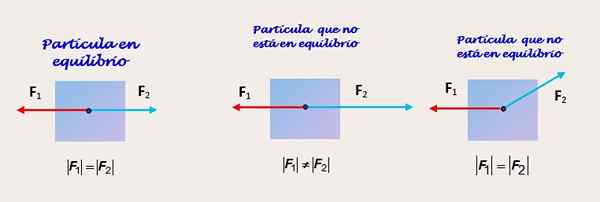figur 2. Två tillämpade krafter på olika sätt på samma kropp. Källa: Självgjord.

Två krafter med lika stor storlek och riktning och motsatta sinnen

Figur 2 visar en partikel på vilken två krafter verkar. I figuren till vänster får partikeln verkan av två krafter f₁ och f₂ som har samma storlek och agerar i samma riktning och i motsatta sinnen.

Partikeln är i balans, men ändå med informationen förutsatt är det inte möjligt att veta om balansen är statisk eller dynamisk. Mer information om tröghetsreferenssystemet behövs från vilket objektet observeras.

Två krafter av olika storlek, lika riktning och motsatta sinnen

Centerfiguren visar samma partikel, som den här gången inte är i jämvikt, eftersom storleken på kraften f₂ är större än F₁. Därför finns det en obalanserad kraft och objektet har en acceleration i samma riktning som f₂.

Kan tjäna dig: Darcy Law

Två krafter med lika stor storlek och olika riktningar

Slutligen i figuren till höger observerar vi en kropp som inte heller är i balans. Även om f₁ och f₂ De har samma storlek, kraften f₂ Det är inte i samma riktning som 1. Den vertikala komponenten i f₂ Det motverkas inte av någon annan och partikeln upplever en acceleration i den riktningen.

Tre krafter med olika riktningar

Kan en partikel överlämnas till tre krafter vara i balans? Ja, så länge när du placerar ett spets av var och en är den resulterande figuren en triangel. I detta fall är vektor summan noll.

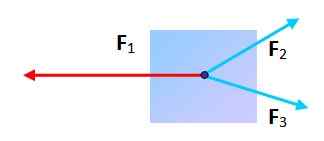Figur 3. En partikel som är föremål för verkan av 3 krafter kan vara i balans. Källa: Självgjord.

Friktion

En kraft som ofta ingriper i partikelns balans är statisk friktion. Det beror på interaktionen mellan objektet som representeras av partikeln med ytan på en annan. Till exempel modelleras en bok i statisk jämvikt på ett lutande bord som en partikel och har ett gratis kroppsdiagram som följande:

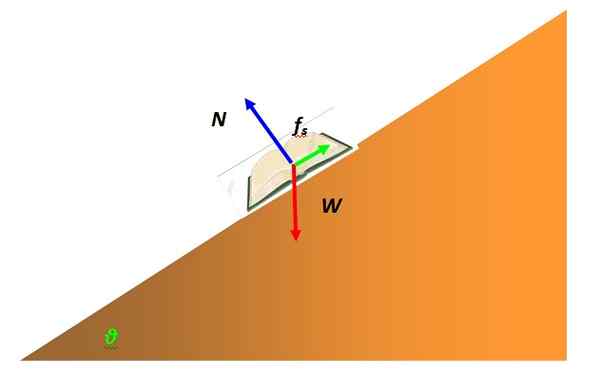Figur 4. Gratis kroppsdiagram över en bok på ett lutande plan. Källa: Självgjord.

Kraften som förhindrar att boken glider genom ytan på det lutande planet och förblir i vila är statisk friktion. Det beror på ytorna i kontakten, som mikroskopiskt har grovhet med toppar som är låsta, hindrar rörelse.

Det maximala statiska friktionsvärdet är proportionellt mot den normala kraften, som utövar ytan på det stödda objektet, men vinkelrätt mot nämnda yta. I exemplet med boken anges i blått. Matematiskt uttrycks det enligt följande:

F_Mer∝ N

Proportionalitetskonstanten är Statisk friktionskoefficient μ_s, vilket bestäms experimentellt, är dimensionslöst och beror på ytorna i kontakten i kontakt.

F_{S max} = μ_s N

Den dynamiska friktionen

Om en partikel är i dynamisk jämvikt sker rörelsen redan och statisk friktion ingriper inte mer. Om någon friktionskraft som motsätter sig rörelsen är närvarande, är de dynamiska friktionshandlingarna, vars storlek är konstant och ges av:

Kan tjäna dig: Vilka är de termiska egenskaperna och vad är det? (Med exempel)

F_k = μ_k N

Var μ_k Är han dynamisk friktionskoefficient, som också beror på vilken typ av ytor i kontakt. Liksom den statiska friktionskoefficienten är den dimensionlös och dess värde bestäms experimentellt.

Värdet på den dynamiska friktionskoefficienten är vanligtvis mindre än för statisk gnuggning.

Löst exempel

Boken i figur 3 är i vila och har en massa på 1.30 kg. Flygplanet har en lutningsvinkel på 30º. Hitta den statiska friktionskoefficienten mellan boken och planytan.

Lösning

Det är viktigt att välja ett lämpligt referenssystem, se följande figur:

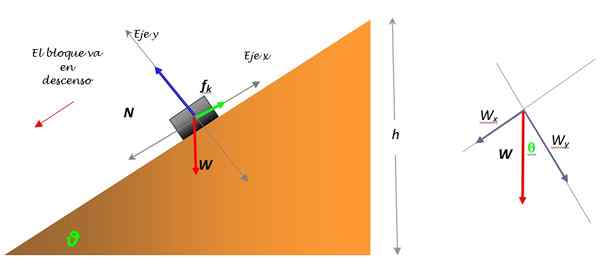Figur 5. Bok -fri kroppsdiagram på det lutande planet och nedbrytningen av vikt. Källa: Självgjord.

Bokens vikt har storlek W = mg, Det är dock nödvändigt att dela upp det i två komponenter: W_x och W_och, Eftersom det är den enda kraften som inte faller precis ovanför någon av koordinataxlarna. Nedbrytningen av vikt observeras i figuren till vänster.

W_och = mg.cosθ = 1.30 x 9.8 x cos 30º n = 11.03 n

W_x = mg.Senθ = 1.30 x 9.8 x Sen 30º = 6.37 n

Den andra. Newtons lag för den vertikala axeln är:

N - wy = 0

N = mg. cos θ = 11.03 n.

Tillämpa den 2: a. Newtons lag för X -axeln, som väljer som positiv riktningen för den möjliga rörelsen:

W_x - F_s = 0

Den maximala friktionen är F_{s max}= μ_sN, därför:

W_x - μ_sN = 0

μ_s = W_x / N = 6.37/11.03 = 0.58

Referenser

1. Rex, a. 2011. Fysikens grunder. Pearson. 76 - 90.
2. Serway, R., Jewett, J. (2008). Fysik för vetenskap och teknik. Volym 1. 7^ma. Ed. Cengage Learning. 120 - 124.
3. Serway, R., Vule, c. 2011. Fysikens grunder. 9^na Ed. Cengage Learning. 99-112.
4. Tippens, s. 2011. Fysik: koncept och applikationer. Sjunde upplagan. Macgraw Hill. 71 - 87.
5. Walker, J. 2010. Fysik. Addison Wesley. 148-164.