Vad är skärning, styvhet eller skjuvningsmodul? (Löst övningar)

han Klippa modul Beskriv ett materials svar på tillämpningen av en skjuvningsinsats som deformerar den. Andra frekventa valörer för skärmodulen är skjuv, sax, tvärgående elasticitet eller tangentiell elasticitetsmodul.

När ansträngningarna är små är deformationerna proportionella mot dem, enligt Hookes lag, varningskonstanten är proportionalitetskonstanten. Därför:

Cut Module = Cutting/Deformation Ansträngning

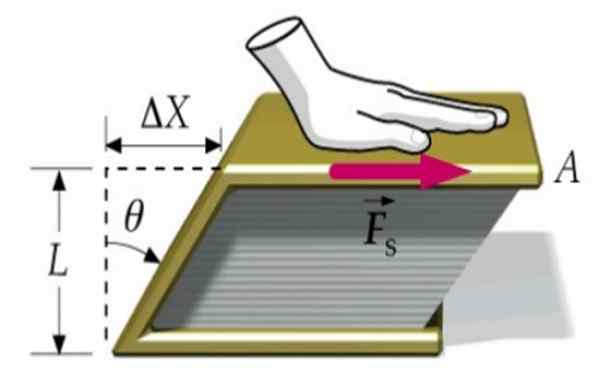
Figur 1. En bok deformeras tack vare Tangential Force FS. Källa: f. Zapata.

Anta att en kraft appliceras på locket på en bok, som är den andra fixerad på bordets yta. På detta sätt rör sig boken som helhet inte, men deformeras när det övre locket rör sig med avseende på den nedre i mängden Δx.

Boken går från att ha en rektangulär tvärsnitt till ett avsnitt i form av parallellogram, som vi ser i den överlägsna bilden.

Vara:

τ = f/a

Ansträngningen eller skärspänningen, att vara F storleken på den applicerade kraften och TILL Området som det agerar.

Deformationen orsakas av kvoten:

Δ = Δx / l

Därför är den skärande modulen, som vi kommer att beteckna som G,:

På detta sätt är skärningsmodulen ansvarig för att mäta motståndet i de inre planen för objektet som är parallellt med den tillämpade ansträngningen.

Och eftersom Δx / l saknar dimensioner, är enheterna i G desamma som de som är skärande ansträngningar, vilket är orsaken mellan kraften och området.

I det internationella enhetssystemet är dessa enheter Newton/Square Metro eller Pascal, förkortade PA. Och i Anglo -Saxon -enheter är det pund /kvadrat tum, förkortat psi.

[TOC]

Kan tjäna dig: enhetlig rätlinjig rörelse: egenskaper, formler, övningar

Skär modulen för olika material

Under handlingen av skärkrafter som de beskrivna erbjuder objekt ett motstånd som liknar bokens, där inre skikten glider. Denna typ av deformation kan endast förekomma i fasta kroppar, som har tillräcklig styvhet för att motsätta sig deformerade.

Å andra sidan erbjuder vätskor inte denna typ av motstånd, men de kan uppleva volymdeformationer.

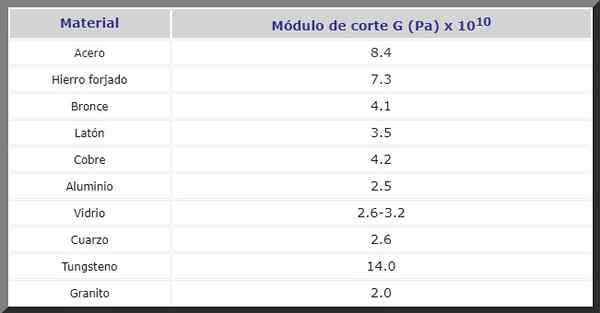
figur 2. Bultar i strukturer är föremål för skärningsinsatser. Källa: Pixnio.

Därefter har du g -cut -modulen i P för olika material som ofta används under konstruktion och vid tillverkning av maskiner och reservdelar av alla slag:

Experimentellt mått på skärmodulen

För att hitta värdet på skärmodulen måste du testa prover av varje material och undersöka ditt svar på tillämpningen av en skärningsinsats.

Provet är en stav tillverkad med materialet, med radio R och längd L känd, som är fixerad i ena änden, medan den andra ansluts till axeln på en fri remskiva.

Remskivan har ett rep bundet, vid vars fria ände en vägning hängs som utövar en kraft F På stången genom repet. Och denna kraft producerar i sin tur ett ögonblick M I stången, som sedan vänder en liten vinkel θ.

Ett monteringsschema kan ses i följande figur:

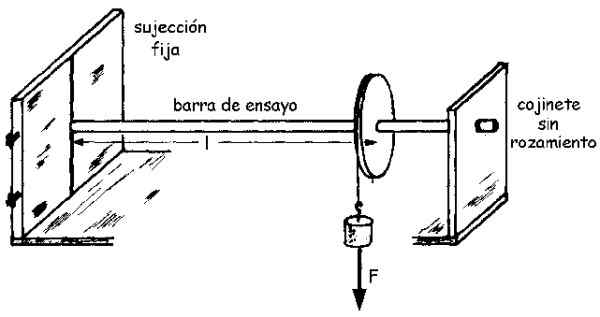Figur 3.- Experimentell montering för att bestämma skjuvmodulen eller skäret av en tunn teststång. Källa: University of Valladolid.

Ögonblickets storlek M, som vi betecknar som M (utan fet) är relaterad till vinkelroterad θ genom den klippta modulen G enligt följande ekvation (den dras av en enkel integral):

Eftersom ögonblickens storlek är lika med produkten från Force F -modulen med remskivans radie_p:

Det kan tjäna dig: Torricelli -experiment: Atmosfäriska tryckåtgärder, betydelse

M = f.R_p

Och kraft är den vikt som hänger W, så:

M = w.R_p

Ersätter i ekvationen i ögonblickets storlek:

Du har förhållandet mellan vikt och vinkel:

Hur man hittar g?

Detta förhållande mellan variabler W och θ Det är linjärt, så de olika vinklarna som hänger olika vikter mäts.

Par med vikt och vinkel är grafer på ett millimeterpapper, den bästa linjen som passerar genom de experimentella punkterna justeras och lutningen beräknas m av nämnda linje.

 Därifrån följer det:

Övningar med lösning

- Övning 1

En 2 -stav.5 meter lång och radio 4.5 mm är fixerad i ena änden. Den andra ansluter till en 75 cm radioskiva som har en 1 1 -vikt.3 kg. Den vända vinkeln är 9.Femte.

Med dessa data uppmanas att beräkna stångens klippmodul G.

Lösning

Från ekvationen:

Gasses G:

Och värdena som anges i uttalandet ersätts och är noga med att uttrycka alla uppgifter i det internationella enhetssystemet om:

R = 4.5 mm = 4.5 x 10 ^-3 m

R_p = 75 cm = 0.075

För att flytta från kilogram (de är faktiskt kilogram - kraft) till Newton multiplicerar med 9.8:

W = 1.3 kg-kraft = 1.3 x 9.8 n = 12.74 n

Och slutligen måste graderna vara på radianer:

9.5: e = 9.5 x2π /360 radianer = 0.1658 Radianes.

Med allt detta har du:

= 2.237 x 10¹⁰ Pa

- Övning 2

En gelkub är 30 cm sida. Ett av dess ansikten är fixerad, men samtidigt appliceras en parallell kraft på 1 n på motsatt ansikte, vilket tack vare detta rör sig 1 cm (se exemplet på boken i figur 1).

Det kan tjäna dig: Magnetisering: Orbital och snurrmagnetiskt ögonblick, exempel

Det uppmanas att beräkna med dessa data:

a) Skjuvspänningens storlek

b) enhetlig deformation Δ

c) Värdet på skärmodulen

Lösning till

Storleken på skjuvspänningen är:

τ = f/a

Med:

A = sida² = (30 x 10^-2 centimeter)² = 0.09 m²

Därför:

τ = 1 n / 0.09 m² = 11.1 pa

Lösning B

Enhet deformation är ingen annan än värdet på 5, ges av:

Δ = Δx / l

Förskjutningen av ansiktet som utsätts för kraften är 1 cm, då:

Δ = 1/30 = 0.0333

Lösning C

Skärmodulen och kvoten mellan skärningsansträngningen och enhetsdeformationen:

G = skärning/deformationsinsats

Därför:

G = 11.1 pa /0.033 = 336.4 PA

Referenser

1. Öl, f. 2010. Materialmekanik. McGraw Hill. Femte. Utgåva.
2. Franco Garcia, till. Stel. Hör modulmätning. Hämtad från: SC.Ehu.är.
3. Giancoli, D.  2006. Fysik: Principer med applikationer. Sjätte. Ed Prentice Hall.
4. Resnick, r. (1999). Fysisk. Vul. 1. 3: e upplagan. på spanska. Kontinentala redaktionella företag s.TILL. av C.V.
5. University of Valladolid. Department of Physics of Condensed Matter. Urval av problem. Återhämtat sig från: www4.druva.är.