Vad är det magnetiska ögonblicket?

han Magnetiskt ögonblick Det är en vektor som relaterar strömmen som korsar lite eller sluten slinga med det samma. Dess modul är lika med produkten från strömmen i området, och dess riktning och riktning ges av högerhandregeln, som visas i figur 1.

Denna definition är giltig oavsett. När det gäller enheten i det magnetiska ögonblicket, i det internationella enhetssystemet om det är Ampere × M².

Figur 1. Den magnetiska momentvektorn för en godtycklig strömbindning är vinkelrätt mot dess plan och riktningen bestäms av höger tumregel. Källa: Wikimedia Commons.

I matematiska termer, betecknar Vector Magnetic Moment med de grekiska texterna μ (I fetstil eftersom det är en vektor och därmed skiljer sig från dess storlek) uttrycks den som:

μ = Ia n

Där jag är intensiteten hos strömmen är A det område som omsluter slingan och n Det är enhetsvektorn (av modulen lika med 1) som pekar i riktningen vinkelrätt mot spasens plan, och vars betydelse ges av regeln om höger tumme (se figur 1).

Denna regel är mycket enkel: curling de fyra fingrarna på höger hand så att de följer strömmen, tummen indikerar riktning och riktning för n Och därför det magnetiska ögonblicket.

Den tidigare ekvationen är giltig för en slinga. Om det finns nougas som i en spole, multipliceras det magnetiska ögonblicket med N:

μ = nIa n

[TOC]

Magnetiskt ögonblick och magnetfält

Det är lätt att hitta uttryck för det magnetiska ögonblicket av varv med regelbundna geometriska former:

-Kvadratsidan av sidan ℓ: μ = Iℓ² n

-Sidor rektangulär spiral till och b: μ = Iab n

-Radio R. Radio Spira: μ = Iπr² n

Kan tjäna dig: atomnummer

Dipolos magnetfält

Magnetfältet som produceras av den aktuella slingan eller spasen liknar en stångmagnet och även jordens.

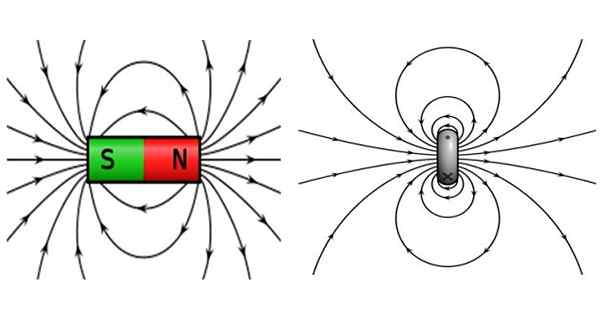figur 2. Till vänster magnetfältet på en stångmagnet och till höger som producerar en cirkulär spiral som transporterar ström. Källa: Wikimedia Commons.

Barmagneterna kännetecknas av att ha nordpol och sydpol, där motsatta poler lockas och samma poler avvisar. Fältlinjerna är stängda, lämna nordpolen och nå sydpolen.

Nu är de magnetiska polerna oskiljbara, vilket innebär att om en stångmagnet är uppdelad i två mindre magneter fortsätter de att ha sina egna nord- och sydpoler. Det är inte möjligt att ha de isolerade magnetiska polerna, varför stångmagneten kallas Magnetisk dipolo.

Magnetfältet för en radie r spiral r, som transporterar en ström i, beräknas av biot-savart-lagen. För de punkter som tillhör sin symmetriaxel (i detta fall X -axeln) ges fältet av:

Där μ_antingen Det är permeabiliteten hos vakuum. Att ta fältet på punkter bort från spasen, för vilket det uppfylls att x >> r, närmar sig fältet:

Förhållandet mellan magnetfältet och magnetmomentet för dipolo

Inklusive det magnetiska ögonblicket i det tidigare uttrycket är:

På detta sätt är magnetfältets intensitet proportionell mot det magnetiska ögonblicket. Observera att fältets intensitet minskar med distansbiten.

Detta tillvägagångssätt är tillämpligt på alla slinga, så länge som x vara stor jämfört med dess dimensioner.

Och eftersom linjerna i detta fält liknar stångmagneten, är ekvationen en bra modell för detta magnetfält och den för andra system vars linjer är lika, till exempel: till exempel:

Kan tjäna dig: absorbans: vad är, exempel och övningar löst

-Partiklar laddade i rörelse som elektron.

-Atomen.

-Jorden och andra planeter och satelliter i solsystemet.

-Stjärnstjärnor.

Effekt av ett externt fält på slingan

Ett mycket viktigt kännetecken för det magnetiska ögonblicket är dess länk till vridmomentet att loopupplevelsen i närvaro av ett yttre magnetfält.

En elmotor innehåller spolar genom vilka en ström av ändringsriktning går igenom och det tack vare den yttre fältupplevelsen en svängeffekt. Denna tur gör en axelrörelse och elektrisk energi blir mekanisk energi under processen.

Vridmoment på en rektangulär slinga

Anta att underlätta beräkningarna, en rektangulär sidor till och b, vars normala vektor n, Utgående skärm, initialt är den vinkelrätt mot ett enhetligt magnetfält B, Som i figur 3. Sidorna av Loop Experience -krafter som ges av:

F = JagL x B

Var L Det är en storleksvektor som är lika med segmentets längd och riktas enligt strömmen och är intensiteten för densamma och B Det är fältet. Kraften är vinkelrätt mot båda L Som fältet, men inte alla sidor upplever styrka.

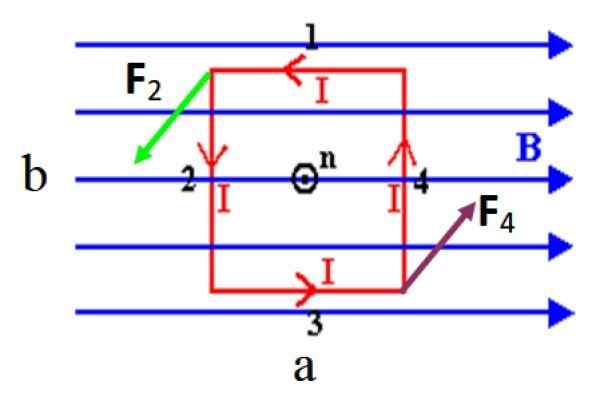Figur 3. En rektangulär spiral som transporterar en ström i i en anti -horary mening, upplever ett vridmoment i närvaro av ett enhetligt enhetligt magnetfält. Källa: f. Zapata.

I den visade figuren finns det ingen styrka på korta sidor 1 och 3 för att vara parallell med fältet, kom ihåg att tvärprodukten mellan parallella vektorer är ogiltiga. Men långa sidor 2 och 4, som är vinkelräta mot B, De upplever betecknade krafter som F₂ och F₄.

Dessa krafter bildas ett par: De har samma storlek och riktning, men motsatta sinnen, därför kan de inte flytta till slingan mitt i fältet. Men de kan få den att rotera, eftersom vridmomentet  τ Att varje kraft utövar, med avseende på den vertikala axeln som passerar genom slingans centrum, den har samma riktning och betydelse.

Kan tjäna dig: sammanhållningskraft

Enligt definitionen av vridmoment, var r Det är positionsvektorn:

τ = r x F

Så:

τ₂ = τ₄=(A/2) f (+J )

Enskilda vridmoment avbryts inte, eftersom de har samma riktning och mening, sedan läggs de till:

τ_netto = τ₂ + τ₄ = a f (+J )

Och som storleken på kraften F = IBB resulterar det:

τ_netto = I⋅A⋅B⋅B (+J )

A⋅B -produkten är område A i spasen, så IAB är storleken på det magnetiska ögonblicket μ. Därför τ_netto = μ⋅B (+J )

Det kan ses att vridmomentet i allmänhet sammanfaller med vektorprodukten mellan vektorerna μ och B:

τ_netto = μ x B

Och även om detta uttryck härstammar från en rektangulär slinga, är det giltigt för ett platt fotfäste godtyckligt.

Effekten av fältet på slingan är ett vridmoment som tenderar att anpassa det magnetiska ögonblicket till fältet.

Magnetdipolens potentiella energi

För att vända spiralen eller dipolen mitt i fältet måste ett verk utföras mot magnetkraften, som förändrar den potentiella energin i Dipolo. Variationen av energi ΔU, när spiralen roterar från vinkeln θ_antingen Vid vinkeln θ ges av integralen:

Om referensnivån väljs som θ_antingen = π/2:

ΔU = -μB cos θ

Som i sin tur kan uttryckas som skalprodukten mellan vektorerna B och μ:

ΔU = - μ ·B

Den minsta potentiella energin i dipolen inträffar när cos θ = 1, vilket betyder det μ och B De är parallella, energin är maximal om de är motsatta (θ = π) och är noll när de är vinkelräta (θ = π/2).

Referenser

1. Figueroa, D. 2005. Serie: Physics for Science and Engineering. Volym 5. Elektromagnetism. Redigerad av Douglas Figueroa (USB).
2. Resnick, r. 1999. Fysisk. Vul. 2. 3: e upplagan. på spanska. Kontinentala redaktionella företag s.TILL. av C.V.
3. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14th. Ed. Volym 2. Pearson.
4. Serway, R., Jewett, J. (2008). Fysik för vetenskap och teknik. Volym 2. 7th. Ed. Cengage Learning.
5. Tipler, s. (2006) Fysik för vetenskap och teknik. 5: e upplagan. Volym 2. Redaktör.