Vad är riktlinjen? (Geometri)

De direktiv I geometri består den av en kurva, yta eller volym som förblir fixerad och bestämmer hur ett geometriskt objekt bildas. Till exempel, av en linje, är andra kurvor som koniska, och revolutionytor, såsom den raka cirkulära cylindern etablerade.

Riktlinjekurvan kan också vara en omkrets. En rak cirkulär cylinder kan bildas genom att lämna en radie ri -r rión ri.

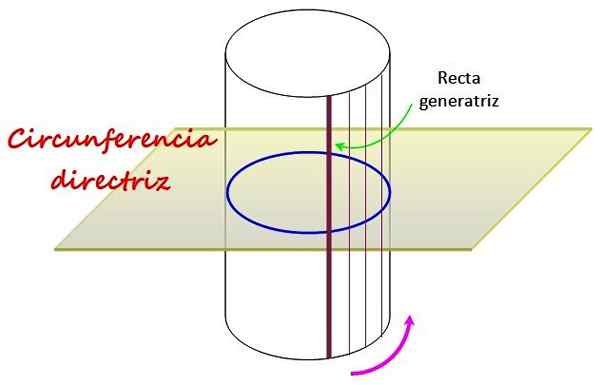
Figur 1. En rak cirkulär cylinder har som guide en cirkel, runt vilken en rak linje som heter Generatrix rör sig. Källa: f. Zapata.

Omkretsen, som är på planet ritat i figuren, bestämmer formen på den böjda ytan på den raka cirkulära cylindern, som genereras genom att rotera linjen runt den, kallad rak generatrix.

Om vägledningskurvan inte är en omkrets, utan en annan kurva, genereras andra typer av cylinder, till exempel den elliptiska cylindern, vars riktlinje är en ellips.

En omkrets kan också fungera som en riktlinje för att generera en annan kurva, så är fallet med Epitrokoid, En kurva i planet som genereras av en punkt, som i sin tur är i en mindre cirkel som rullar utan glid, runt riktlinjen.

Det är lättare att uppskatta det visuellt genom följande animation:

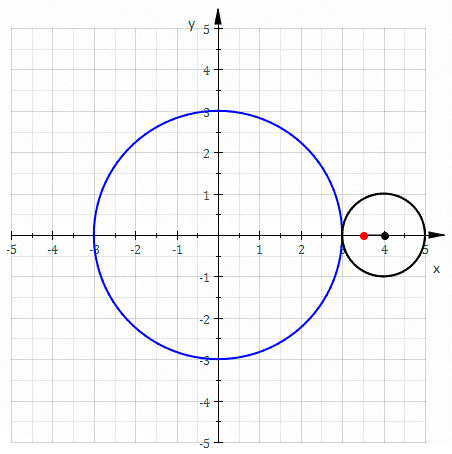figur 2. Den röda kurvan kallas Epitrocide och dess riktlinjekurva. Källa: Wikimedia Commons. Sam Derbyshire på den engelska Wikipedia/CC BY-S (http: // Creativecommons.Org/licenser/BY-SA/3.0/).

Riktlinjekurvan på cylindriska ytor

Cylindriska ytor klassificeras enligt deras riktlinjekurva i cylindrar:

-Cirkulär

-Elliptisk

-Parabolisk

-Hyperbolisk

När en cylindrisk yta har en riktlinje som ligger i ett plan vinkelrätt mot den för generatrixlinjen, är ekvationen för nämnda yta densamma som riktlinjen för riktlinjen.

Det kan tjäna dig: vad är förhållandet mellan rombområdet och rektangeln?

Cylindrarna tillhör gruppen av Fyrkantiga ytor, vars ekvation är andra klass med tre variabler. Den allmänna formen är:

Yxa² + Förbi² + Cz² + Dxy + exz + fyz + gx + hy + iz + k = 0

Där koefficienter a, b, c ... är verkliga siffror.

Cylindrarna är de vanligaste och användbara tre -dimensionella geometriska kropparna som kan hittas, särskilt de raka cirkulära cylindrarna, men de andra typerna av cylindrar som beskrivs nedan har också applikationer inom teknik och design.

Rak cirkulär cylinder

Dess riktlinje är en cirkel C som är i ett plan vinkelrätt mot cylindern, som visas i figur 1, eftersom generatrix -linjen, som går till C för att bilda sidoytan, är vinkelrätt mot C.

Ekvationen av omkrets C på XY -planet, fokuserat på ursprunget (0,0) är:

x² + och² = R²

Där r, kommer omkretsens radie uppenbarligen att vara cylinderns radie. Höjden H på cylindern sträcker sig längs Z -axeln, vinkelrätt mot XY -planet.

Elliptisk cylinder

Riktlinjen är en ellips i XY -planet centrerat på ursprunget (0,0), vars ekvation är:

Generatrix är en linje vinkelrätt mot XY -planet, som rör sig runt ellipsen för att ge upphov till sidoytan. Ellipsen kan vara i valfri höjd z på XY -planet.

Till exempel ekvationen ellipse:

4x² + 9y² = 36

Det är riktlinjekurvan som ger upphov till den elliptiska cylindern vars ekvation är 4x² + 9y² = 36, plus z = 0. Att lägga till detta sista uttryck är det tydligt att det är ytan.

Kan tjäna dig: provtagningsfel: formler och ekvationer, beräkning, exempel

Parabolcylinder

I detta fall är riktlinjen en liknelse, som kan vara av formen y = x². Således riktas cylindern längs z -axeln och bildar staplingsparabler med ett toppunkt i (0,0) längs den axeln.

Den paraboliska cylindern har applicering i solenergi, eftersom vissa samlare har speglar på det sättet, genom vilka solljus koncentreras i fokus. Denna punkt passerar ett rak rör inom vilket en olja når temperaturer upp till 400 ° C.

Hyperbolisk cylinder

I den hyperboliska cylindern är riktlinjens ekvation hyperbola centrerad på ursprunget:

Cylindern bildas till stacken.

Revolutionyta

Riktlinjekurvan för en revolutionyta är samma revolutionsaxel, linjen runt vilken kurvan som ansvarar för att generera ytan.

Kurvan som kretsar kan ha godtycklig form, på detta sätt genereras ett område som det ses i denna animering:

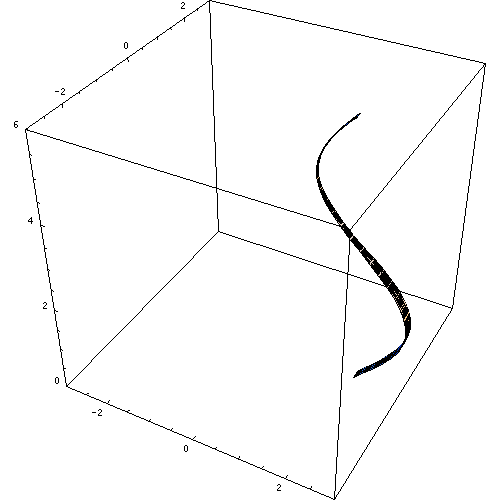Figur 3. En revolutionyta. Källa: Wikimedia Commons. https: // ladda upp.Wikimedia.Org/wikipedia/commons/e/e7/rotationskoerper_animation.GIF.

Om en annan rad vänds på riktlinjen erhålls den redan bekanta raka cirkulära cylindern. På samma sätt kan andra revolutionytor erhållas, såsom koniska, sfäriska och toroidala revolutionytor.

Konisk yta

En konisk yta genereras genom rörelse av en generatrixlinje som alltid passerar genom den fasta plana kurvan eller riktlinjekurvan och av den fasta punkten som kallas toppunkt, som inte tillhör riktlinjesplanet.

Kan tjäna dig: Matematiskt hopp: Formel, egenskaper, exempel, träning

Toppen eller spetsen delar konen i två delar, kallad löv antingen grenar.

Löst övningar

- Övning 1

Hitta det laterala området i den höga cirkulära cylindern med höjd 25 cm, vars riktlinjekurva är 6 cm radieomkrets, fokuserad på ursprunget.

Lösning

Cylinderns laterala område är produkten av riktlinjens längd efter höjd. Om R är omkretsens radie och H är cylinderns höjd, ges området av:

A = 2πr x h = 2πx 6 cm x 25 cm = 942.5 cm²

- Övning 2

Du har följande ekvation som motsvarar en quadric yta:

x² + och² + 2Z² +2xz - 2yz = 1

Ange vilken yta den är och vad som är riktlinjens ekvation.

Lösning

Gör z = k, där k är konstant, det erhålls:

x² + och² + 2K² +2kx - 2ky = 1

Vi ordnar om villkoren enligt följande:

(x² + 2kx) + (och²- 2ky) = 1-2k²

Rutor måste², För att inte förändra någon av parenteserna:

(x² + 2kx + k² - k² ) + (och² - 2ky + k² - k²) = 1-2K²

(x² + 2kx + k²) - k²  + (och²- 2ky + k²) - k² = 1-2K²

På detta sätt kvarstår det:

(x + k)² + (och - k)² = 1

Liksom ekvationen för en mittcirkel (-k, k) och radie 1, är ytan en rak cirkulär cylinder, även av radio 1, så länge generatrixlinjen är vinkelrätt mot nämnda omkrets.

Till exempel, med K = 0, reduceras ekvationen till omkretsen centrerad på ursprunget (0,0) vars radie är 1:

x² + och² = 1

Referenser

1. Gaussier. Representera tre dimensionella ytor. Återhämtat sig från: Gaussians.com.
2. Kindle, J. Teori och problem med analytisk geometri. McGraw Hill. Schaumserie.
3. Ytor som geometriska platser. Återhämtat sig från: algebra.Frlp.Utn.Edu.ar.
4. Suárez, m. Ytor. Hämtad från: ämnen.Unk.Edu.ar.
5. Fyrkantiga ytor. Återhämtat sig från: system.fciencias.Unk.mx.