Induktiv reaktans

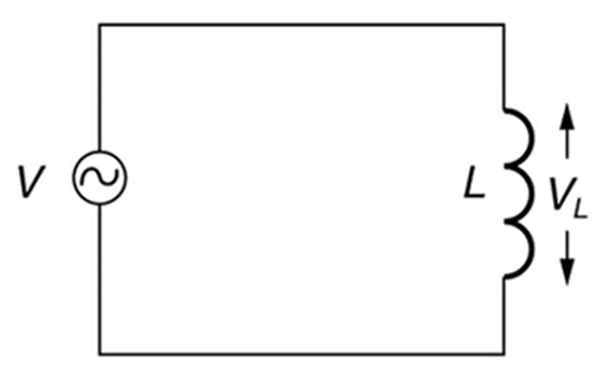
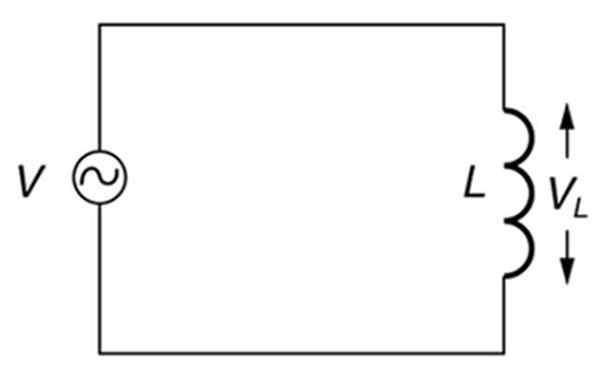En rent induktiv alternativ krets. Källa: Öppna Stax. Högskolefysik.

Vad är induktiv reaktans?

De Induktiv reaktans Den hänvisar till den opposition som presenteras av spolen till passagen av strömmen, i en alternativ krets. Med andra ord är det inducerarens förmåga att minska strömmen i en alternativ krets. Betecknas som x_L, Dess värde beror på induktansen och vinkelfrekvensen för spänningen:

X_L= Ω ∙ l

Där ω är vinkelfrekvensen i radianer/s och l induktans, mätt i Henrios (h) i det internationella enhetssystemet om.

Stora induktanser ger stor induktiv reaktans, eftersom deras motstånd mot förändring är större. Och reaktansen ökar också med frekvensen, så en viss induktans L kommer att ge större reaktans, desto högre spänningsfrekvens.

Den induktiva reaktansenheten är Ohmio, symboliserad av ω. Det är samma enhet av elektrisk motstånd, men till skillnad från detta, x_L Det är inte konstant, eftersom det beror på frekvensen för den alternativa spänningen.

I en krets vars enda element är en alternativ källa och en induktans (induktiv krets), såsom den som visas i figuren ovan, kommer den induktiva reaktansen att bero på källans frekvens.

Men Xs analogi_L Med elektrisk motstånd kan det utvidgas till den induktiva kretsen, vilket tillåter tillämpning av Ohms lag. Om x är definierad_L som förhållandet mellan spänningsamplituder V_L I induktorn och den nuvarande i_L Det korsar det:

X_L = V_L / Yo_L

Du kan skriva OHM -lagen för rent induktiva kretsar enligt följande:

V_L = X_L∙ i_L

Induktiv reaktansformler

För att beräkna den induktiva reaktansen används formeln som ges i början, där L representerar induktans (Henrios) och ω är vinkelfrekvensen (radianer/andra):

Kan tjäna dig: Millikan Experiment: Procedure, Förklaring, betydelse

X_L= Ω ∙ l

Det är vanligt att frekvensen uttrycks i Hertz eller Hertzio (HZ). I detta fall betecknas det med F och är relaterat till vinkelfrekvensen genom formeln:

Ω = 2π ∙ f

I detta fall beräknas reaktansen som:

X_L= 2πf ∙ l

I någon av dessa formler resulterar den induktiva reaktansen i ohm, som tidigare förklarats.

Effekten av induktans på en induktiv krets

Eftersom induktansen motsätter sig strömförändringarna eller variationerna i strömmen, kännetecknas den induktiva reaktansen av att försena strömvågen med avseende på spänningsvågen.

I följande graf, som visar spänning V_L (Blå) och den nuvarande i_L (röd) I induktorn, båda sinoidalt, observeras att båda vågorna är föråldrade 90º. Börjar vid t = 0 är spänningsvärdet maximalt, men strömmen är noll just nu.

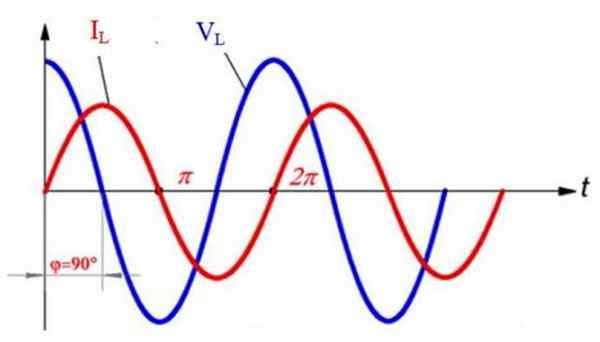Alternativ ström och spänning i en induktiv krets. Förberedd av: f. Zapata.

Senare observeras att strömmen når sitt maximala värde vid t = π /2, men då avbryts spänningen och investerar sin polaritet, det vill säga den blir negativ. Samtidigt minskar strömmen dess värde, medan spänningen blir mer och mer negativ.

Därefter, vid t = π, når spänningen sin maximala storlek, men med den inverterade polariteten, och sedan avbryts strömmen. Från allt detta följer det att när V_L Den når en topp, strömmen avbryts, och varje gång strömmen når sin maximala storlek är spänningen 0.

Strömmen når alltid sin topp efter spänningen, och detta beror på att, som anges i början, induktans motsätter sig eller minskar eller minskar.

Kan tjäna dig: Mekanisk fördel: Formel, ekvationer, beräkning och exempel

Hur man beräknar den induktiva reaktansen

Att beräkna den induktiva reaktansen är mycket enkel: det är nödvändigt att veta värdet på induktansen och frekvensen för den alternativa spänningen som appliceras. Sedan ersätts dessa data i en av de formler som anges i föregående avsnitt och motsvarande operation utförs.

Följande exempel och upplösta övningar visar hur man gör det i olika situationer.

Exempel

Exempel 1

Anta att en L = 5 MH -induktor, till vilken en alternativ frekvensspänning appliceras 60.0 Hz. Den induktiva reaktansen i detta fall beräknas av:

X_L= 2πf ∙ l

Men innan du ersätter värdena måste induktans bli Henrios, multiplicera med 1 × 10 -faktorn⁻³. Därför:

L = 5 × 10⁻³ H

Så:

X_L= 2πf ∙ l = x_L= 2π × 60 Hz × 5 × 10⁻³ H = 1. 88 ohm

Exempel 2

Nu är samma induktans ansluten till en annan alternativ frekvensspänning: 10.0 kHz. I detta fall presenterar induktans en större reaktans:

X_L= 2πf ∙ l = x_L= 2π × 10.0 × 10³ Hz × 5 × 10⁻³ H = 314.2 ohm

Exempel 3

Spänningen som appliceras på induktansen för exempel 1 och 2 har ett värde på 120 V rms. Den respektive RMS -strömmen bestäms genom OHM V -lag_L = X_L∙ i_L:

Yo_L = V_L / X_L

För frekvensen 60.0 Hz, strömmen är:

Yo_L = 120 V / 1. 88 ohm = 63.8 a

Och för frekvensen 10.0 kHz:

Yo_L = 120 V / 314.2 ohm = 0.38 a

Eftersom reaktansen i det senare fallet är mycket större förväntas att strömmen blir mindre. Den här egenskapen gör induktorn till ett högfrekvensfilter, en funktion som används för att minska högfrekvensljud i ljudutrustning eller för att skydda enheter från plötsliga nuvarande UPS, bland andra applikationer.

Kan tjäna dig: Steiner Theorem: Förklaring, applikationer, övningar

Löst övningar

Övning 1

Bestäm den induktiva reaktansen i en krets som består av en induktans på 2.5 MH, i serie med en alternativ spänningskälla, vars frekvens är 75 R.p.m.

Lösning

En fullständig revolution eller cykel är lika med 2π -radianer, och en minut har 60 sekunder, därför är en frekvens på 75 r.p.M motsvarar:

75 r.p.M = 75 × 2π radianer / 60 sekunder = 7.85 radianer/s

Och med detta värde är reaktansen:

X_L= Ω ∙ l = (7.85 radianer/s) × 2.5 × 10⁻³ H = 0.02 Ω

Övning 2

Seriell induktans används med källan till en dator för att filtrera bruset från höga frekvenser.

a) Vad ska vara det minsta induktansvärde som krävs för att producera en 2 kΩ reaktans, om frekvensen för signalen som är att filtrera är 15 kHz?

b) Hitta reaktansen hos denna induktor vid frekvensen 60 Hz.

Lösning till

X_L = 2 kΩ = 2000 Ω

F = 15 kHz = 15000 Hz

Därför rensning av ekvation x_L= 2πf ∙ l, du har:

L = x_L / 2π ∙ f = 2000 Ω / 2π × 15000 Hz = 0.0212 h = 21.2 MH

Lösning B

Använda x igen_L= 2πf ∙ l, men med f = 60 Hz, resultat:

X_L= 2π × 60 Hz × 0.0212 h = 8 ohm.

Referenser

1. Bauer, w. (2011). Fysik för teknik och vetenskap. Volym 1. MC Graw Hill. 
2. Giancoli, D. (2006). Fysik: Principer med applikationer. Sjätte. Ed Prentice Hall.
3.  Katz, D. (2013). Fysik för forskare och ingenjörer. Stiftelser och anslutningar. Cengage Learning.
4. Öppna stax. Högskolefysik. Hämtad från: OpenStax.org.
5. Sears, Z. (2016). Universitetsfysik med modern fysik. 14th. Ed. Volym 2. Pearson