Oblicual Rights Egenskaper, ekvationer och exempel

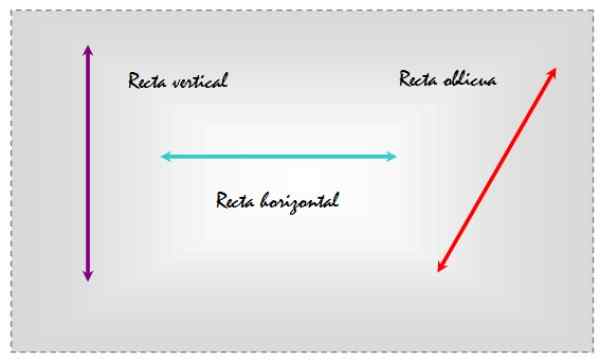
De snedda linjer De är de som är benägna, antingen med avseende på en plan yta eller en annan linje som indikerar en viss adress. Som ett exempel kan du överväga de tre linjerna som ritas i ett plan som visas i följande figur.

Vi känner till deras respektive relativa positioner eftersom vi jämför dem med en referenslinje, som vanligtvis är X -axel som betecknar horisontellt.

Figur 1. Vertikala, horisontella och sneda linjer i samma plan. Källa: f. Zapata.

På detta sätt, att välja den horisontella referensen, är den vänstra linjen vertikal, mitten är horisontellt och den till höger är sned, eftersom den är benägen med avseende på de dagliga referenslinjerna.

Nu upptar de linjer som finns på samma plan, till exempel ytan på papperet eller skärmen, olika positioner relativt varandra, beroende på om de korsar eller inte. I det första fallet är de torra raka, medan de i den andra är parallella.

Å andra sidan kan torklinjer också vara sneda eller vinkelräta raka linjer. I båda fallen är lutningarna i linjerna olika, men de sneda linjerna bildas bland sig α- och ß -vinklar, utom 90º, medan vinklarna bestäms av de vinkelräta linjerna är alltid 90º.

I följande figur sammanfattas dessa definitioner:

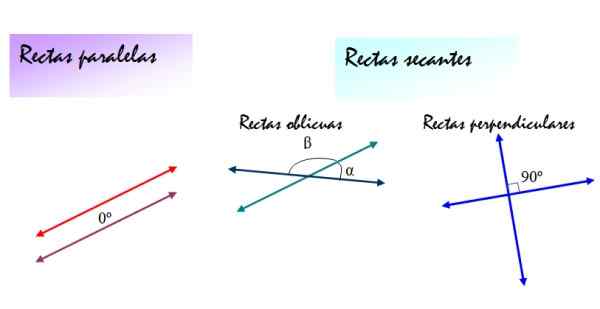figur 2. Relativa positioner mellan linjer: parallella, sned och vinkelräta skiljer sig åt i vinkeln som formar med varandra. Källa: f. Zapata.

[TOC]

Ekvationer

För att känna till de relativa positionerna för linjerna i planet är det nödvändigt att veta vinkeln som de bildar med varandra. Observera att raderna är:

Kan tjäna dig: Beräkning av tillvägagångssätt med skillnader

Parallell: Om de har samma lutning (lika riktning) och aldrig korsar varandra, så deras poäng är lika.

Slump: När alla deras poäng sammanfaller och därför har samma lutning, men avståndet mellan deras poäng är noll.

Secantes: Om dina örhängen är olika varierar avståndet mellan deras punkter och skärningspunkten är en enda punkt.

Så, ett sätt att veta om två linjer i planet är torrt eller parallellt är genom dess sluttning. Kriterierna för parallellitet och vinkelräthet för linjerna är följande:

Vara två rader l₁ och jag₂ tillhör ett plan, vars väntande är m₁ och M₂. Dessa linjer är parallella om m₁ = m₂ och de är vinkelräta när m₁= -1/m₂

Om vi ​​känner till sluttningarna av två rader i planet, inget av ovanstående kriterier är uppfyllda, drar vi slutsatsen att linjerna är sneda. Genom att känna till två punkter på en linje beräknas lutningen omedelbart, som vi kommer att se i nästa avsnitt.

Du kan ta reda på om två rader är torra eller parallella med att hitta sin korsning, lösa systemet med ekvationer som bildas: Om det finns en lösning är de torra, om det inte är de är parallella, men om lösningarna är oändliga är linjerna linjerna tillfällig.

Detta kriterium informerar emellertid inte om vinkeln mellan dessa linjer, även om de har skärningspunkt.

För att känna till vinkeln mellan linjerna behövs två vektorer eller och v som tillhör var och en av dem. Således är det möjligt att veta vinkeln som de bildar genom den skalära produkten från vektorerna, definierade på detta sätt:

eller•v =eller.v.cos a

Linjeekvation i planet

En linje i det kartesiska planet kan representeras på flera sätt, till exempel:

Det kan tjäna dig: allmän parabola -ekvation (exempel och övningar)

-I väntan på internment-formulär: Ja m Det är linjens lutning och b Det är skärningspunkten mellan linjen med den vertikala axeln, ekvationen för linjen är y = mx +b.

-Allmän ekvation för en rak linje: Ax + av + C = 0, var M = a/b Det är lutningen.

I det kartesiska planet är vertikala och horisontella linjer särskilda fall av linjekvationen.

-Vertikala linjer: x = a

-Horisontella linjer: y = k

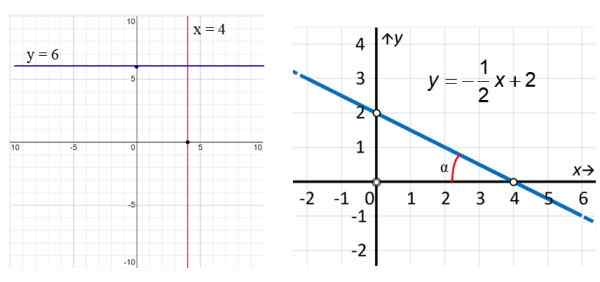Figur 3. Till vänster den vertikala linjen x = 4 och den horisontella linjen y = 6. Till höger ett exempel på sned linje. Källa: f. Zapata.

I exemplen på figur 3 har den vertikala röda linjen ekvation x = 4, medan linjen är parallell med x -axeln (blå) har ekvation y = 6. När det gäller rätt linje ser vi att den är sned och för att hitta dess ekvation använder vi punkterna som markeras i figuren: (0.2) och (4.0) på detta sätt:

M = (och₂ - och₁) / (X₂ - x₁) = (2 - 0) / (0 - 4) = - ½

Snittet av denna linje med den vertikala axeln är y = 2, Som nämnts från grafiken. Med denna information:

y = (-½) x+2

Att bestämma lutningsvinkeln med avseende på x -axeln är enkel. Jag känner att:

α = Arctg (2/4) = 26.Sjätte

Därför är den positiva vinkeln från X -axeln till linjen: 180º - 26.6: e = 153.4th

Exempel på sneda linjer

Figur 4. Exempel på sneda linjer. Källa: Ian Patterson Wrathful [CC av (https: // CreativeCommons.Org/licenser/av/2.0)]. PISA: s lutande torn. Pixabay.

Skulta linjer visas på många ställen, det handlar om att uppmärksamma att hitta dem i arkitektur, sport, ledning av elförsörjning, rör och på många fler ställen. I naturen är sneda linjer också närvarande, som vi kommer att se nedan:

Kan tjäna dig: härledningsregler (med exempel)

Ljusstrålar

Sol ljus sprids i en rak linje, men jordens rundade form påverkar hur solljus påverkar ytan.

På bilden nedan kan vi tydligt uppskatta att solstrålarna påverkar vinkelrätt i de tropiska regionerna, men istället anländer de snett till ytan i de tempererade regionerna och i polerna.

Därför reser solens strålar längre avstånd genom atmosfären och även värmen sprids på en större yta (se figur). Resultatet är att områden nära polerna är kallare.

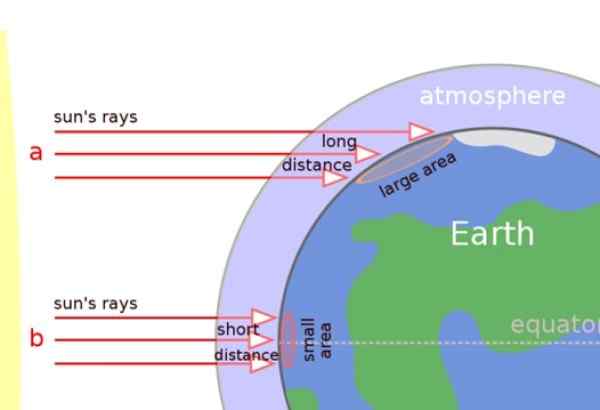Figur 5. Solens strålar påverkar snett de tempererade zonerna och polerna, men de är mer eller mindre vinkelräta i tropikerna. Källa: Wikimedia Commons.

Linjer som inte finns i samma plan

När två rader inte är i samma plan kan de fortfarande vara sned eller berömde, Som de också är kända. I det här fallet är dess styrelseledamöter inte parallella, men tillhör inte samma plan, dessa linjer har ingen skärningspunkt.

Till exempel är linjer i rätt figur tydligt i olika plan. Om de ser ovanifrån observeras att de effektivt korsar, men de har inte en gemensam punkt. Till höger ser vi cykelhjulen, vars strålar verkar korsa när de ser rakt framåt.

Figur 6. Sneda linjer som tillhör olika plan. Källa: Vänster f. Zapata, höger pixabay.

Referenser

1. Geometri. Vektorchef för en linje. Återhämtat från: Juanbragado.är.
2. Larson, r. 2006. Beräkning med analytisk geometri. 8th. Utgåva. McGraw Hill.
3. Matematik är ett spel. Linjer och vinklar. Återställt från: Juntadeandalucia.är.
4. Linjer som korsar. Återhämtat sig från: Teacheraltuna.com.
5. Villena, m. Analytisk geometri i R3. Hämtad från: Dspace.Espol.Edu.Ec.