Bravais nätverkskoncept, egenskaper, exempel, övningar

De Bravais Networks De är uppsättningen av fjorton tre -dimensionella enhetsceller där atomerna i en kristall. Dessa celler består av ett tre -dimensionellt arrangemang av punkter som bildar en grundstruktur som upprepas regelbundet i de tre rumsliga riktningarna.

Ursprunget till detta valör för grundläggande kristallina strukturer kommer från 1850, då Auguste Bravais visade att det bara finns 14 möjliga grundläggande tre -dimensionella enhetsceller som är möjliga.

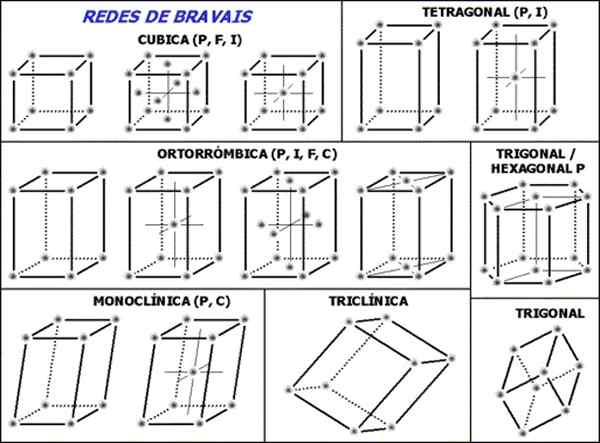
Figur 1. Bravais -nätverk är uppsättningen av de 14 nödvändiga och tillräckligt med enhetsceller för att beskriva alla kristallina strukturer. (Wikimedia Commons)

Uppsättningen av de 14 Bravais -nätverken är indelade i sju grupper eller strukturer enligt cellernas geometri, dessa sju grupper är:

1- Kubik

2- tetragonal

3- ortorrombisk

4- trigonal-hexagonal

5- monoklinisk

6- triklinisk

7- trigonal

Var och en av dessa strukturer definierar en enhetlig cell, detta är den minsta delen som behåller det geometriska arrangemanget av atomer i glaset.

[TOC]

Egenskaper för Bravais -nätverk

De fjorton näten av Bravais, som nämnts ovan, är indelade i sju grupper. Men var och en av dessa grupper har sina enhetsceller med sina karakteristiska parametrar som är:

1- Nätverksparametern (A, B, C)

2- Antal atomer per cell

3- Förhållande mellan nätverksparameter och atomradio

4- Koordinationsnummer

5- förpackningsfaktor

6- Interstitiella utrymmen

7- efter översättningar längs vektorer A, B, C Den kristallina strukturen upprepas.

Kubiknätverk

Det består av det enkla eller kubiska kubiska nätverket, kubiskt nätverk centrerat på ansikten eller kubiskt nätverk F och det kubiska nätverket centrerat på kubikkroppen eller nätverket.

Alla kubiska nätverk har de tre Nätverksparametrar motsvarande x, y -adresserna, z av samma värde:

A = b = c

Kubiskt nätverk s

Det är bekvämt att lyfta fram att atomer representeras av sfärer vars centra är i toppen av den kubiska cellen P.

Kan tjäna dig: konstgjorda satelliter

I fallet med det kubiska nätverket p antal atomer per cell Det är 1, för i varje toppunkt är bara den åttonde delen av atomen inuti enhetscellen, sedan 8*⅛ = 1.

han Samordningsnummer Anger antalet atomer som finns närliggande grannar i det kristallina nätverket. I fallet med det kubiska nätverket P är koordinationsnumret 6.

Kubiskt nätverk i

I denna typ av nätverk utöver atomerna i kubens toppar finns det en atom i mitten av kuben. Så atomnummer per cell Enhet i det kubiska nätverket P är 2 atomer.

figur 2. Kroppscentrerad kubiknätverk.

Kubiskt nätverk f

Det är det kubiska nätverket som utöver atomerna i vertikalerna har en atom i mitten av varje kub. han antal atomer per cell Det är 4, eftersom var och en av sex atomer i ansiktet har hälften inuti cellen är att säga 6*½ = 3 plus 8*⅛ = 1 i toppen.

Figur 3. Kubiskt nätverk centrerat på ansikten.

Hexagonalt nätverk

I detta fall är enhetscellen ett rak hexagonalt prisma. Hexagonala nätverk har de tre Nätverksparametrar motsvarande uppfyllande av följande förhållande:

A = b ≠ c

Att vara vinkeln mellan vektor A och B på 120º, som visas i figuren. Medan mellan vektorer A och C, såväl som mellan B och C är raka vinklar.

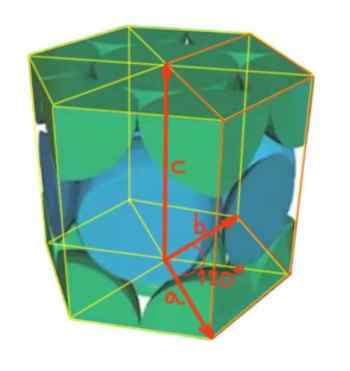Figur 4. Hexagonalt nätverk.

han antal atomer per cell Det kommer att beräknas enligt följande:

- I var och en av de två baserna i det hexagonala prismen finns 6 atomer i de sex vertikalerna. Var och en av dessa atomer upptar ⅙ av den enhetliga cellen.

- I mitten av var och en av de två hexagonala baserna finns en atom som upptar 1/2 enhetscell.

- På de 6 laterala ansikten av det hexagonala prismen finns det 3 atomer som var och en upptar ⅔ av enhetscellen och 3 atomer som upptar varje volym av enhetscellen.

Det kan tjäna dig: Hör Force: Surface and Mass Forces

(6 x ⅙) x 2 + ½ x 2 + ⅔ x 3 + ⅓ x 3 = 6 

Förhållandet mellan nätverksparametrar A och B med atomradie R under antagandet att alla atomer har lika radio och är i kontakt är: 

a/r = b/r = 2

Exempel

Metaller är de viktigaste exemplen på kristallina strukturer och också de enklaste eftersom de i allmänhet består av en enda typ av atom. Men det finns andra icke -metalliska föreningar som också bildar kristallina strukturer, såsom diamant, kvarts och många andra.

- Järnet

Järn har en enkel kubisk enhetscell med nätverksparameter eller kant a = 0,297 nm. I 1 mm finns det 3,48 x 10^6 enhetsceller.

- Koppar

Den har en kubisk kristallin struktur centrerad på ansikten, bildad endast av kopparatomer.

- Dyrbar ädelstenar

Precious ädelstenar är kristallina strukturer i princip samma förening, men med små delar av föroreningar som ofta är ansvariga för färgen på dem.

Diamant

Det består endast av kol och innehåller inte föroreningar, varför det saknar färg. Diamanten har Kubisk kristallisk struktur (Isometric-hexoctahedral) och är det svåraste kända materialet.

Kvarts

Den består av kiseldioxidoxid, den är vanligtvis färglös eller vit. Dess kristallina struktur är trigonal trapezoédrica.

Rubin 

Den består av aluminiumoxid med kromföroreningar som ger den dess karakteristiska röda färg. Bild en Hexagonalt kristallnätverk.

Safir 

Det är också en aluminiumoxidkristall, men med föroreningar av titan och järn, som är ansvariga för deras blå färg i olika nyanser. Som Ruby har sexkantig struktur.

Jade

Ädelsten generellt grönt, har Monoklinisk struktur Och det består av järn-magnesium-kalciosilikat.

Topas 

Det är färglöst med en Ortorrombisk struktur av aluminium-hydroxid-silikatfluorid.

Löst övningar

Övning 1

Hitta förhållandet mellan nätverksparametern och atomradie för ett kubiskt nätverk f.

Det kan tjäna dig: Theory of the Big Bang: Egenskaper, stadier, bevis, problem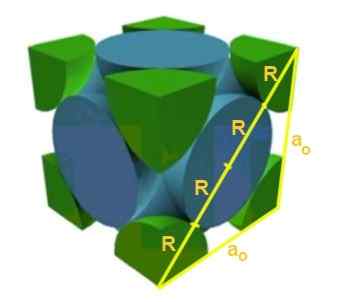

Lösning: För det första antas det att atomer representeras som sfärer alla radier r i "kontakt" med varandra, som visas i figuren. En rektangel triangel bildas där den uppfylls att:

(4 r)^2 = a^2 + a^2 = 2 a^2

Så du har att förhållandet mellan kantradio är:

A/R = 4/√2

Övning 2

Hitta förhållandet mellan nätverksparametern och atomradie för ett kubiskt nätverk I (kroppscentrerat).

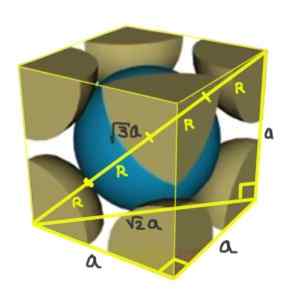
Lösning: Atomer är tänkta att representeras som alla radie R -sfärer i "kontakt" med varandra, som visas i figuren.

Två rektanglar bildas en av hypotenusa √2a och den andra av hypotenus √3a som kan demonstreras med hjälp av Pythagorean Theorem. Därifrån måste du samband mellan nätverksparametern och atomradie för ett kubiskt nätverk I (centrerat i kroppen) är:

A/R = 4/√3

Övning 3

Hitta förpackningsfaktorn F för en enhetscell med en kubisk struktur F (kubikcentrerad på ansikten) där atomer har radio R och är i "kontakt".

Lösning: Förpackningsfaktorn F definieras som förhållandet mellan den volym som upptar av atomerna i enhetscellen och cellens volym:

F = vatomer / Vcell

Som visas ovan är antalet atomer per enhetscell i ett kubiskt nätverk centrerat på ansikten 4, så att förpackningsfaktorn kommer att vara:

F = 4 [4πr^3/3] /[a^3] = ..

... 4 [4πr^3/3]/[4r/√2]^3 = (√2) π/6 = 0,74

Referenser

1. Crystal Structures Academic Resource Center. [Pdf]. Hämtad den 24 maj 2018, från: webben.jag det.Edu
2. Kristaller. Hämtad den 26 maj 2018, från: Thoughtco.com
3. Pressböcker. 10.6 Latice -strukturer i kristallina fasta ämnen. Hämtad 26 maj 2018, från: OpenTextbc.Växelström
4. Ming. (30 juni 2015). Typer kristallstrukturer. Hämtad den 26 maj 2018, från: Crystalvisions-film.com
5. Helmestine, Anne Marie, PH.D. (31 januari 2018). Typer av 
6. Kittel Charles (2013) Solid State Physics, Condensed Matter Physics (8th Edition). Wiley.
7. Khi. (2007). Kristallstrukturer. Hämtad den 26 maj 2018, från: Folk.Ntnu.Nej
8. Wikipedia. Bravais latices. Hämtad från: i.Wikipedia.com.