Konvex polygondefinition, element, egenskaper, exempel

En konvex polygon Det är en geometrisk figur som finns i ett plan som kännetecknas eftersom det har alla dess diagonaler inuti och dess vinklar mäter mindre än 180º. Bland dess egenskaper är följande:

1) Den består av n på varandra följande segment där den sista av segmenten går med i den första. 2) Inget av segmenten korsas på ett sådant sätt som avgränsar planet i en inre och en annan yttre. 3) Var och en av vinklarna i det inre regionen är strikt lägre än en platt vinkel.

Figur 1. Polygoner 1, 2 och 6 är konvexa. (Förberedd av Ricardo Pérez).

Ett enkelt sätt att avgöra om en polygon är konvex eller inte ska överväga linjen som passerar genom en av dess sidor, som bestämmer två semiplaner. Om på varje linje som passerar å ena sidan, de andra sidorna av polygonen är i samma semiplane, är det då en konvex polygon.

[TOC]

Element i en polygon

Varje polygon består av följande element:

- Sidor

- Häckar

Sidorna är var och en av de på varandra följande segmenten som utgör polygonen. I en polygon kan ingen av de segment som utgör det ha en öppen ände, i så fall skulle det finnas en polygonal linje men inte en polygon.

Vertikalerna är unionspunkterna för två på varandra följande segment. I en polygon är antalet vertikaler alltid lika med antalet sidor.

Om två sidor eller segment av ett polygonkors, har du en korspolygon. Korsningspunkten betraktas inte som ett toppunkt. En korspolygon är en icke-konvex polygon. De kraschade polygonerna är korsade polygoner och är därför inte konvexa.

Det kan tjäna dig: analytisk geometri

När en polygon har alla sidor av samma längd finns det då en vanlig polygon. Alla vanliga polygoner är konvexa. 

Konvex och icke-konvexa polygoner

Figur 1 visar flera polygoner, några av dem är konvexa och andra är inte. Låt oss analysera dem:

Nummer 1 är en tresidig polygon (triangel) och alla inre vinklar är mindre än 180º, därför är det en konvex polygon. Alla trianglar är konvexa polygoner.

Numret 2 är en fyrsidig polygon (fyrkantig) där ingen av sidorna avlyssnas och även var och en av de inre vinklarna är mindre än 180º. Det är då en fyrsidig konvex polygon (konvex fyrkantig).

Å andra sidan är nummer 3 en fyrsidig polygon men en av dess inre vinklar är större än 180º, så den uppfyller inte konvexitetstillståndet. Det vill säga, det är en icke-konvex-sidig polygon som kallas en konkav fyrkantig.

Nummer 4 är en fyra -segment (sidor) polygon, varav två är avlyssna. De fyra inre vinklarna är mindre än 180 °, men när två sidor korsar är de en icke-konvexa korspolygon (korskvadrilateral).

Ett annat fall är nummer 5. Detta är en femsidig polygon, men eftersom en av dess inre vinklar är större än 180º, finns det då en konkav polygon.

Slutligen har nummer 6, som också har fem sidor, alla sina inre vinklar mindre än 180º, så det är en femsidig konvex polygon (konvex Pentagon).

Kan tjäna dig: provtagningsfel: formler och ekvationer, beräkning, exempel

Konvexa polygonegenskaper

1- En icke-crushed polygon eller enkel polygon delar upp planet som innehåller det i två regioner. Den inre regionen och den yttre regionen, som är polygonen gränsen mellan de två regionerna.

Men om polygonen dessutom är konvex, finns det en inre region som helt enkelt är besläktad, vilket innebär att man tar två punkter i det inre regionen, den alltid kan förenas med ett segment som tillhör i sin helhet till det inre regionen.

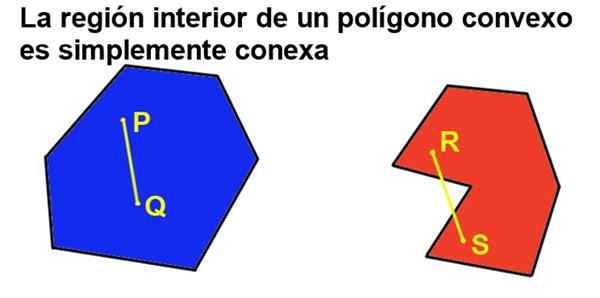figur 2. En konvex polygon är helt enkelt besläktad, medan en konkav inte är. (Förberedd av Ricardo Pérez).

2- All inre vinkel på en konvex polygon är mindre än en platt vinkel (180º).

3- Alla inre punkter i en konvex polygon tillhör alltid en av de halvdefinierade av linjen som passerar genom två på varandra följande vertikaler.

4- I en konvex polygon finns alla diagonaler fullt ut i det inre polygonområdet.

5- De inre punkterna i en konvex polygon tillhör i sin helhet till den konvexa vinkelsektorn som definieras av varje inre vinkel.

6- Varje polygon där alla dess vertikaler är på en omkrets är en konvex polygon som kallas cyklisk polygon.

7- Varje cyklisk polygon är konvex, men inte varje konvex polygon är cyklisk.

8- Varje icke-crushed polygon (enkel polygon) som har alla sidor av lika lång längd är konvex och kallas vanlig polygon.

Diagonaler och vinklar i konvexa polygoner

9- Det totala antalet diagonaler i en konvex polygon av N-sidor ges av följande formel:

Det kan tjäna dig: polybal grafik

N = ½ n (n - 3)

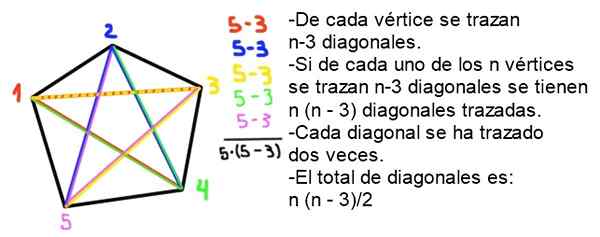
Demonstration: I en konvex polygon av N -sidor av varje toppunkt dras n - 3 diagonaler, eftersom själva toppen och de två angränsande är uteslutna. Eftersom det finns n vertikaler dras de totalt n - 2) diagonaler, men varje diagonal ritades två gånger, så antalet diagonaler (utan upprepning) är n (n -2)/2.

10- Summan av de inre vinklarna i en konvex polygon av N-sidor ges av följande förhållande:

S = (n - 2) 180º

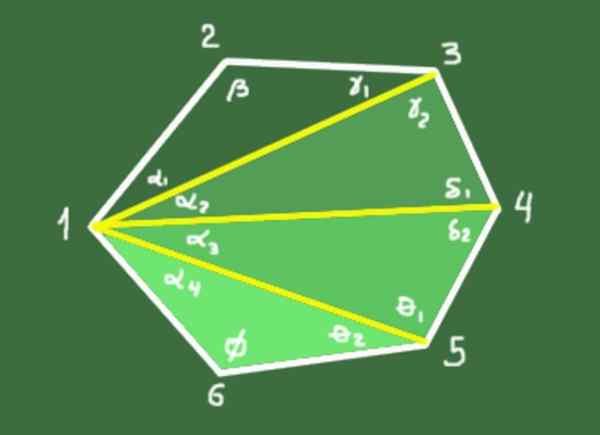
Demonstration: N-3-diagonaler dras från ett toppunkt som definierar N-2-trianglar. Summan av de inre vinklarna i varje triangel är 180º. Den totala summan av N-2-trianglarna är (N-2)*180º, som sammanfaller med summan av polygonens inre vinklar.

Exempel

Exempel 1

Cyklisk hexagon, det är en sexsidig polygon och sex vertikaler, men alla vertikaler är på samma omkrets. All cyklisk polygon är konvex.

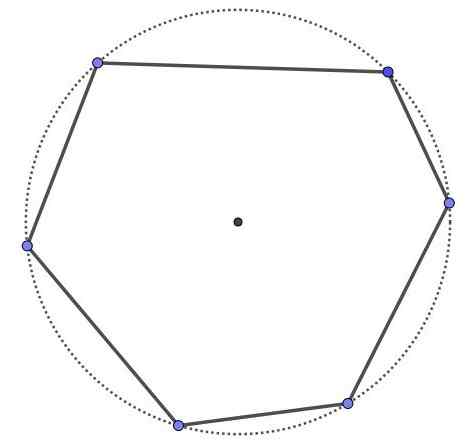Cyklisk hexagon.

Exempel 2

Bestäm värdet på de inre vinklarna på en vanlig ENEGON.

Lösning: Enegon är en 9 -sidad polygon, men den reglerar också alla sidor och vinklar är desamma.

Summan av alla inre vinklar på en 9 -sidad polygon är:

S = (9 - 2) 180º = 7 * 180º = 1260º 

Men det finns 9 inre vinklar med lika mått α, så följande jämlikhet måste uppfyllas:

S = 9 α = 1260º

Varifrån det följer att a -måttet på varje inre vinkel på den vanliga ENEGON är:

α = 1260º/9 = 140º