Newtons andra lagapplikationer, experiment och övningar

De Andra lagen i Newton o Grundläggande lagen i dynamiken konstaterar att om ett objekt är föremål för en kraft eller en uppsättning krafter som inte upphävs, kommer objektet att accelerera i riktning mot den resulterande kraften, att vara att accelerationen proportionell mot intensiteten hos den nettokraften och omvänt proportionell mot objektets massa.

Ja F är nettokraften, M Objektets massa och till Accelerationen han förvärvar, då skulle Newtons andra lag uttryckas matematiskt: till = F / M eller på det vanligaste sättet F = M∙till

Förklaring av Newtons andra lag. Källa: Självgjord.

[TOC]

Förklaring och formler

Som förklarats ovan är det vanliga sättet att uttrycka den andra lagen med formeln:

F = M∙till

Både acceleration och kraft måste mätas från ett tröghetsreferenssystem. Observera att massan är en positiv mängd, så accelerationen pekar i samma riktning som den resulterande kraften.

Observera också att när den resulterande kraften är ogiltig (F = 0) Då kommer accelerationen också att bli ogiltig ( till = 0 ) så länge som M> 0. Detta resultat är helt överens med Newtons första lag eller tröghetslag.

Newtons första lag upprättar tröghetsreferenssystem som de som rör sig med konstant hastighet med avseende på en fri partikel. I praktiken och för de vanligaste applikationerna kommer ett fast referenssystem till marken eller någon annan som rör sig med konstant hastighet med avseende på det, att övervägas tröghet.

Kraft är det matematiska uttrycket för samspelet mellan objektet med miljön. Kraft kan vara en konstant mängd eller förändring med objektets tid, position och hastighet.

Enheten i det internationella systemet (SI) för Force är Newton (N). Massan i (Si) mäts i (kg) och acceleration i (m/s²). En Newton av styrka är den nödvändiga kraften för att påskynda ett objekt på 1 kg massa vid 1 m/s² .

Löst övningar

Övning 1

Ett objekt med massa M frigörs från en viss höjd och en acceleration av fall på 9,8 m/s² mäts.

Detsamma gäller för en annan massa massa m 'och en annan av massa m "och en annan. Resultatet är alltid tyngdkraften som betecknas med G och är värd 9,8 m/s². I dessa experiment är formen på objektet och värdet på dess massa sådan att kraften på grund av luftmotstånd är försumbar.

Kan tjäna dig: kalciumfluorid (CAF2): struktur, egenskaper, användningar

Det uppmanas att hitta en modell för den markbundna attraktionskraften (känd som vikt) som överensstämmer med experimentella resultat.

Lösning

Vi valde ett tröghetsreferenssystem (fixat med avseende på golvet) med en positiv riktning för den vertikala X -axeln och ner.

Den enda kraften som verkar på massobjektet m Det är den markbundna attraktionen, den kraften kallas vikten P, hur det pekar ner är positivt.

Accelerationen som förvärvats av massobjektet m När den släpps är är a = g , Tary ner och positivt.

Vi föreslår Newtons andra lag

P = m a

Vad kommer att vara P -modellen så att den acceleration som förutses av den andra lagen är G oavsett värdet på M ? : Det enda alternativet är att p = m g varje gång m> 0.

m g = m a Där vi rensar: a = g

Vi drar slutsatsen att vikten, kraften med vilken jorden lockar ett objekt kommer att vara massan för objektet multiplicerat med tyngdens acceleration och dess riktning är vertikal och riktad.

P = m∙g

Övning 2

Ett 2 kg block av massa vilar på ett helt smidigt och horisontellt golv. Om en 1 n -kraft tillämpas som acceleration förvärvar blocket och vilken hastighet kommer att vara efter 1 s.

Lösning

Det första är att definiera ett tröghetskoordinatsystem. En har valts med X -axeln på golvet och axeln och vinkelrätt mot den. Sedan tillverkas ett kraftdiagram och placerar krafterna på grund av blockens interaktioner med omgivningen.

Kraften P representerar vikten, kraften med vilken planeten jorden lockar till sig Mass M.

Kraften n representerar det normala, det är den uppåt kraft som golvet ytan utövar på blocket m. Det är känt att n balanserar exakt till p eftersom blocket inte rör sig i vertikal riktning.

F är den horisontella kraften som appliceras för att blockera M, som pekar i den positiva riktningen för X -axeln.

Nettokraften är summan av alla krafter på massan M. Sumvektorn för F, P och N görs. Eftersom p och n är desamma och motsatta avbryter de varandra, och nettokraften är f.

Så att den resulterande accelerationen kommer att vara kvoten på nettokraften mellan massan:

Kan tjäna dig: Mekanisk fördel: Formel, ekvationer, beräkning och exempel

a = f / m = 1 n / 2 kg = 0,5 m / s²

När blocket börjar från resten efter 1s kommer dess hastighet att ha förändrats 0 m/s vid 0,5 m/s .

Newtons andra lagapplikationer

Accelerationen av en hiss

En pojke använder ett badrum för att mäta sin vikt. Värdet du får är 50 kg. Då tar pojken vikten av hissen i sin byggnad, eftersom han vill mäta accelerationen av hissstarten. Resultaten som erhålls när det startar är:

• Skalan registrerar en vikt på 58 kg under 1,5 s
• Mät sedan 50 kg igen.

Beräkna hissens acceleration med dessa data.

Lösning

Skalan mäter vikten i en enhet som heter Kilogram_fuerza. Per definition är kilogram_fuerza den kraft som planeten jorden lockar ett objekt på 1 kg massan.

När den enda kraften som verkar på objektet är dess vikt, får den en acceleration på 9,8 m/s². Så 1 kg_f motsvarar 9.8 n.

Vikten P av pojken är då 50 kg*9.8m/s² = 490 n

Under accelerationen utövar skalan en kraft N På pojken 58 kg_f motsvarande 58 kg * 9,8 m/s² = 568.4 n.

Accelerationen av hissen kommer att ges av:

A = n/m - g = 568.4 n / 50 kg - 9.8 m/s² = 1.57 m/s²

Hastigheten som förvärvats av hissen efter 1.5 s med 1 acceleration.57 m/s² är:

v = a * t = 1.57 m/s² * 1.5 s = 2.36 m/s = 8.5 km/h

Följande figur visar ett schema för krafterna som agerar på pojken:

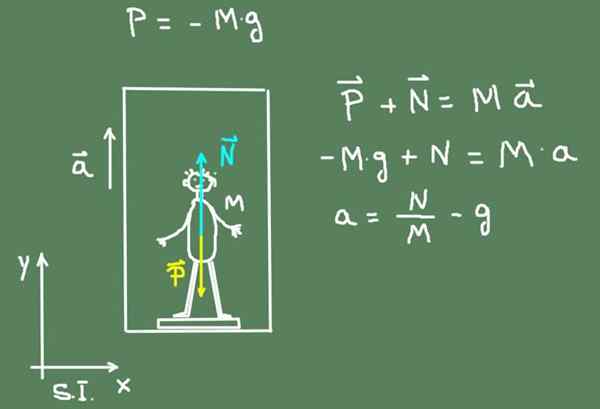
Majonnäsflaskan

Ett barn skickar sin brors flaska till sin bror, som är i andra änden av bordet. För det driver det det på ett sådant sätt att det förvärvar en hastighet av 3 m/s. Eftersom flaskan släpps tills den stannar i motsatt ände av bordet var rutten 1,5 m.

Bestäm värdet på friktionskraften som bordet utövar på flaskan och vet att den har en massa på 0,45 kg.

Lösning

Först kommer vi att bestämma bromsacceleration. För detta kommer vi att använda följande förhållande, som redan är kända för den enhetligt accelererade rätlinjiga rörelsen:

VF² = vi² + 2 * A * D

var Vf är den sista hastigheten, Fick syn på Den första hastigheten, till acceleration och d Förskjutningen.

Kan tjäna dig: dynamisk el

Accelerationen som erhållits från det tidigare förhållandet är, där förflyttningen av flaskan har tagits som positiv.

A = (0 - 9 (m / s) ²) / (2*1.5 m) = -3 m/s²

Nettokraften på majonnäsflaskan är friktionskraften, eftersom flaskans normala och vikt är balanserad: fnet = kallt.

Fr = m * a = 0.45 kg * (-3 m/s²) = -1.35 n = -0.14 kg-f

Barns experiment

Barn och vuxna kan också utföra enkla upplevelser som gör att de kan verifiera att Newtons andra lag verkligen fungerar i verkliga livet. Här är två intressanta bra:

Experiment 1

Ett enkelt experiment kräver badrum och hiss. Ta en badrumsvikt till en hiss och registrera värdena som markerar under stigningen, startstarten och under den period som rör sig med konstant hastighet. Beräkna accelerationerna för hissen som motsvarar varje fall.

Experiment 2

1. Ta en leksaksvagn som har dina hjul väl smörjade
2. Håll ett rep till det extrema.
3. Säkra en penna eller ett annat cylindriskt och smidigt föremål på kanten på bordet.
4. I den andra änden av repet hänger en liten korg, till vilken den kommer att placera några mynt eller något som tjänar för vikt.

Experimentschemat visas nedan:

• Släpp vagnen och observera hur den accelererar.
• Öka sedan vagnens massa genom att placera mynt på den, eller något som ökar dess massa.
• Säg om accelerationen ökar eller minskar. Placera mer deg på vagnen, observera hur den accelererar och avslutas.

Sedan är vagnen kvar utan extra vikt och låt den accelerera. Sedan placeras mer vikt på korgen för att öka kraften som appliceras på vagnen.

• Jämför accelerationen med föregående fall, ange om det ökar eller minskar. Du kan upprepa att lägga till mer vikt i korgen och observera accelerationen av vagnen.
• Ange om det ökar eller minskar.
• Analysera dina resultat och säga om de håller med Newtons andra lag eller inte.

Intresseartiklar

Exempel på Newtons andra lag.

Newtons första lag.

Exempel på Newtons andra lag.

Referenser

1. Alonso m., Finn e. 1970. Fysikvolym I: Mekanik. Inter -American Education Fund S.TILL. 156-163.
2. Hewitt, s. 2012. Konceptuell fysisk vetenskap. Femte upplagan. 41-46.
3. Young, Hugh. 2015. Universitetsfysik med modern fysik. 14: e upplagan. Pearson. 108-115.