Koniska avsnittstyper, applikationer, exempel

De koniska avsnitt De är de kurvor som erhålls genom att avlyssna ett plan med en kon. Det finns flera sätt att göra detta; Till exempel, om planet överförs vinkelrätt till konens axiella axel erhålls en omkrets.

Lutning av planet lite med avseende på konens axiella axel erhålls en ellips, en kurva som är stängd, men om vi lutar det ännu mer en parabola eller en hyperbola erhålls, som kan ses i animeringen av figur 1.

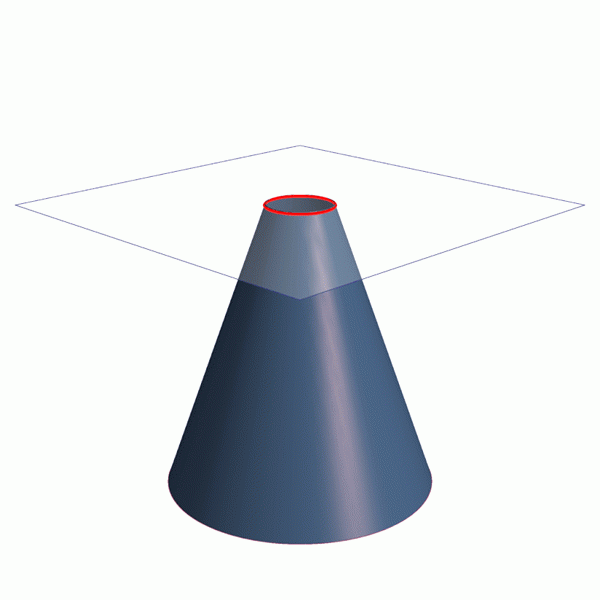Animering som visar hur man får de fyra koniska avsnitten: omkrets, liknelse och hyperbola ellips. Källa: Wikimedia Commons. Linjer / cc0

De koniska avsnitten är en del av naturen och världen runt oss. Teknik, arkitektur och astronomi är viktiga kunskapsgrenar som använder koniker.

[TOC]

Förhållanden för koniska avsnitt

De koniska sektionerna definieras som geometriska platser som uppfyller följande villkor:

Liknelse

Det är den geometriska platsen för alla punkter som ligger i ett likvidistiskt plan till en fast punkt som heter fokus F och en rak linje också fixad, kallad direktiv.

Ellips

En planpunkt tillhör en ellips om summan av avståndet mellan den punkten och två andra fasta punkter, kallas Focos och ligger på huvudaxel av ellipsen förblir konstant.

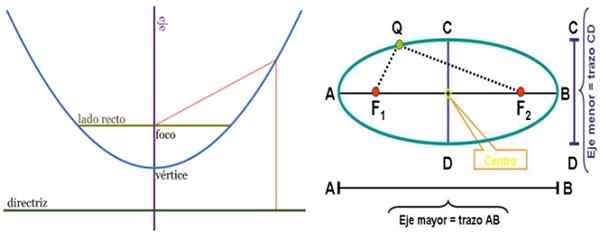Liknelsen till vänster och ellips till höger, med sina respektive element. Focierna är punkter med många applikationer. Källa: Wikimedia Commons.

Omkrets

Det är den geometriska platsen för alla punkter som upprätthåller samma avstånd till en annan punkt som heter Centro. Detta avstånd är radio av omkretsen.

Kan tjäna dig: euklidisk avstånd: koncept, formel, beräkning, exempel

Hyperbel

Uppsättning punkter i planet så att skillnaden mellan dess avstånd till två fasta punkter som kallas Focos, det är konstant.

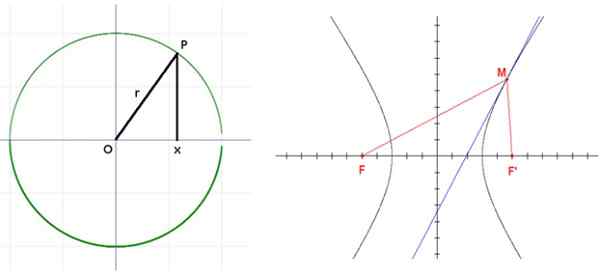Hyperbola med foci f och f. Källa: Wikimedia Commons.

Ansökningar

Låt oss titta på några av de koniska avsnitten Applications:

Liknelser  

-När ett objekt lanseras har banan som följer en liknelsform.

-Liknelserna har anmärkningsvärda tekniska applikationer, till exempel i de avstängda broarna kan kablarna skynda sig i form av liknelser.

-Liknelserna är också bra att göra reflektorer och teleskop. Detta är tack vare en intressant egenskap: När du placerar en armatur i fokus för en parabolisk tvärgående sektionsyta kommer ljuset att resa i parallella strålar till liknelssaxeln.

-Om de lysande strålarna är parallella med symmetri -axeln närmar sig den paraboliska ytan, koncentrerar den dem i fokus, en omständighet som används för att göra reflektorteleskop, såsom Hale de Monte Palomar -teleskopet.

Ellips

-Planeterna i solsystemet rör sig efter elliptiska banor, ganska nära omkretsen i fallet med de stora planeterna, inkluderade landet. Solen är inte i mitten, utan i en av strålkastarna.

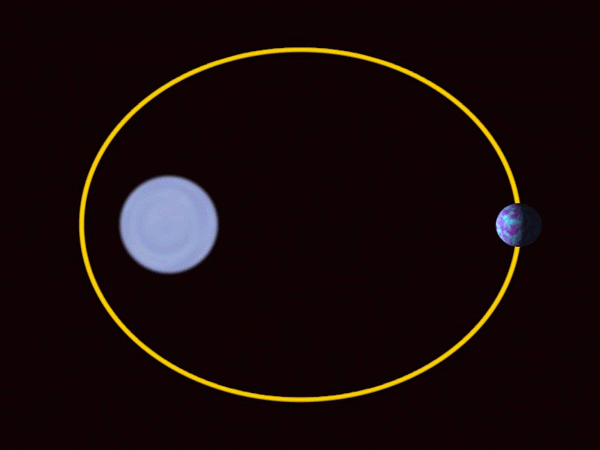Solsystemets planeter rör sig i elliptiska banor med solen i en av strålkastarna. Källa: Wikimedia Commons.

-Ellipsen används allmänt i arkitekturen som ett dekorativt och designelement.

-Genom att placera en reflektor i en av strålkastarna i en ellips reflekteras ljuset mot det andra fokuset. Detsamma händer med ljud. Det är därför som i ellipsformade hallar, som talar tyst att vara belägna i ett fokus hörs tydligt av lyssnare i det andra fokuset.

Det kan tjäna dig: hepagonalt prisma

-Samma egendom har en överraskande tillämpning inom medicinområdet. Njurberäkningar kan förstöras av ljud. Ultraljudvågor med stor intensitet genereras i en av fokuserna på ett elliptiskt badkar fullt av vatten, och patienten är belägen i det andra fokuset. Ljudvågor påverkar och reflekterar i beräkningen, och med sin energi fragmenterar de den i små bitar, som personen sedan lätt utvisar under urinering.

Hyperboli

-Vissa kometer i solsystemet följer hyperboliska banor, alltid med solen i en av focierna.

-Hyperbolas fokus är också mycket intressanta att studera fenomenen med vågreflektion. Till exempel, genom att rikta en strålstråle till fokus för en parabolisk spegel, återspeglas det i det andra fokuset, en mycket användbar egenskap för att bygga teleskop, eftersom ljuset kan fokusera på en parabolisk spegel och omdirigeras till en annan mer lämplig plats Enligt design.

-Kyltornen i kärnkraftverk har hyperbolas utformade silhuett.

-Innan GPS tillkomst användes hyperbolas i navigering för att hitta båtar. De fartyg som transporterades ombordssignaler som utfärdades samtidigt av Radio A- och B -stationerna och en dator var ansvarig för att registrera skillnaderna i ankomsttiderna för signalerna, för att förvandla dem till skillnader i avstånd från avstånd. På detta sätt är fartyget beläget i grenen till en hyperbola.

Proceduren upprepas med två andra radio C- och D -stationer, som placerar fartyget i grenen av En annan hyperbola. Båtens definitiva position är skärningspunkten mellan båda hyperbolorna.

Kan tjäna dig: Växande funktion: Hur man identifierar den, exempel, övningar

Omkrets

-Hjulets ankomst ändrade historiens gång.

-Den cirkulära rörelsen är mycket vanlig, många bitar kretsar för att ge olika effekter, från fabriker till fans.

-Även om banorna för de stora planeterna är elliptiska, är de cirkulära banorna bra tillvägagångssätt i många fall.

-Cirkunferenser är ofta element inom arkitektur, design, teknik och konstruktion. Listan över cirkulära eller skivformer är oändliga: mynt, cd, klockor och mer.

Exempel

Sedan finns det två koniker i planet, en cirkel och en ellips.

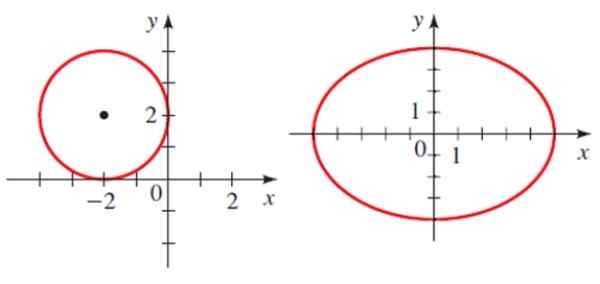Exempel på koniska avsnitt: en cirkel och en ellips. Källa: Stewart, J. Förkalkning.

Var och en har en analytisk ekvation:

Omkrets

(X-h)² + (Y-K)² = R²

Där h och k är koordinaterna för centrum och r är radion. För omkretsen som visas i figuren är ekvationen:

(x+2)² + (Y-2)² = 4

Ellips

Ellipsekvationen vars centrum är koordinatpunkten (h, k):

[(X-h)² /till² ]+ [(y-k)² /b² ] = 1

Där a och b är ellipsens halvpiler. För ellipsen som visas är centret vid punkt 0,0, den största semi -samma är densamma och den mindre semije är 4. Därför är dess ekvation:

(x² /25)+ (och² / 16) = 1

Referenser

1. Hoffman, J. Urval av matematikfrågor. Volym 2.
2. Jiménez, r. 2008. Algebra. Prentice hall.
3. Stewart, J. 2006. Preccculment: Matematik för beräkning. Femte. Utgåva. Cengage Learning.
4. Wikipedia. Koniskavdelning. Återhämtad från: är.Wikipedia.org.
5. Zill, D. 1984. Algebra och trigonometri. McGraw Hill.