Oktalsystem

Vad är ett oktalsystem?

han Oktalsystem Det är ett basnumreringssystem åtta (8); Det vill säga det består av åtta siffror, som är: 0, 1, 2, 3, 4, 5, 6 och 7. Därför kan varje siffra med ett oktalnummer ha valfritt värde från 0 till 7. Octal -nummer bildas av binära nummer.

Detta beror på att dess bas är en exakt kraft på två (2). Det vill säga de siffror som tillhör oktalsystemet bildas när de grupperas i tre på varandra följande siffror, beställda från höger till vänster, och därmed erhåller deras decimalvärde.

Octal Systems historia

Octal -systemet har sitt ursprung i forntida tider, när människor använde sina händer för att räkna åtta av åtta djur.

Till exempel, för att räkna antalet kor i en stall, började höger hand att ha tummen med lilla fingret; För att räkna det andra djuret, kom tummen samman med pekfingret, och så vidare med de återstående fingrarna på varje hand, tills den är klar 8.

Det finns möjligheten att det oktala numreringssystemet före decimalen för att kunna räkna de interdigitala utrymmena; det vill säga berätta för alla fingrarna förutom tummen.

Därefter upprättades det oktala numreringssystemet, som härstammar från det binära systemet, eftersom det behöver många siffror för att endast representera ett nummer; Därefter skapades Octal och Hexagonal Systems, som inte kräver så många siffror och som enkelt kan konvertera till det binära systemet.

Oktalnumreringssystem

Octal -systemet består av åtta siffror som sträcker sig från 0 till 7. Dessa har samma värde som i fallet med decimalsystemet, men deras relativa värde förändras beroende på den position som dessa ockuperar. Värdet på varje position ges av baskrafterna 8.

Det kan tjäna dig: regel t: egenskaper, så att det är exempel

Positionerna för siffrorna i ett oktalnummer har följande pesos:

8⁴, 8³, 8², 8¹, 8⁰, Octal Point, 8^-1, 8^-2, 8^-3, 8^-4, 8^-5.

Den stora oktalsiffriga är 7; På detta sätt ökar en siffra från 0 till 7 när det räknas i detta system från 0 till 7. När den når 7 återvinns den vid 0 för nästa räkning; Detta ökar följande siffriga position. Till exempel för att räkna sekvenser, i det oktalsystemet kommer det att vara:

• 0, 1, 2, 3, 4, 5, 6, 7, 10.
• 53, 54, 55, 56, 57, 60.
• 375, 376, 377, 400.

Det finns ett grundläggande teorem som tillämpas på det oktala systemet och uttrycks enligt följande:

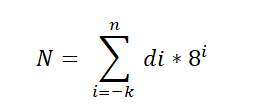
I detta uttryck representerar Di siffran multiplicerat med bas 8 -effekten, vilket indikerar positionsvärdet för varje siffra, på samma sätt på vilket det beställs i decimalsystemet.

Till exempel har du numret 543.2. För att ta det till oktalsystemet sönderdelas det på följande sätt:

N = ∑ [(5 _* 8²) + (4 _* 8¹) + (3 _*8⁰) + (2 _*8^-1)] = (5 * 64) + (4 * 8) + (2 * 1) + (2 * 0,125)

N = 320 +32 + 2 + 0,25 = 354 + 0,25_d

På så sätt har du 543.2_q = 354,25_d. Underskriften som indikerar att det är ett oktalnummer som också kan representeras av nummer 8; och abonnemang D hänvisar till decimalnumret, som också kan representeras med nummer 10.

Octal System -omvandling till decimal

För att konvertera ett oktalt systemnummer till dess motsvarande till decimalsystemet måste varje oktaltiffrigt multipliceras med sitt positionsvärde, från höger.

Exempel 1

732₈ = (7_* 8²) + (3_* 8¹) + (2_* 8⁰) = (7 _* 64) + (3 _* 8) + (2 _* 1)

732₈= 448 +24 +2

732₈= 474₁₀

Kan tjäna dig: matematisk jämlikhet

Exempel 2

26.9₈ = (2 _*8¹) + (6_* 8⁰) + (9_* 8^-1) = (2 _* 8) + (6 _* 1) + (9 _* 0,125)

26.9₈ = 16 + 6 + 1.125

26.9₈= 23,125₁₀

Decimalsystemomvandling till oktal

Ett decimal heltal kan omvandlas till ett oktalnummer med hjälp av den upprepade divisionsmetoden, där decimal heltal är uppdelat med 8 tills kvoten är lika med 0, och avfallet med varje division kommer att representera Octal -antalet.

Avfallet beställs från det sista till det första; det vill säga den första återstoden kommer att vara den minst betydande siffran för oktalnumret. På detta sätt kommer den mest betydelsefulla siffran att vara den sista återstoden.

Exempel

Octal of the Decimal nummer 266₁₀

- Decimalnummer 266 är uppdelat med 8 = 266/8 = 33 + 2 rest.

- Sedan är 33 uppdelat med 8 = 33/8 = 4 + 1 rest.

- 4 är uppdelat med 8 = 4/8 = 0 + 4 rest.

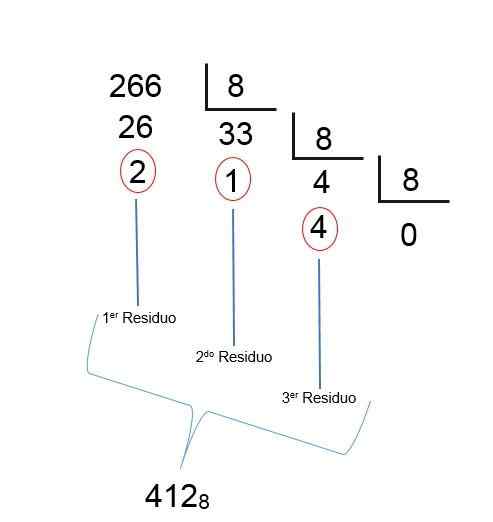
Som med den sista uppdelningen erhålls en kvot mindre än 1, det betyder att resultatet har hittats; Endast resterna måste beställas i omvänd riktning, så att det oktala antalet decimal 266 är 412, vilket kan ses i följande bild:

Binär oktalsystemomvandling

Omvandlingen av det oktala till binära systemet utförs vid konvertering av oktalsiffrorna till dess motsvarande binära siffra, bildad av tre siffror. Det finns en tabell som visar hur de åtta möjliga siffrorna blir:

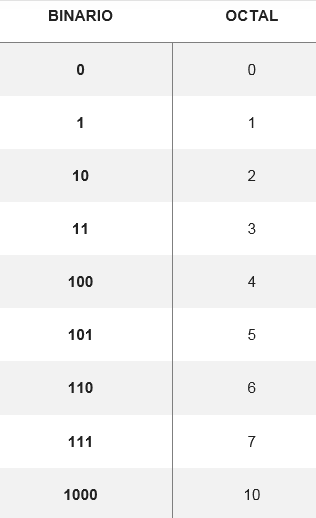
Från dessa omvandlingar kan du ändra valfritt antal Octal -system till binär, till exempel att konvertera nummer 572₈ Dina ekvivalenter söks i tabellen. Således måste du:

5₈ = 101

7₈= 111

2₈ = 10

Därför 572₈ motsvarande i det binära systemet till 10111110.

Binärt system till oktalomvandling

Processen för omvandling av integrerade siffror till oktal heltal är omvänd operation till föregående process.

Kan tjäna dig: Vilka är elementen i en vinkel?

Det vill säga de binära nummerbitarna grupperas i två grupper om tre bitar, från höger till vänster. Sedan görs binär till oktalomvandling med föregående tabell.

I vissa fall kommer det binära antalet inte att ha grupper om 3 bitar; För att slutföra det läggs en eller två nollor till vänster om den första gruppen.

För att ändra det binära nummer 11010110 till Octal görs till exempel:

- Grupper om 3 bitar bildas med början till höger (sista biten):

11010110

- Eftersom den första gruppen är ofullständig läggs en noll till vänster:

011010110

- Omvandlingen är gjord från tabellen:

011 = 3

010 = 2

110 = 6

På detta sätt motsvarar binärt nummer 011010110 326₈.

Omvandling av oktalsystemet till hexadecimal och vice versa

För att ändra ett oktalnummer till hexadecimal eller hexadecimal till oktalt system är det nödvändigt att antalet först kommer att vara binärt och sedan till önskat system.

För detta finns det en tabell där varje hexadecimal siffra representeras med dess likvärdighet i det binära systemet, bestående av fyra siffror.

I vissa fall kommer det binära antalet inte att ha grupper om 4 bitar; För att slutföra det läggs en eller två nollor till vänster om den första gruppen

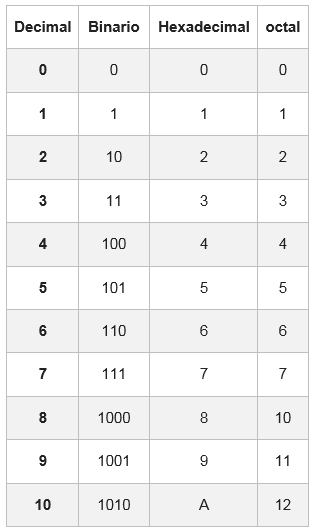
Exempel

Konvertera 1646 oktalnumret till ett hexadecimalt nummer:

- Octal till binär nummer blir

1₈ = 1

6₈ = 110

4₈ = 100

6₈ = 110

- Således 1646₈ = 1110100110.

- För att konvertera från binär till hexadecimal beställs de först i en grupp på 4 bitar, från höger till vänster:

11 1010 0110

- Den första gruppen är klar med nollor, så att den kan ha 4 bitar:

0011 1010 0110

- Hexadecimal binär systemomvandling görs. Ekvivalenserna ersätts med hjälp av tabellen:

0011 = 3

1010 = a

0110 = 6

På detta sätt motsvarar 1646 oktalnumret 3A6 i det hexadecimala systemet.