Summan av Riemanns historia, formler och egenskaper, övningar

De Riemanns summa Det är namnet som får den ungefärliga beräkningen av en definierad integral, med hjälp av en diskret summa med ett begränsat villkornummer. En vanlig applikation är tillvägagångssättet för funktioner i en grafik.

Det var den tyska matematikern Georg Friedrich Bernhard Riemann (1826-1866) som för första gången erbjöd en rigorös definition av integralen av en funktion i ett visst intervall. Han tillkännagav det i en artikel som publicerades 1854. 

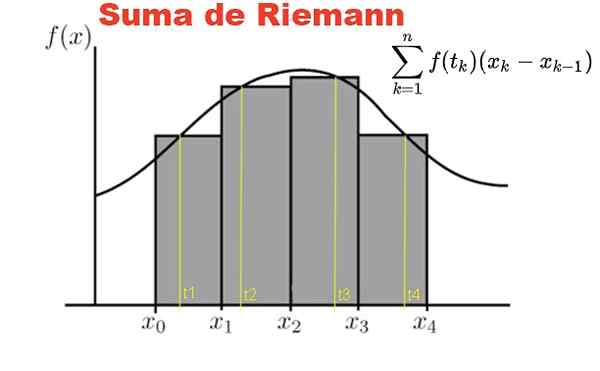
Figur 1. Riemanns summa definieras på en F -funktion och en partition i intervallet [x0, x1]. Källa: Fanny Zapata.

Riemanns summa definieras på en y = f (x) -funktion, med x som tillhör det stängda intervallet [a, b]. På detta intervall görs en partition P av N -element:

P = x₀= a, x₁, x₂,..., x_n= b

Detta innebär att intervallet är uppdelat enligt följande:

 Här t_k är mellan x_K-1 och x_k:

x_K-1 ≤ t_k ≤ x_k

Figur 1 visar summan av Riemann för F -funktionen i intervallet [x₀, x₄] På en partition av fyra underintervaler, grå rektanglar.

Summan representerar rektanglarnas totala yta och resultatet av denna summa är numeriskt tillvägagångssätt till området under kurvan f, bland abscissas x = x₀ y x = x₄.

Naturligtvis förbättras tillvägagångssättet till området under kurvan kraftigt i den utsträckning antalet n av partitioner är större.  På detta sätt konvergerar summan till området under kurvan, när antalet n Partitioner tenderar att oändliga.

[TOC]

Formler och egenskaper

Riemanns summa av f (x) -funktion vid partition:

Kan tjäna dig: Rhomboid: Egenskaper, hur man tar ut omkretsen och området

P = x₀= a, x₁, x₂,..., x_n= b

Definieras på intervallet [a, b], det ges av:

S (p, f) = ∑_{K = 1}ⁿ med_k) (x_k - x_K-1) 

Där t_k Det är ett värde i intervallet [x_k, x_K-1]. I summan av Riemann används regelbundna breddsintervaller vanligtvis Δx = (b - a)/n, där a och b är minsta och maximala värden för abscissen, medan n är antalet underavdelningar.

I så fall Riemanns högra summa är:

SD (f, n) = [f (a+Δx)+f (a+2Δx)+...+f (a+(n-1) Δx)+f (b)]*Δx

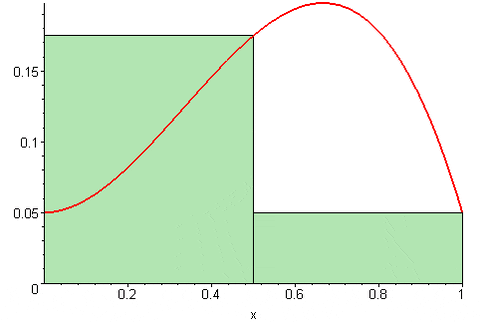figur 2. Riemanns högra summa. Källa: Wikimedia Commons. 09Glasgow09 [CC BY-SA (https: // Creativecommons.Org/licenser/BY-SA/3.0)].

Medan Riemanns vänstra summa Det uttrycks som:

Ja (f, n) = [f (a)+f (a+Δx)+...+f (a+(n-1) Δx)]*Δx

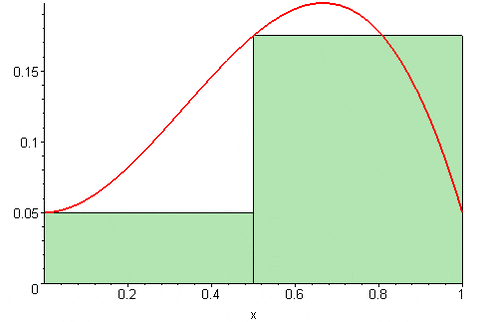Figur 3. Summan av Riemann kvar. Källa: Wikimedia Commons. 09Glasgow09 [CC BY-SA (https: // Creativecommons.Org/licenser/BY-SA/3.0)]

Äntligen Riemann Central Sum är:

Sc (f, n) = [f (a+Δx/2)+f (a+3Δx/2)+...+f (b- Δx/2)]*Δx

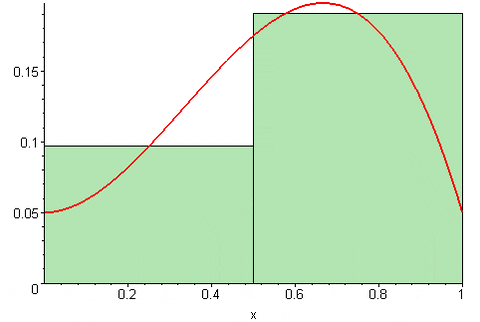Figur 4. Mellanliggande summa av Riemann. Källa: Wikimedia Commons. 09Glasgow09 [CC BY-SA (https: // Creativecommons.Org/licenser/BY-SA/3.0)]

Beroende på var punkt T finns_k I intervallet [x_k, x_K-1] Riemanns summa kan överskatta eller underskatta det exakta värdet på området under y = f (x) -funktionskurvan (x). Det vill säga rektanglarna kan utmärka sig från kurvan eller vara lite under detta.

Området under kurvan

Den huvudsakliga egenskapen för summan av Riemann och som dess betydelse blir, är att om antalet underavdelningar tenderar att oändliga, är resultatet av summan konvergerar till den definierade integralen av funktionen:

Det föregående uttrycket motsvarar definitionen av Riemanns integral och tillämpar förutsatt att F -funktionen är kontinuerlig och mjuk. För mer speciella funktioner finns det andra definitioner av de integrerade (integrerade de stieldjes och integrerade de Lebesgue).

Det kan tjäna dig: Standard Uppskattningsfel: Hur det beräknas, exempel, övningar

Löst övningar

- Övning 1

Beräkna värdet på den integrerade definierade mellan A = -2 till B = +2 i funktionen:

f (x) = x²

Använd en summa av Riemann. För att göra detta, hitta summan för regelbundna partitioner av intervallet [a, b] och ta sedan den matematiska gränsen för det fall som antalet partitioner lagrar till oändligheten. 

Lösning

Det här är stegen att följa:

-Först definieras partitionsintervallet som: 

Δx = (b - a)/n. 

-Då är summan av Riemann till höger motsvarande funktionen f (x) så här:

-Nu ersätts de a = -2 och b =+2, så att intervallet eller steget Δx = 4/n. Det vill säga att summan av Riemann för funktionen f (x) = x² är:

-Sedan utvecklas fyrkantiga binomial: 

[-2 +(4i/n)]² = 4 - (16 I /N) + (4 /n)² Yo²

-Och sedan ersätts den noggrant i summan:

-Nästa steg är att separera sammanfattningarna och ta bort de ständiga mängderna som en vanlig faktor för varje summa. Det är nödvändigt att ta hänsyn till att indexet är i, därför siffrorna och villkoren med n De betraktas som konstant:

-Varje summa utvärderas, eftersom det för var och en av dem finns lämpliga uttryck. Till exempel den första av sammanfattarna da n:

Den andra är:

 Och den tredje är:

 -Genom att ersätta resultaten från sammanfattningar i summan av Riemann erhålls det äntligen:

S (f, n) = 16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6N²

-Slutligen måste du beräkna integralen är:

= lim_N➝∞ [16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²] =

= 16 -(64/2) + (64/3) = 16/3 = 5.333

Läsaren kan verifiera att detta är det exakta resultatet, som kan erhållas genom att lösa den obestämda integralen och utvärdera gränserna för integration av Barrow -regeln.

Kan tjäna dig: hur man konverterar från km/h a m/s? Löst övningar

- Övning 2

Bestäm ungefär området under funktionen: 

f (x) = (1/√ (2π) e^(-x2/2)

Mellan x = -1 och x =+1 med en central summa av Riemann med 10 partitioner. Jämför med det exakta resultatet och uppskatta den procentuella skillnaden.

Lösning

Steget eller ökningen mellan två på varandra följande diskreta värden är:

Δx = (1 - (-1)/10 = 0,2

Så att P -partitionen på vilken rektanglarna definieras är så här:

P = -1,0; -0,8; -0,6; -0.4; -0,2; 0,0; 0,2; 0,4; 0,6; 0,8; 1.0

Men som vad du vill är den centrala summan, kommer funktionen f (x) att utvärderas i mitten av underintervalen, det vill säga i uppsättningen:

T = -0,9; -0,7; -0,5; -0,3; -0,1; 0,1; 0,3; 0,5; 0,7; 0,9.

Riemanns summa (centrala) är så här:

S = F (-0,9)*0,2 +F (-0,7)*0,2 +F (-0,5)*0,2 +... +F (0,7)*0,2 +F (0,9)*0,2

Eftersom F -funktionen är symmetrisk är det möjligt att minska summan till endast 5 termer och resultatet multipliceras med två:

S = 2*0,2*F (0,1)+ F (0,3)+ F (0,5)+ F (0,7)+ F (0,9)

S = 2*0,2*0,397+ 0,381+ 0,352+ 0,312+ 0,266 = 0,683

Funktionen i detta exempel är ingen annan än den välkända Gauss -klockan (normaliserad, med genomsnitt lika med noll och standardavvikelse en). Det är känt att området under kurvan i intervallet [-1,1] för denna funktion är 0,6827.

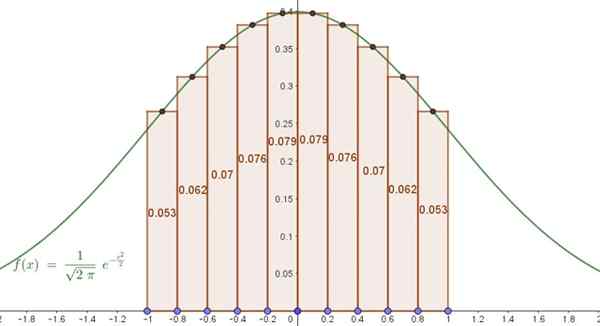Figur 5. Område under en ungefärlig Gauss -klocka med en summa av Riemann. Källa: f. Zapata.

Detta innebär att den ungefärliga lösningen med bara 10 termer sammanfaller med den exakta lösningen upp till tre decimaler. Det procentuella felet mellan den ungefärliga integralen och det exakta är 0,07%.

Referenser

1. Casteleiro, J. M., & Gómez-Alvarez, R. P. (2002). Omfattande beräkning (illustrerad ED.). Madrid: ESIC -redaktion.
2. Oanisk. Historia om begreppet integrerad. Återhämtat sig från: arkiv.Oanisk.är
3. Uis. Riemann summor. Återhämtat sig från: matematik.Uis.Edu.co
4. Wikipedia. Riemanns summa. Återhämtad från: är.Wikipedia.com
5. Wikipedia. Integration av Riemann. Återhämtad från: är.Wikipedia.com