Sats om existens och unikhetsdemonstration, exempel och övningar

han Existens och unikhetsteorem fastställer de nödvändiga och tillräckliga villkoren för en första -ordningens differentiella ekvation, med ett givet initialt villkor, att ha en lösning och att denna lösning också är den enda. 

Satsen ger emellertid ingen teknik eller indikation på hur man hittar en sådan lösning. Förekomsten och unikhetsteoremet sträcker sig också till differentiella ekvationer med högre ordning med initiala förhållanden, vilket kallas Cauchy -problem.

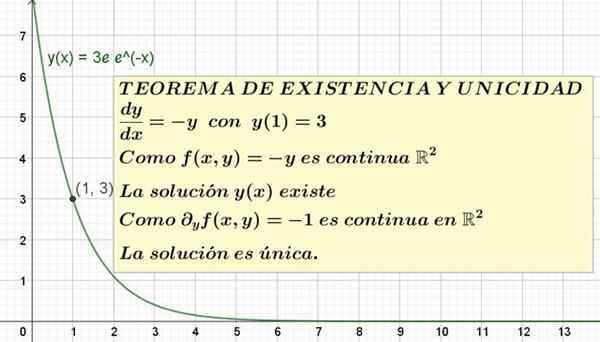
Figur 1. En differentiell ekvation med initialt tillstånd och dess lösning visas. Förekomsten och unikhetsteoremet garanterar att det är den enda möjliga lösningen.

Det formella uttalandet om existensen och det unika teoremet är som följer:

"För en differentiell ekvation och '(x) = f (x, y) med initialt skick och (a) = b,  existerar Minst en lösning i en rektangulär region i planet Xy som innehåller punkten (A, B), Ja f (x, y) Det är kontinuerligt i den regionen. Och om det partiella derivatet av F med respekt för och: G = ∂f/ ∂y Det är kontinuerligt i samma rektangulära region, så lösningen är unik i en miljö i punkten (A, B) innehåll i kontinuitetsregionen i F och g."

Användbarheten av detta sats ligger först att veta vad som är regionerna i XY -planet där det kan finnas en lösning och också veta om den hittade lösningen är den enda möjliga eller om det finns andra. 

Observera att i händelse av att villkoret för unikt.

[TOC]

Demonstration av existensen och unikhetssatsen

figur 2. Till Charles Émile Picard (1856-1941) En av de första demonstrationerna av existensen och unikhetsteoremet är ackrediterat. Källa: Wikimedia Commons.

För detta teorem är två möjliga demonstrationer kända, en av dem är demonstrationen av Charles émile Picard (1856-1941) och den andra beror på Giuseppe Peano (1858-1932) baserat på verk av Augustin Louis Cauchy (1789-1857 ).

Kan tjäna dig: samtidiga vektorer: egenskaper, exempel och övningar

Det bör noteras att de ljusaste matematiska sinnen från 1800 -talet deltog i demonstrationen av detta teorem, så det kan vara intuit att ingen av dem är enkla.

För att formellt visa teoremet är det nödvändigt att först etablera en serie mer avancerade matematikbegrepp, såsom Lipschitz -typfunktioner, Banach -utrymmen, caratheodory och flera existenssteorem, som undviker artikeln.

En stor del av de differentiella ekvationerna som hanteras i fysiken handlar om kontinuerliga funktioner i regionerna av intresse, därför kommer vi att begränsa oss till att visa hur teoremet tillämpas i enkla ekvationer.

Exempel

- Exempel 1

Tänk på följande differentiella ekvation med ett initialt tillstånd:

och '(x) = - y; med och (1) = 3

Finns det en lösning för detta problem? Är det den enda möjliga lösningen?

Svar

För det första utvärderas förekomsten av lösningen av differentiell ekvation och att den också uppfyller det initiala tillståndet. 

I det här exemplet f (x, y) = - y Tillståndet i existensen kräver att veta om  f (x, y) Det är kontinuerligt i ett planregion Xy som innehåller koordinatpunkten x = 1, y = 3.

Men f (x, y) = -y Det är besläktad funktion, vilket är kontinuerligt inom området för verkliga siffror och finns i hela verkliga siffror.

Därför dras slutsatsen att f (x, y) är kontinuerlig i r², Så satsen garanterar förekomsten av åtminstone en lösning.

Att veta detta är det dags att bedöma om lösningen är unik eller om det tvärtom finns mer än en. För detta är det nödvändigt att beräkna det partiella derivatet av F När det gäller variabeln och:

∂f/∂y = ∂ (-y)/∂y = -1

Så G (x, y) = -1 vilket är en konstant funktion, som också definieras för alla r² Och det är också kontinuerligt där. Av detta följer att existensen och unikhetsteoremet garanterar att detta initialvärdeproblem har en unik lösning, även om den inte berättar vad det är.

Kan tjäna dig: konvex polygon: definition, element, egenskaper, exempel

- Exempel 2

Tänk på följande första ordinarie differentiell ekvation med initialt tillstånd:

och '(x) = 2√y; och (0) = 0.

Finns det en lösning och (x) För detta problem? Om så är fallet, bestäm om det finns en eller flera än en.

Svar

Vi överväger funktionen f (x, y) = 2√y. Funktionen F definieras endast för y≥0, Vi vet att ett negativt antal saknar verklig rot. Förutom f (x, y) Det är kontinuerligt i den övre semiplanen av R²  inklusive X -axeln, så Garantiets existens och unika teorem Minst en lösning i den regionen.

Nu är det initiala tillståndet x = 0, y = 0 i utkanten av lösningsregionen. Sedan tar vi det partiella derivatet av f (x, y) med avseende på y:

∂f/∂y = 1/√y

I detta fall är funktionen inte definierad för y = 0, precis där det initiala villkoret är.

Vad säger till oss teoremet? Den säger till oss att även om vi vet att det finns åtminstone en lösning den övre semiplanen i x -axeln inklusive X -axeln, eftersom tillståndet för unikhet inte uppfylls, finns det ingen garanti för att det finns en enda lösning.

Detta innebär att det kan finnas en eller flera av en lösning i kontinuitetsregionen i F (x, y). Och som alltid berättar teoremet inte vad som kan vara.

Löst övningar

- Övning 1

Lös Cauchy -problemet i exempel 1:

och '(x) = - y; med och (1) = 3. 

Hitta funktionen y (x) som uppfyller differentiell ekvation och det initiala tillståndet.

Lösning

I exempel 1 fastställdes att detta problem har en lösning och också är unik. För att hitta lösningen är det första som bör noteras att det är en första gradisk differentiell ekvation av separerbara variabler, som är skriven enligt följande:

Kan tjäna dig: Variationskoefficient: Vad är det för, beräkning, exempel, övningar

dy /dx = - och → dy = -y dx

Dela mellan och i båda medlemmarna för att separera de variabler vi har:

dy/y = - dx

Obestämd integral i båda medlemmarna tillämpas:

∫ (1/y) dy = - ∫dx

Att lösa de obestämda integralerna är:

ln (y) = -x + c

där C är en konstant för integration som bestäms av det initiala villkoret:

ln (3) = -1 + c, det vill säga att c = 1 + ln (3)

Att ersätta värdet på C och omorganisera är:

ln (y) - ln (3) = -x + 1

Tillämpa följande egenskap hos logaritmerna:

Skillnaden i logaritmer är kvotlogaritmen

Det föregående uttrycket kan skrivas om så här:

ln (y/3) = 1 - x

Exponentiell funktion tillämpas med båda medlemmarna för att få:

Y / 3 = e^{(1 - x)}

Vilket motsvarar:

 y = 3e e^-x

Detta är den unika lösningen av ekvationen och '= -y med y (1) = 3. Grafen för denna lösning visas i figur 1.

- Övning 2

Hitta två lösningar på det problem som tas upp i exempel 2:

och '(x) = 2√ (y); och (0) = 0.

Lösning

Det är också en ekvation av separata variabler, som skrivs differentiellt återstår:

Dy / √ (y) = 2 dx

Att ta den obestämda integralen i båda medlemmarna kvarstår:

2 √ (y) = 2 x + c

Som är känt det y≥0 I lösningsområdet har vi:

y = (x + c)² 

Men eftersom det initiala villkoret x = 0, y = 0 måste uppfyllas, är konstanten c noll och följande lösning kvarstår:

och (x) = x².

Men denna lösning är inte unik, funktionen y (x) = 0 är också en lösning av problemet som tas upp. Existensen och unikhetsteoremet som tillämpades på detta problem i exempel 2 hade redan förutspått att det kunde finnas mer än en lösning.

Referenser

1. Coddington, Earl a.; Levinson, Norman (1955), Theory of Ordinary Differential Equations, New York: McGraw-Hill.
2. Encyklopedi av matematik. Cauchy-Lipschitz teorem. Återhämtad från: encyklopediaofmath.org
3. Lindelöf, South l'A -tillämpning av metoden des Approximations Auccesce aux équations différentielles Ordinaires du Premier Ordre; Compttes RenDus Hebdomadaires des Séances de l'Cn Acadequie des Sciences. Vul. 116, 1894, sid. 454-457. Återhämtat sig från: gallic.Bnf.fr.
4. Wikipedia. Picards metod för successiva tillvägagångssätt. Återhämtad från: är.Wikipedia.com
5. Wikipedia. Picard-Lindelö-teorem. Återhämtad från: är.Wikipedia.com.
6. Zill, D.1986. Elementära differentiella ekvationer med applikationer.Prentice hall.