Grön teorem, demonstration, applikationer och övningar

han Grönt sats Det är en beräkningsmetod som används för att relatera linjeintegraler med dubbla områden eller ytintegraler. De involverade funktionerna måste betecknas som vektor och definierade fält inom bana C.

Till exempel kan ett uttryck för integrerad linje vara mycket komplicerat att lösa; Men vid implementering av Green's Theorem blir dubbla integraler ganska grundläggande. Det är alltid viktigt att respektera den positiva känslan av banan, detta hänvisar till klockornas riktning.

Green's Theorem är ett särskilt fall av Stokes sats, där projektionen av vektorfunktionen utförs i XY -planet.

[TOC]

Definition

Gröns uttryck för Green's sats är som följer:

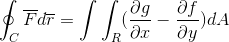
Under den första terminen observeras linjen integrerad definierad av banan "C", av produktskalär mellan vektorfunktionen "F" och den för vektorn "R".

C: Det är den definierade banan som vektorfunktionen kommer att projiceras så länge den definieras för det planet.

F: Vektorfunktion, där var och en av dess komponenter definieras av en funktion som sådan (F, G).

S: Det är en vektortangent till R -regionen som integralen definieras. I det här fallet drivs det med en skillnad av denna vektor.

Under den andra terminen ser vi Green utvecklad sats, där den dubbla integrerade definierade i regionen R av skillnaden mellan partiella derivat av G och F observeras, med avseende på X respektive och respektive. För en områdesdifferential som inte är mer än produkten från båda två dimensionella differentialer (DX.dy).

Detta sats är perfekt tillämpligt för rymd- och ytintegraler.

Demonstration

För att demonstrera Green's sats på ett enkelt sätt kommer denna uppgift att delas upp i två delar. Först antar vi att vektorn F -funktionen bara har en definition i Versor Yo. Medan "G" -funktionen motsvarar Versor J kommer att vara lika med noll.

Kan tjäna dig: hur många hundratals passar in i en tiondel? (Exempel)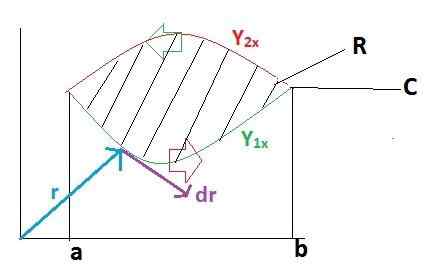Författare

F = f (x, y)Yo + G (x, y)J = f (x, y)Yo + 0

R = xYo + ochJ

Dr = dxYo + DyJ

Först utvecklar vi linjen integrerad över banan C, för vilken banan har sektoriserats i två sektioner som går först från A till B och efter B till en.

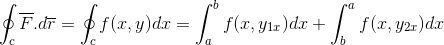
Definitionen av den grundläggande teoremet för beräkningen för en definierad integral tillämpas.

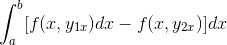
Uttrycket omarrangeras i en enda integral, görs gemensamt för det negativa och ordningen på faktorerna vänds.

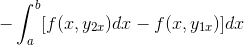
Genom att observera i detalj detta uttryck blir det uppenbart att vid tillämpning av kriterierna för primitiv funktion är det i närvaro av integralen av uttrycket härrörande från F med avseende på och. Utvärderas i parametrar

[och_1x , och_2x]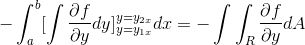

Nu räcker det att anta att Vector Fun -funktionen endast definieras för G (X, Y)J. Där när det fungerar på ett sätt som är homologat till föregående fall, erhålls det:

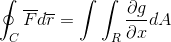
Slutligen tas de två demonstrationerna. På detta sätt visas det som linjen integrerad efter att ha definierat och betraktats som en en -dimensionell bana, den kan utvecklas fullt ut för planet och rymden.

F = f (x, y)Yo + G (x, y)J

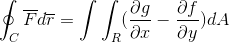
På detta sätt demonstreras Green's teorem.

Ansökningar

Gröna teoremapplikationer är breda i grenarna i fysik och matematik. Dessa sträcker sig till alla applikationer eller användningar som kan ges till linjeintegration.

Det mekaniska arbetet som utförs av en kraft F genom en bana C, kan utvecklas av en linjeintegral som uttrycks som en dubbel integral av ett område genom Green's Theorem.

Kan tjäna dig: Pentagonal Prism: Egenskaper, delar, vertikaler, kanter, volym

Momenten av tröghet hos många kroppar som utsätts för yttre krafter vid olika tillämpningspunkter svarar också på utvecklingsbara integraler med Green's teorem.

Detta har flera funktioner i resistensstudier av material som används. Där externa värden kan kvantifieras och beaktas före utarbetandet av olika element.

I allmänhet underlättar Green's Theorem förståelsen och definitionen av områden där vektorfunktioner definieras med avseende på en region enligt en bana.

Historia

Det publicerades 1828 i arbetet Matematisk analys till teorier om el och magnetism, Skrivet av den brittiska matematikern George Green. Den undersöker ganska avgörande sektioner i tillämpningen av beräkning i fysik, till exempel begreppet potential, funktioner för grönt och tillämpningarna av dess autosats med titeln.

George Green formaliserade sin studentkarriär vid 40 års ålder, hittills en helt självutbildad matematiker. Efter att ha studerat vid University of Cambridge fortsätter hans forskning och ger bidrag inom området akustik, optik och hydrodynamik som fortfarande är i kraft idag.

Relation med andra teorier

Green's Theorem är ett speciellt fall och uppstår från 2 andra mycket viktiga teorier i beräkningsgrenen. Dessa är Kelvin-Stokes 'sats och divergens eller Gausski-teorem.

Från något av båda satserna kan du nå Green's teorem. Vissa definitioner och förslag är nödvändiga för att utveckla dessa demonstrationer.

Övningar

- Följande övning visar hur man förvandlar en linjeintegral till en dubbel integral med avseende på en region r.

Det ursprungliga uttrycket är som följer:

Kan tjäna dig: hur mycket är x värt?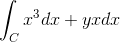

Och måste utvärderas i den triangulära regionen som ansluter sig till punkterna (0, 0), (1, 0), (0, 1) betecknas med C. För det här fallet kommer den positiva känslan av svängen att övervägas.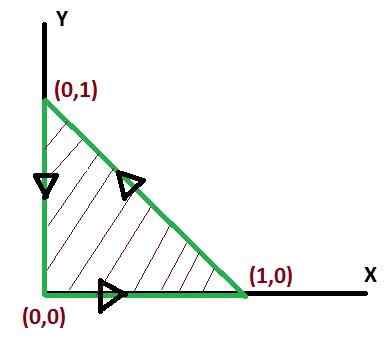

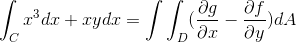
Där funktionerna som motsvarar F och G är hämtade från

f (x, y) = x³                      g (x, y) = yx

df/dy = 0 dg/dx = y

Det är viktigt att definiera de funktioner som utgör gränserna för regionen C, att kunna montera den differentiella produkten som helt täcker regionen.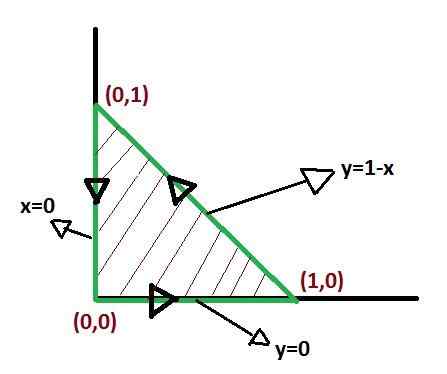

Det finns inget unikt sätt att definiera integrationsgränser när man tillämpar Green's Theorem. Men det finns former där integraler efter att ha definierats kan vara enklare. På ett sådant sätt att optimering av integrationsgränser förtjänar uppmärksamhet.

För detta fall övervägs detta uttryck: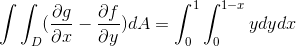

Var i att lösa integralerna får vi:

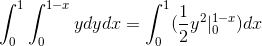
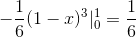
Detta värde motsvarar kubiska enheter till regionen under vektorfunktionen och på den triangulära regionen definierad av C.

När det gäller linjen integrerad utan att utföra den gröna metoden skulle det ha varit nödvändigt att parametrera funktionerna i varje avsnitt i regionen. Det vill säga, gör 3 parametrerade integraler för upplösning. Detta är tillräckligt bevis på effektiviteten som Robert Green bidrog med hans teorem till beräkningen.

Referenser

1. Introduktion till kontinummekanik. W Michael Lai, David H. Rubin, Erhard Krempl, David Rubin Butterworth-Heinemann, 23 juli. 2009
2. Multivariabel kalkyl. James Stewart. Cengage Learning, 22 mar. 2011
3. En informell historia av Green's teorem och tillhörande idéer. James Joseph Cross. Institutionen för matematik, University of Melbourne, 1975
4. Värmebeteende med greenfunktioner. Kevin d. Cole, James V. Beck, a. Haji-Sheikh, Bahman Luckouhi. Taylor & Francis, 16 juli. 2010
5. Tillämpning av Green's teorem på extremiseringen av linjära integraler. Defense Technical Information Center, 1961