Steiner förklaringsteorem, applikationer, övningar

han Steiners teorem, också känd som Parallell axelsats, Det gör det möjligt att utvärdera tröghetsmomentet i en utökad kropp, runt en axel som är parallell med en annan som passerar genom objektets centrum.

Det upptäcktes av den schweiziska matematiska_Centimeter objektets tröghetsmoment med avseende på en axel som passerar genom dess CM och I Mass Center_z tröghetsmomentet med avseende på en annan parallell axel till detta.

Figur 1. En rektangulär dörr som vänder på sina glädje har ett ögonblick av tröghet som kan beräknas genom att tillämpa Steiners teorem. Källa: Pixabay.

Känt avståndet d som skiljer både axlar och massan m från den aktuella kroppen, tröghetsmomentet med avseende på inkognito -axeln är:

Yo_z = Jag_Centimeter + VD²

Tröghetsmomentet indikerar hur lätt det är för ett objekt att rotera runt en viss axel. Det beror inte bara på kroppens kropp, utan på hur den distribueras. Av denna anledning är det också känt som Rotationsinerti, Att vara dina enheter i det internationella KG -systemet . m².

Satsen visar att tröghetsmomentet Yo_z Det är alltid större än tröghetsmomentet Yo_Centimeter i ett belopp som ges av M.D².

[TOC]

Ansökningar

Eftersom ett föremål kan rotera runt många axlar, och i tabellerna vanligtvis bara tröghetsmomentet när det gäller axeln som passerar genom centroiden, underlättar Steiners teorem beräkningen när den behöver rotera kroppar på axlar på axlar som inte sammanfaller med sammanfaller med detta.

Kan tjäna dig: rätlinjig rörelse: egenskaper, typer och exempel

Till exempel kretsar en dörr vanligtvis inte kring en axel som passerar genom dess masscentrum, utan med avseende på en sidodel, där gångjärnen följer.

När man känner till tröghetsmomentet är det möjligt att beräkna den kinetiska energin associerad med rotationen på denna axel. Ja K är kinetisk energi, Yo tröghetsmomentet runt axeln i fråga och Ω Vinkelhastigheten uppfylls att:

K = ½ i.Ω²

Denna ekvation är mycket lik den mycket bekanta formeln för kinetisk energi för ett massobjekt M rör sig i hastighet v:  K = ½ m.v². Och är det ögonblicket av tröghet eller roterande tröghet Yo spelar i rotation samma roll som degen M I översättningen.

Demonstration av Steiners teorem

Tröghetsmomentet för ett utökat objekt definieras som:

I = ∫r² Dm

Var Dm Det är en oändlig massa massa av massor och r Det är avståndet mellan Dm och rotationsaxeln z. I figur 2 korsar denna axel mitten av massan CM, men den kan vara vem som helst.

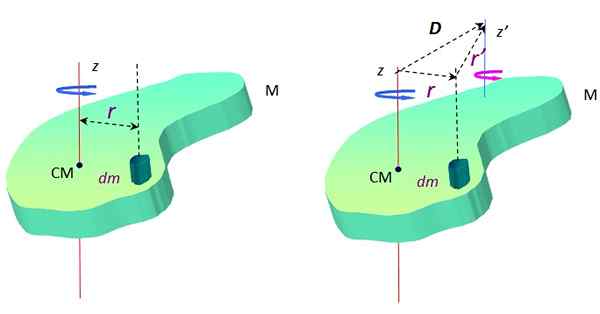figur 2. Ett objekt som sträcker sig i rotation runt två parallella axlar. Källa: f. Zapata.

Runt en annan axel  z ', Tröghetsmomentet är:

Yo_z= ∫ (R ')² Dm

Nu, enligt triangeln som bildas av vektorerna D, r och R ' (Se figur 2 till höger), det finns en vektor summa:

r + R ' = D   → R ' = D - r

De tre vektorerna är på objektets plan som kan vara Xy. Ursprunget till koordinatsystemet (0,0) väljs i CM för att underlätta beräkningarna som följer.

På detta sätt är vektorns fyrkantiga modul R ' är:

Kan tjäna dig: Biofysik: Historia, vilka studier, applikationer, koncept, metoder

(R ')² = (D_x- r_x)² +(D_och - r_och)² =

= D_x² + D_och² +r_x² + r_och2 -2d_xr_x - 2 d_ochr_och =

= D² + r²  - 2d_xr_x - 2 d_ochr_och

Nu ersätts denna utveckling i integralen av tröghetsmomentet i_z och även definitionen av densitet DM = ρ används.DV:

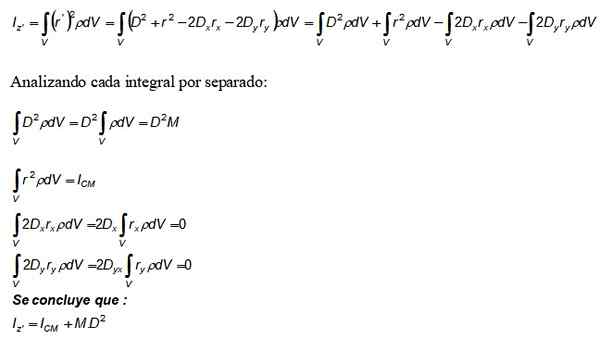
Termen m. D² som visas i Steiners sats kommer från den första integralen, den andra är tröghetsmomentet när det gäller axeln som passerar genom CM.

För sin del är de tredje och fjärde integralerna värda 0, eftersom de per definition utgör positionen för CM, som har valts som ursprunget till koordinatsystemet (0,0).

Löst övningar

-Motion Löst 1

Den rektangulära dörren i figur 1 har en massa på 23 kg, 1,30 bred och 2,10 m hög. Bestäm tröghetsmomentet för dörren angående axeln som passerar genom glädjen, förutsatt att dörren är tunn och enhetlig.

Figur 3. Schema för exemplet löst 1. Källa: Modifierad Pixabay.

Lösning

Från ett bord med tröghetsmoment, för en rektangulär platta med massa M och dimensioner till och b, Tröghetsmomentet med avseende på axeln som passerar genom dess masscentrum är: i_Centimeter = (1/12)M(till² + b²).

En homogen dörr antas (en metod, eftersom dörren till figuren förmodligen inte är så mycket). I detta fall passerar masscentrumet genom dess geometriska centrum. I figur 3 har en axel som passerar genom masscentret ritats och som också är parallell med axeln som passerar genom glädjen.

Yo_Centimeter = (1/12) x 23 kg x (1.30²+2.10²) m² = 11.7 kg.m²

Kan tjäna dig: vad är en geoid?

Tillämpa Steiners teorem för den gröna rotationsaxeln:

I = i_Centimeter + VD² = 11.7 kg.m² + 23 kg x 0.652 m² = 21.4 kg.

-Motion Löst 2

Hitta tröghetsmomentet för en tunn homogen stav när den kretsar med avseende på en axel som passerar genom en av dess ändar, se figur. Är det större eller mindre än tröghetsmomentet när det kretsar kring dess centrum? Därför att?

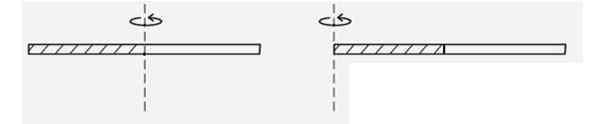Figur 4. Schema för exemplet löst 2. Källa: f. Zapata.

Lösning

Enligt tröghetsmomenten är tröghetsmomentet Yo_Centimeter av en tunn degstång M och längd L är: Yo_Centimeter = (1/12) ml²

Och Steiners sats säger att när den roteras runt en axel som passerar genom ena änden D = l/2 kvarstår:

I = i_Centimeter + VD² = (1/12) ml² + M (l/2)² = (1/3) ml²

Den är gammal.

Avståndets påverkan till rotationsaxeln är inte linjär, men kvadratisk. En massa som är dubbelt så mycket som en annan kommer att ha ett ögonblick av tröghet proportionell mot (2d)² = 4d².

Referenser

1. Bauer, w. 2011. Fysik för teknik och vetenskap. Volym 1. MC Graw Hill. 313-340.
2. Georgia State University. Rotationsrörelse. Återhämtat sig från: phys.Nthu.Edu.Tw.
3. Parallell axelsats. Återhämtat sig från: hyperfysik.Phy-astrage.Gsu.Edu.
4. Rex, a. 2011. Fysikens grunder. Pearson. 190-200.
5. Wikipedia. Parallell axelsats. Hämtad från: i.Wikipedia.org