Miletus sådan teorem

Vi förklarar den första och den andra satsen för sådant, med exempel och övningar löst

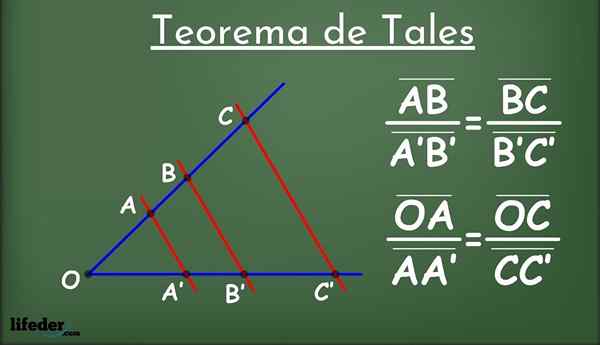
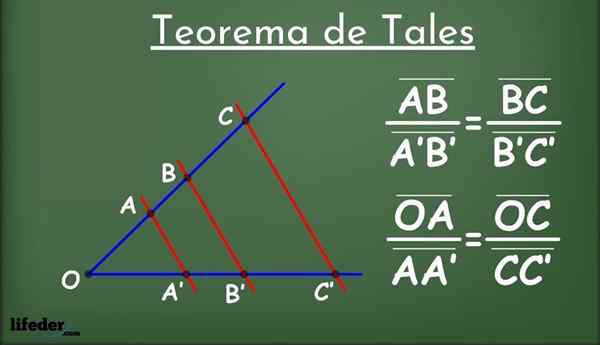Figur 1.- Tales Theorem

Vad är sådant?

han en sådan teorem Från Miletus hänvisar han faktiskt till flera geometri -teorier som tillskrivs den kloka av forntida Greklands thales av Miletus, som bodde från 624 till 546 AC i Miletus, nuvarande Turkiet.

Förutom matematiker och geometer var det en filosof som erkändes för hans stora skärpa. Det sägs att han lyckades mäta höjden på den stora pyramiden genom användning av ett av dess teorem.

han Första satsen för sådant Det hänvisar till de segment som en grupp av parallella linjer bestämmer i två linjer i planet. Dessa segment håller ett förhållande mellan proportionalitet, som kommer att ses inom kort, som utvidgas till sidorna av två trianglar, förutsatt att vissa villkor är uppfyllda.

Detta sats är oerhört användbart i praktiken, eftersom det gör det möjligt att bestämma höjden på mycket hög eller svår att komma åt strukturer, utan att behöva mäta dem direkt. Det var just vad berättelser gjorde när han mätte höjden på den stora pyramiden.

För sin sida Andra satsen för detta Länkpunkter som tillhör en omkrets med en rektangel triangel registrerad i den, vars hypotenus sammanfaller med dess diameter.

Första satsen för sådant

Vara två rader i ett plan, kallad L₁ och jag₂ (i blått i figur 1) och en grupp linjer parallella med varandra (i rött) som korsar L₁ och jag₂.

De parallella linjerna delar upp linjerna i segment l₁ och jag₂: Ab, a'b ', bc, b'c' och så vidare. Bland de segment som står inför är följande proportionalitetsförhållande etablerat:

I denna figur beräknas till exempel måttet på "X" -segmentet av teoremet för sådant, eftersom linjerna korsas av flera paralleller som bestämmer segment med känd längd:

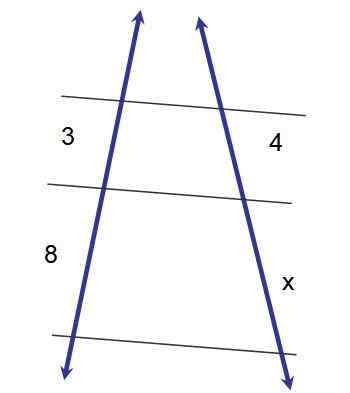Det kan tjäna dig: ömsesidigt exklusiva evenemang: egenskaper och exempelfigur 2.- Tillämpning av den första sådana teoremet för att bestämma måtten på segment X. Källa: f. Zapata.

3x = 32

x = 32/3 ≈ 10.7

Det sådana teoremet för liknande trianglar

Satsen kan utvidgas till trianglarna enligt följande: Anta att det finns en ABC -triangel på vilken ett parallellt segment dras till en av dess sidor. På detta sätt erhålls två liknande trianglar: ABC och DEC, vars inre vinklar är kongruenta, det vill säga de har lika mått.

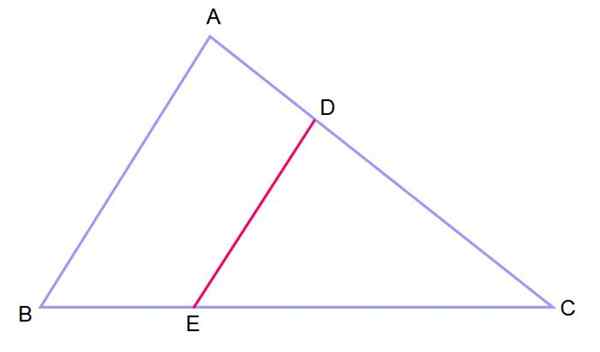Figur 3.- Två trianglar i positionen för sådana, med två parallella sidor och en gemensam vinkel, är liknande. Källa: f. Zapata.

När du har två trianglar ordnade på detta sätt sägs det att de är i en sådan position.

Ett förhållande mellan proportionalitet mellan segmenten höjs på samma sätt som för de parallella linjerna:

Vilket motsvarar denna andra, mellan motsvarande sidor av varje triangel, även kallad homologa sidor:

Var och en av dessa kvoter kallas likhetsskäl. I liknande trianglar är orsaken till likhet lika med kvoten mellan perimetrarna och kvadratet för likhetsförhållandet är lika med kvoten mellan områdena.

Därefter ett exempel där sådant teorem kan tillämpas på liknande trianglar och ta reda på hur mycket den okända sidan X är värd.

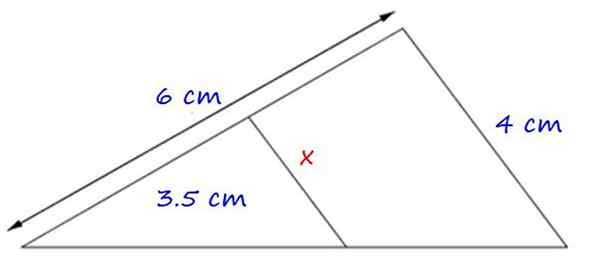Figur 4.- Tillämpningsexempel på det första sådana teorem. Källa: f. Zapata.

De bildade trianglarna är lika, eftersom de har en gemensam vinkel och sidorna x och 4 cm är parallella.

Därför är proportionaliteten mellan motsvarande sidor:

Och värdet på X rensas lätt:

x = (4 × 3.5) ÷ 6 cm = 2.3 cm

Andra satsen för detta

Detta sats hänvisar till en triangel vars vertikaler är punkter som tillhör en omkrets, vilket innebär att den är registrerad i den.

I detta fall konstaterar teoremet att när hypotenusa motsvarar diametern på omkretsen, är triangeln således spårad rektangel, det vill säga en av dess inre vinklar mäter 90º, som ses i figur 5 till vänster.

Kan tjäna dig: symbolisering av uttryck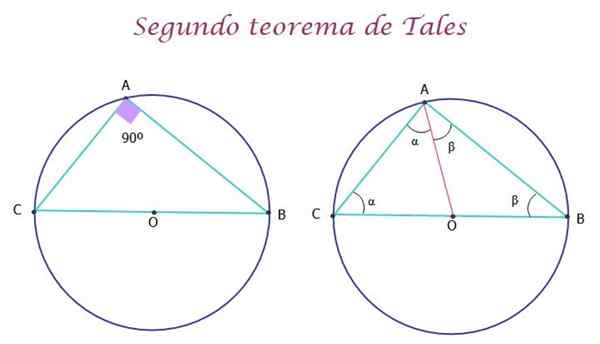Figur 5.- Den andra satsen för sådana säger att triangeln som är registrerad i omkretsen är rektangel. Källa: f. Zapata.

Demonstration av det andra teoremet för sådant

Demonstrationen av teoremet är mycket enkel. I figuren ovan har AO -segmentet ritats i rött, för att bilda de två AOC- och AOB -trianglarna, som är isosceler, eftersom sidorna OA, OC och OB är radioernas radioapparater och därför mäter de samma.

På detta sätt har trianglarna två lika vinklar, som är respektive α och ß. För den ursprungliga ABC -triangeln, som för alla triangel, uppfylls nu att summan av måtten på dess inre vinklar är lika med 180º, därför:

α + (α + β) + β = 180º

Därav:

2a + 2p = 180º

Därför:

2 (α +β) = 180º

α +β = 90º

Vilket bevisar att ABC -triangeln har en inre vinkel på 90º och därför är en rätt triangel.

Exempel

I följande figur är triangeln ABC isosceles och rektangel (isorektangel triangel), som är omkretsen av omkretsen lika med 25 cm. Hur mycket är AC- och AB -segmenten?

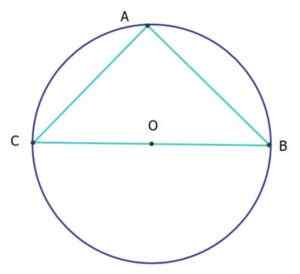
Omkretsen av omkretsen är dess längd l, ges beroende på dess diameter d med formel:

L = πd

Därför mäter diametern, som är CB -segmentet,:

D = CB = l/ π = 25 cm/ π = 7.96 cm.

Eftersom triangeln är liksikt, betyder detta att dess akuta vinklar mäter 45º vardera. Eftersom hypotenusen av triangeln är diametern för omkretsen, kan ett trigonometriskt förhållande på 45 användas, till exempel:

Sen 45º = AC/CB

AC = CB × sin 45º = 7.96 cm × sin 45º = 5.64 cm

Kan tjäna dig: Moivre -sats

AB -sidan har samma mått: 5.64 cm, eftersom triangeln är iSceles.

Sådana teoremapplikationer

Det första sådana teoremet kan användas för att veta avstånd som inte är lätt mätbara. Det sägs att sådana reste till Egypten och där bestämde på ett mycket genialt sätt höjden på den stora pyramiden.

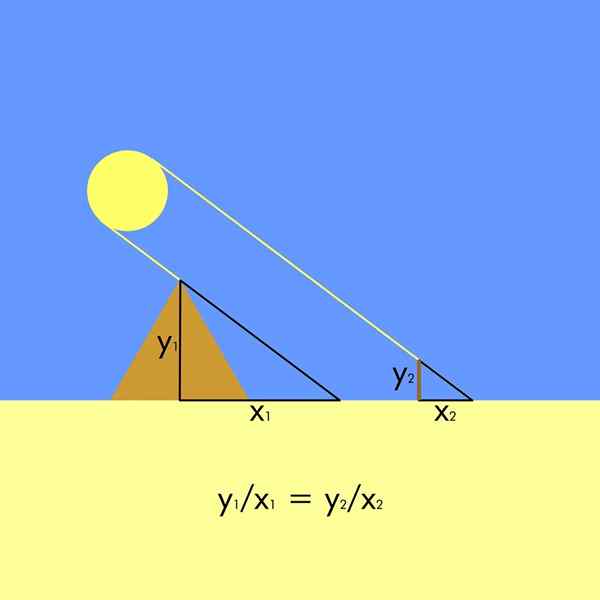
För detta var det nödvändigt. Således bildas två liknande trianglar, eftersom solens strålar har parallell incidens.

I figuren är höjden på pyramiden och₁ Och hans skugga är x₁, Medan höjden på insatsen är och₂ (Vissa kroniker hävdar att sådan använde sin egen höjd) och deras skugga är x₂. Eftersom trianglarna är liknande bildas följande proportionalitetsförhållande:

Att vara väldigt lätt att rensa höjden på pyramiden och₁:

och₁ = x₁∙ (och₂ ÷ x₂)

Referenser

1. Alexander, D. 2013. Geometri. Femte. Utgåva. Cengage Learning.
2. Requena, b. En sådan teorem. Återhämtat sig från: universalformulor.com.
3. Matematisk hall. Tales de Mileto och den stora pyramiden. Hämtad från: salonmatematisk.com
4. Superprof didaktiskt material. Miletus sådan. Återhämtat sig från: superprof.är.
5. Thales och likhetssats. Två mycket gamla problem. Återhämtat sig från: edu.Xunta.Tjej.