Teselados karakteristik, typer (vanliga, oregelbundna), exempel

De Tesselled De är ytor täckta av en eller flera figurer som kallas Tessels. De finns överallt: på gator och byggnader av alla slag. Tessels eller plattor är platta bitar, vanligtvis polygoner med kongruenta eller isometriska kopior, som placeras efter ett regelbundet mönster. På detta sätt finns det inga utrymmen utan att täckas och plattorna eller mosaikerna överlappar inte. 

I det fall att en enda typ av mosaik som bildas av en vanlig polygon används så finns det en vanlig Tesseld, Men om två eller flera typer av vanliga polygoner används, är det en Semi -regelbunden tesselled.

Figur 1. Oregelbundet golvgolv, eftersom rektanglar är icke-regelbundna polygoner, även när rutorna är. Källa: Pixabay.

Slutligen när polygonerna som bildar Tesseldo inte är regelbundna, så är det en oregelbunden tessell.

Den vanligaste typen av Tesseldo är den som bildas av rektangulära och särskilt fyrkantiga mosaiker. I figur 1 har vi ett bra exempel.

[TOC]

Teselados historia

Tessellation har använts i tusentals år för att täcka golv och väggar i palats och tempel med olika kulturer och religioner.

Till exempel den sumeriska civilisationen som blomstrade omkring 3500 till.C. Söder om Mesopotamia, mellan Eufrat och Tigris floder, använde de tesels i sin arkitektur.

figur 2. Teselados Sumerios vid dörren till Istar. Källa: Wikimedia Commons.

Teslarna har också väckt intresset för matematiker från alla tider: Börjar med Archimedes under det tredje århundradet f.Kr.

Det kan tjäna dig: fraktion motsvarande 3/5 (lösning och förklaring)

Penrose skapade en icke -periodisk tessellation känd som Penrose Tessellation. OCHdessa De är bara några namn på forskare som bidrog mycket om tessellation.

Vanliga teslar

Regelbunden teslat tillverkas med en enda typ av vanlig polygon. Å andra sidan, så att Tesseldo kan betraktas som regelbundet, måste hela planet:

-Tillhör polygoninredningen

-Eller till kanten av två angränsande polygoner 

-Slutligen kan det tillhöra det vanliga toppen av minst tre polygoner.

Med ovanstående begränsningar kan det demonstreras att endast de liksidiga trianglarna, rutorna och hexagonerna kan bilda ett vanligt tessel.

Nomenklatur

Det finns en nomenklatur för att beteckna de teslar som består av listan i riktning mot klocknålarna och separeras med en punkt, antalet sidor av polygonerna som omger varje nod (eller toppunkt) för de tessellerade, alltid börjar med det minsta antalet av sidorna.

Denna nomenklatur gäller regelbundna och semi -regelbundna tesselves. 

Exempel 1: Triangulär Teselado

Figur 3 visar en triangulär regelbunden kakel. Det bör noteras att varje triangulär kakelnod är det vanliga toppen av sex liksidiga trianglar. 

Vägen att beteckna denna typ av Tesseldo är 3.3.3.3.3.3, som också betecknas av 3⁶.

Figur 3. Triangulär vanlig Teselado 3.3.3.3.3.3. Källa: Wikimedia Commons

Exempel 2: Square Tessel

Figur 4 visar en regelbunden kakel som endast består av rutor. Det bör noteras att varje kakelnod är omgiven av fyra kongruenta rutor. Notationen som gäller för denna typ av fyrkantiga Tesselves är: 4.4.4.4 o växelvis 4⁴

Figur 4. Square Tesseld 4.4.4.4. Källa: Wikimedia Commons.

Exempel 3: Hexagonal Tesseld

I en hexagonal tesselle. Nomenklaturen för en vanlig hexagonal tesselled är 6.6.6 o växelvis 6³.

Kan tjäna dig: koniska avsnitt: Typer, applikationer, exempel Figur 5. Hexagonal Tesseld 6.6.6. Källa: Wikimedia Commons.

Semi -regelbunden tesselled

Semi -regelbundna eller tesselled teslar av Archimedes består av två eller flera typer av vanliga polygoner. Varje nod är omgiven av de typer av polygoner som utgör de tessellerade i samma ordning och villkoret för en kant som är helt delad med grannen upprätthålls.

Det finns åtta halvregulära teslar:

1. 3.6.3.6 (tri-hexagonal tesselled)
2. 3.3.3.3.6 (Hexagonal Teslate Romo)
3. 3.3.3.4.4 (Elongado Triangular Teselado)
4. 3.3.4.3.4 (Romo Square Tesselled)
5. 3.4.6.4 (Rombi-Tri-hexagonal Tesseld)
6. 4.8.8 (trunkerad fyrkantig tesselled)
7. 3.12.12 (trunkerad hexagonal tesseld)
8. 4.6.12 (trunkerad tri-hexagonal tesseld)

Några exempel på semi -regelbundet teslat visas nedan.

Exempel 4: Tixagonal Teselado

Det är den som består av regelbundna liksidiga trianglar i struktur 3.6.3.6, vilket innebär att en kakelnod är omgiven (tills den är klar en avkastning) av en triangel, en hexagon, en triangel och en hexagon. Figur 6 visar en sådan tessel.

Figur 6. Tri-hexagonal Tesseld (3.6.3.6) Det är ett exempel på semi -regelbundet tesselled. Källa: Wikimedia Commons.

Exempel 5: Hexagonal Tesseldo Romo

Liksom plattan i föregående exempel består detta också av trianglar och hexagoner, men dess distribution runt en nod är 3.3.3.3.6. Figur 7 illustrerar tydligt denna typ av tesselled.

Figur 7. Den hexagonala Tesseldo Romo består av en hexagon omgiven av 16 trianglar i konfiguration 3.3.3.3.6. Källa: Wikimedia Commons.

Exempel 6: Rombi-Tri-hexagonal Tessel

Det är en kakel som består av trianglar, rutor och hexagoner, i konfiguration 3.4.6.4, som visas i figur 8.

Figur 8. Semi -regelbunden tesselled sammansatt av en triangel, en fyrkant och en hexagon i konfiguration 3.4.6.4. Källa: Wikimedia Commons.

Oregelbundna teslar

De kallas oregelbundna teslar till de som bildas av oregelbundna polygoner, eller av vanliga polygoner, men som inte uppfyller kriteriet att en nod är ett toppunkt på minst tre polygoner.

Det kan tjäna dig: antiderivativ: formler och ekvationer, exempel, övningar

Exempel 7

Figur 9 visar ett exempel på oregelbundna plattor, där alla polygoner är regelbundna och kongruenta. Det är oregelbundet eftersom en nod inte är ett vanligt toppunkt på minst tre rutor och det finns också angränsande rutor som inte helt delar en kant.

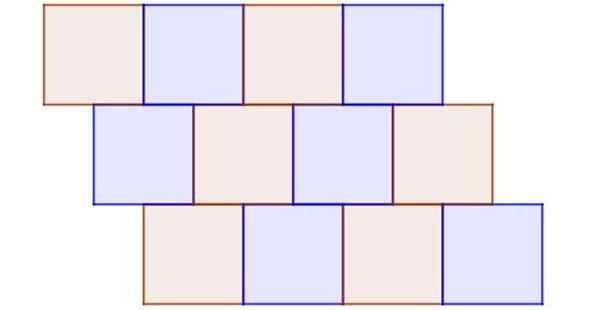Figur 9. Även när alla plattor är kongruenta rutor är detta ett tydligt exempel på oregelbundna tesselled. Källa: f. Zapata.

Exempel 8

Parallellogrammet tees en plan yta, men såvida det inte är en fyrkant kan inte bilda en vanlig tessel.

Figur 10. En Tesseldo som bildas av parallellogram är oregelbundet, eftersom dess mosaiker är icke -regulära polygoner. Källa: f. Zapata.

Exempel 9

Icke-regelbundna hexagoner med central symmetri sätter en plan yta, som visas i följande figur:

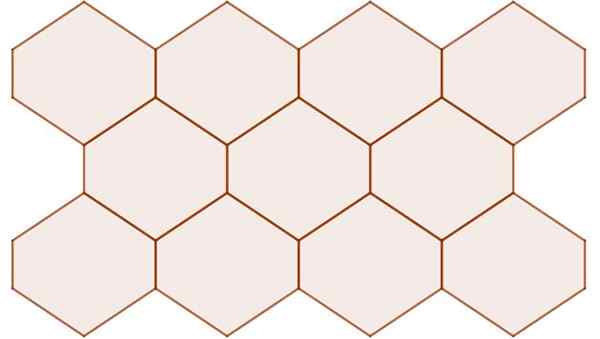Figur 11. Hexagoner med central symmetri även när de inte är regelbundna sätter de planen. Källa: f. Zapata.

Exempel 10: El Cairo Teselado

Det är en mycket intressant tessellation, sammansatt av pentagoner med sidor av samma längd men med ojämlika vinklar, varav två är raka och de tre andra har 120º vardera.

Hans namn kommer att denna Tesseld är i trottoaren på några av gatorna i Kairo i Egypten. Figur 12 visar Tesseldo från Kairo.

Figur 12. Kairo Tesseldo. Källa: Wikimedia Commons.

Exempel 11: Teselado al-Andalus

Tesseldo under vissa delar av Andalusien och Nordafrika kännetecknas av geometri och epigrafi, utöver prydnadselement som vegetation. 

Palacios's tesselled som Alhambra som består av plattor som bildas av keramiska bitar i många färger, med flera (för att inte säga oändliga) former som utlöste geometriska tomter.

Figur 13. Teselado Palacio de la Alhambra. Tartaglia / allmän domän

Exempel 12: Teselado i videogorna

Även känd som Tesellation, det är en av de mest boom i videospel. Detta är skapandet av strukturer för att simulera tesseld av de olika scenarierna som visas i simulatorn.

Detta är den tydliga reflektionen som dessa omslag fortsätter att utvecklas genom att överföra verklighetens gränser.

Referenser

1. Njut av matematik. Tesel. Återhämtat sig från: njutmatimaticas.com
2. Rubiños. Tesels Löst exempel. Återhämtat sig från: matematik.Bloggfläck.com
3. Weisstein, Eric W. "Deiregula Tessellation". Weisstein, Eric W, ED. Matematik. Wolfram Research.
4. Wikipedia. Tesselled. Återhämtad från: är.Wikipedia.com
5. Wikipedia. Vanlig Tesseld. Återhämtad från: är.Wikipedia.com