Tetradecágono

Vad är en tetradecágono?

Tetradecágono är en platt och stängd geometrisk figur på 14 sidor som tillhör Polygons -familjen. Det är också känt med namnet på tetrakaidecágono, Alla ord härrörande från grekiska ord: "tetra" (cuatri), "kai" (mer), "förfall" (tio) och "gon" (vinkel), eftersom det också har 14 inre vinklar.

Figuren visar en regelbunden tetradagon, det vill säga en vars sidor och inre vinklar har alla samma mått, som visar de viktigaste egenskaperna hos denna figur.

Figur 1.- Regelbunden tetrade med sina huvudsakliga egenskaper. Källa: f. Zapata.

Tetradecágono -element

• Sidor: De kallas de 14 linjesegmenten som är stängda för att bilda figuren. De kan alla ha samma längd, i vilket fall polygonen är regelbunden, eller så kan de vara annorlunda och sedan finns det en oregelbunden tetrade.
• Häckar: De är korsningspunkterna mellan på varandra följande segment och Tetradecágono har 14 vertikaler.
• Centrum: Equidistant Point of the Vernices.
• Radio: segment som förenar centrum med ett toppunkt.
• Inre vinkel: Det bildas av figurens insida och mellan två på varandra följande eller angränsande segment. Åtgärder 154.286º för den vanliga Tetradecágon, oavsett sidans storlek.
• Yttre vinkel: bildas mellan ena sidan och förlängningen av en av de angränsande sidorna. Oavsett sidolängd mäter denna vinkel 25.7143º för en vanlig tetrade.
• Centralvinkel: Den som har sitt toppunkt sammanfaller med mitten av polygonen och dess sidor är två på varandra följande radioapparater.
• Diagonal: segment som ansluter två icke -konsekutiva hörn.

Hur är en tetradecágono?

De vanliga polygonerna av N -sidor som är byggda med regel och kompass har en n av formen 2^r p₁... P_k, vara p_Yo Fermat Primo -nummer olika, och i sin tur tar Fermats primnummer form 2ⁿ + 1.

Kan tjäna dig: i väntan på en linje: formel och ekvationer, representation, exempel

Tetradecágono har n = 14 sidor, men 14 = 7 × 2, som inte är fermatkusiner, eftersom de inte kan uttryckas på det angivna sättet. Därför medger denna polygon inte exakt konstruktion med regel och kompass, utan en konstruktion som närmar sig mycket bra genom flera metoder.

Allmän metod för att bygga regelbundna polygoner

Följande är en allmän metod (inte den enda) som bygger regelbundna polygoner som är registrerade i en omkrets, inklusive den vanliga tetrade.

Den består av att dela den vertikala diametern för denna omkrets i så många lika delar som sidor har polygonen att rita. När det gäller Tetradecágono kommer de att vara de 14 delarna numrerade i bild 2. Det här är stegen:

• Rita en vertikal diameter från A till B.
• Rita sedan en semi -rätt från och med punkt A, öppna kompassen med godtycklig öppning och gör 14 lika fördelade divisioner om det. SemirRect och dess divisioner kan komma ur omkretsen.
• Gå med i 14VA -märket (i blått i bilden) i slutet av semi -rätten med punkt B.
• För att fortsätta att gå med i resten av märkena i semi -rekreation med respektive punkter på den vertikala diametern (gröna punkter).
• Med kompassens spets i A och öppning lika med måttet på diametern på omkretsen en båge ritas. Med samma mått, men som stöder spetsen i B (punkt 14 i figur 2) dras en annan båge, som skärs med den första vid punkter V och V '.

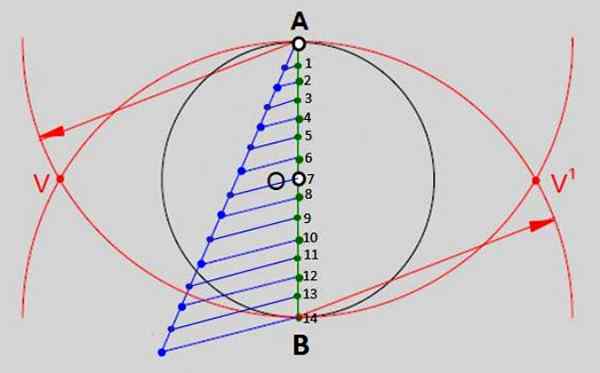figur 2.- En av de allmänna metoderna för att bygga regelbundna polygoner är att dela upp diametern i omkretsen i så många lika delar som sidor har polygonen. När det gäller vanlig tetradech finns det 14 lika delar. Källa: f. Zapata.

• Nu, med regeln, rita en linje från V 'till punkt 2 och förlänga den för att korsa omkretsen vid punkt C i figur 3. Markera skärningspunkten, som kommer att vara en av vertikalerna i figuren.

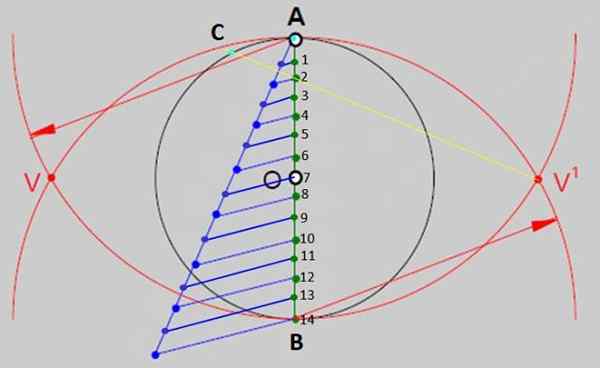Kan tjäna dig: statistikgrenar Figur 3.- AC -segmentet är måtten på sidorna på den byggda tetradecion. Källa: f. Zapata.

• Öppna kompassen på AC -avståndet och stödja spetsen i A eller C, rita bågar med lika mått över hela omkretsen, på detta sätt är det uppdelat i ungefär lika delar, skärningspunkten mellan bågarna och omkretsen är vertikalerna är de toppar av tetradecágono.
• Med en regel, gå med i topparna med linjesegment och bildar sidorna på polygonen.
• Radera noggrant hjälpkonstruktioner.

I följande animation visas en annan ungefärlig metod, med regel och kompass:

Figur 4.- Animering som visar hur en Tetradecágon görs (ungefär vanlig polygon). Källa: Wikimedia Commons.

Formler för regelbunden tetrade

Följande formler är giltiga för vanliga polygoner:

• Arknummer: n
• Sidmått: a
• Apothem: l_TILL
• Radio: R
• Omkrets: P
• Område: a
• Intern vinkel: i
• Extern vinkel: E
• Diagonal: D

Känd sida till apotemet

A = 2l_TILL × tg (π/n)

För n = 14:

A = 2l_TILL × TG (π/14)

Känd sida radion

A = 2r × sen (π/n)

Ja n = 14:

A = 2R × SEN (π/14)

Känd omkrets sidan

Omkretsen är summan av sidorna. När Tetradecágono är regelbunden:

P = n⋅a = 14⋅a

Om tetradecágono är oregelbunden måste alla sidor läggas direkt till för att få omkretsen.

Känt område sidan

A = ¼ na² × barnsäng (π/n)

För n = 14:

A = ¼ (14: e²) × barnsäng (π/14) = (7/2) a² × barnsäng (π/14)

Känt område

A = n⋅l_TILL ² × tg (π/n)

Tar n = 14 resultat:

A = 14L_TILL ² × TG (π/14)

Område baserat på omkretsen och apotemet

A = (p × l_TILL)/2

Kan tjäna dig: Bayes teorem

Inre vinkelmått

 När n = 14 mäter den inre vinkeln för tetradecágono i grader:

I = 12 × 180º /14 = 154.286º

Yttre vinkelmätning

E = 360º/N

När n = 14 har du:

E = 25.7143º

Diagonaler

Formeln för att beräkna antalet diagonaler som finns i någon polygon, regelbunden eller inte, är:

För n = 14:

D = 14 × 11/2 = 77 diagonaler

Exempel

Ett annat exempel på Tetradecágon

Regelbundna polygoner förekommer upprepade gånger i många mönster, till exempel valutor. När det gäller regelbunden tetradagon visas detta i malaysiska minnesmynt, som representerar dess sidor till var och en av de fjorton konfedererade staterna i den nationen.

Konkav och konvex tetradecágonos

I allmänhet kan polygoner som tetradecágono vara konvexa eller konkava, i det första fallet överstiger måttet på deras inre vinklar inte 180º. Den vanliga tetradech är konvex, som alla vanliga polygon, eftersom någon av dess inre vinklar mäter 154.286º.

Å andra sidan, i den konkava tetradech, mäter en eller flera av dess inre vinklar mer än 180º.

Numeriskt exempel

Med tanke på en vanlig tetradagon vars sida mäter 5 cm, hitta:

a) omkrets
b) apotemmätning
c) radiolängd
d) område

Svar

a) Eftersom det är en vanlig polygon är omkretsen:

P = 14 × 5 cm = 70 cm.

b) Från ekvation A = 2L_TILL × tg (π/14), där a = 5 cm, apotem l_TILL:

L_TILL = a / [2 × tg (π / 14)] = 5 cm / 0.4565 = 21.9064 cm

C) Radio R kan beräknas med a = 2r × SEN (π/14):

R = a / [2 × sin (π / 14)] = 5 cm / 0.4565 = 22.4698 cm

d) Det finns flera alternativ för området, till exempel a = (p × l_TILL)/2:

A = (70 × 21.9064)/2 cm² = 1533.45 cm².

Referenser

1. Alexander, D. 2013. Geometri. Femte. Utgåva. Cengage Learning.
2. Arturogeometri. Allmän metod för att rita polygoner som är inskrivna i omkretsar. Återhämtat sig från YouTube.com
3. Soppkalkylator. Vanlig polygonkalkylator. Återhämtat sig från: kalkylatorosoup.com.
4. Teckning. Regelbundna polygoner. Återhämtad från: ritning.com.
5. Requena, b. Konkav polygon. Återhämtat sig från: universalformulor.com.
6. Wikipedia. Byggbar polygon. Återhämtad från: är.Wikipedia.org.