Typer av funktioner och deras grafer

- 5029
- 1419
- Per Eriksson
Det finns olika Typer av funktioner som används för att modellera problem inom kunskapsgrenar som naturvetenskap, administration, ekonomi och samhällsvetenskap. Matematiskt sett är en funktion en relation mellan två eller flera variabler.
Många gånger är vissa objekt eller mängder relaterade till varandra. Dessa mängder representeras av variabler. Till exempel finns det två relaterade variabler som tillhör två uppsättningar A och B, inte nödvändigtvis numeriska, även om de flesta är-.
För att betraktas som en funktion måste detta förhållande uppfylla två villkor: det första är att alla element i startuppsättningen ska delta, och den andra, att varje element i nämnda uppsättning är relaterade till endast ett av elementen i uppsättningen B.
Variabler kallas vanligtvis med bokstäver x och och, med x som den oberoende variabel och och som den beroende variabel. Naturligtvis kan de kallas på något annat sätt och välja namnet på variabeln i enlighet med den storlek som den representerar.
Förhållandet mellan de två betecknas genom brevet F -eller en annan bokstav i alfabetet, och representeras på flera sätt, till exempel en uppsättning ordnade par, en graf, ett verbalt uttryck eller en algebraisk formel:
- f (x) = x + 1
- Befolkning p i en viss stad i ett visst tidsintervall t.
- H (x) = (1,3); (2,4); (3,5); (4.6)
Funktioner kännetecknas av att ha domän och räckvidd eller rutt. Domän är den uppsättning värden som variabeln x Du kan ta, medan sortimentet är uppsättningen värden som förvärvar den beroende funktionen eller variabeln och.
Klassificering av funktioner
Funktionerna kan grupperas i 5 stora kategorier, vilket återspeglas i följande schema, där varje grupp är märkt med ett romerskt nummer och en färg. Från och med vänster till höger klassificeras funktionerna enligt:
- I) dess form.
- Ii) symmetri.
- Iii) sättet att uttrycka variabeln.
- Iv) dess kontinuitet och monotoni.
- V) hur domänelementen är relaterade till de i sortimentet.
 Huvudklassificeringskriterier för funktioner. Källa: f. Zapata.
Huvudklassificeringskriterier för funktioner. Källa: f. Zapata. Följ nu en kort beskrivning av var och en av de typer av funktioner med deras respektive exempel.
I) fungerar enligt dess form
Yo.1) Algebraiska funktioner
De är bland de mest använda funktionerna inom många vetenskapsområden, och därför är de de mest kända. De kännetecknas av att ha en korrespondensregel, ett algebraiskt uttryck.
I sin tur delas algebraiska funktioner i följande typer:
- Yo.1.a) Polynom eller polynom.
- Yo.1.b) rationell.
- Yo.1.c) irrationell.
- Yo.1.d) efter sektioner.
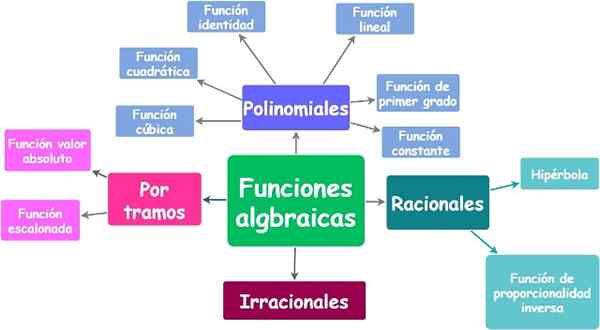 Algebraiska funktioner och deras typer. Källa: f. Zapata.
Algebraiska funktioner och deras typer. Källa: f. Zapata. Yo.1.a) Polynom- eller polynomfunktioner
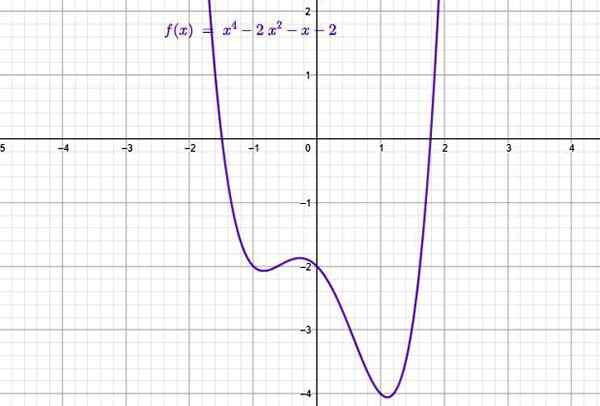 Exempel på polynomtypfunktion. Källa: f. Zapata genom geogebra.
Exempel på polynomtypfunktion. Källa: f. Zapata genom geogebra. De består av summor vars allmänna form är:
P (x) = anxn + till N-1xN-1 +Till ... till1x + a0
Där koefficienterna tilln, till N-1Till ... till1, till0 De är verkliga siffror och n är ett heltal. Domänen för polynomfunktioner är uppsättningen för verkliga siffror och är också kontinuerliga funktioner i hela den domänen.
I den övre figuren finns grafen för följande polynomfunktion i ordning 4:
f (x) = x4 - 2x2 - x -2
Bland polynomfunktionerna kännetecknas vissa speciella fall, enligt koefficienternas värden. Det är värt att överväga noggrant, eftersom de är mycket användbara i flera situationer:
i) konstant funktion
Det finns en konstant funktion när alla koefficienter avbryts, utom0:
f (x) = a0 = k
Grafen för konstantfunktionen är en rak linje parallell med den horisontella axeln, såsom linjer:
- f (x) = 2
- g (x) = π
- H (x) = -3/2
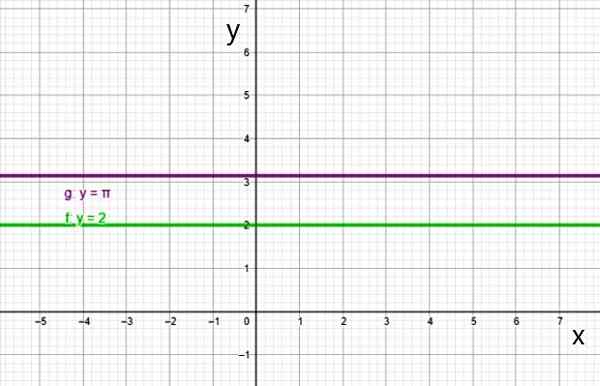 Två exempel på konstant funktion. Källa: f. Zapata.
Två exempel på konstant funktion. Källa: f. Zapata. Ii) First Degree Function
Den första graden -funktionen eller relaterad funktion är den vars graf är en rak linje. Det är ett särskilt fall av polynomfunktionen där alla koefficienter för ogiltigförklaring1 redan0. Det ges av:
f (x) = a1x + a0
Värdet a1 Det är linjens lutning, som ger ett mått på dess lutning, och0 Det är snittet av linjen med den vertikala axeln. Båda kan ta positiva eller negativa värden.
Exempel på första gradsfunktion är följande:
- G (x) = 2x -1
- H (x) = -6x +5/2
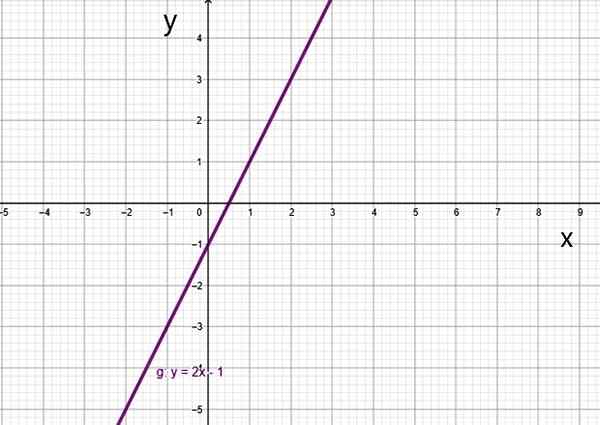 Första gradsfunktionen f (x) = 2x-1. Källa: f. Zapata.
Första gradsfunktionen f (x) = 2x-1. Källa: f. Zapata. Det finns ett speciellt fall, som är den linjära funktionen.
Kan tjäna dig: centrala tendensåtgärder för grupperade data: formler, övningariii) linjär funktion
När koefficienten för0 Det är 0, funktionen går alltid genom ursprunget och uttrycks av f (x) = a1X, ringer linjalfination, Hur mår du:
- f (x) = 5x
- G (x) = -7x
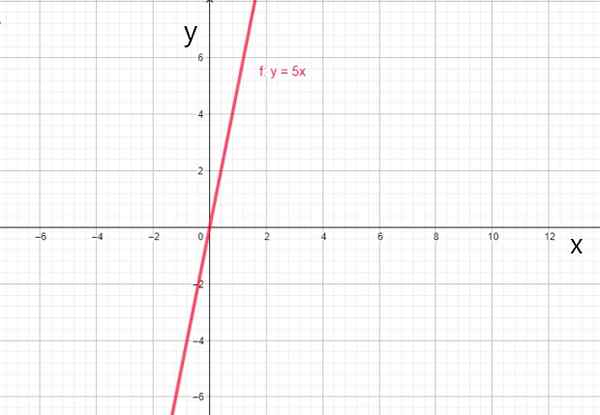 Linjär funktion f (x) = 5x. Källa: f. Zapata.
Linjär funktion f (x) = 5x. Källa: f. Zapata. iv) identitetsfunktion
Det är ett särskilt fall av den linjära funktionen, där1 = 1:
f (x) = x
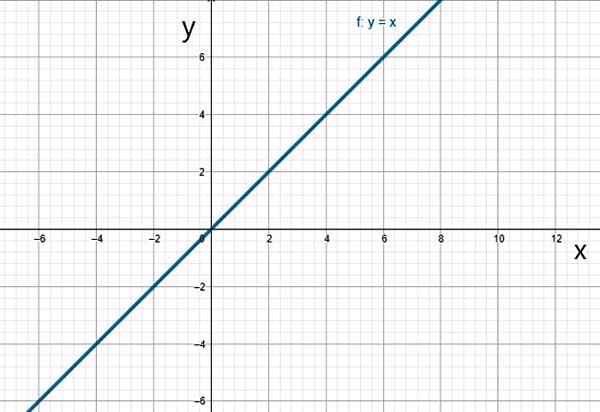 Identitetsfunktionen. Källa: f. Zapata.
Identitetsfunktionen. Källa: f. Zapata. v) kvadratisk funktion
Den har den allmänna formen:
f (x) = a2x2 +till1x + a0
Med en2 ≠ 0.
Dess graf är en liknelse vars axiella eller symmetriaxel är parallell med ordinatens axel. Korsar alltid den vertikala axeln vid koordinatpunkten x = 0, y = a0. När det gäller korsningar med den horisontella axeln kan den ha upp till maximalt 2.
Exempel på kvadratiska funktioner är:
- f (x) = x2 - 3x - 4
- G (x) = 4x2
- H (x) = x2-1
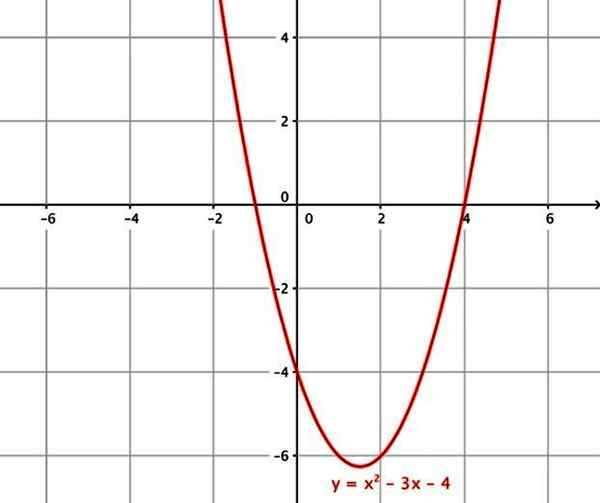 Den kvadratiska funktionen. Källa: Wikimedia Commons.
Den kvadratiska funktionen. Källa: Wikimedia Commons. vi) kubikfunktion
Som namnet antyder innehåller den kubiska funktionen en effekt på 3:
f (x) = a3x3 + till2x2 + till1x + a0
Koefficienten a3 Det skiljer sig alltid från 0, som i dessa fall:
- f (x) = x3
- G (x) = 5x3 - 2
- H (x) = -3x3 + 4x2 + 10x + 1
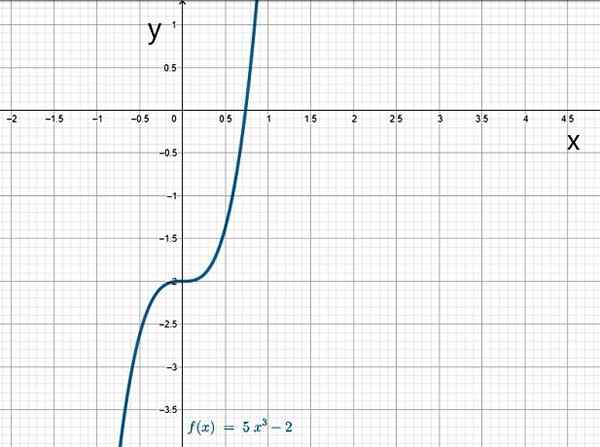 Kubikfunktion. Källa: f. Zapata.
Kubikfunktion. Källa: f. Zapata. Yo.1.b) rationella funktioner
Rationella funktioner har formen:
=\fracP(x)Q(x))
Från domänen för rationella funktioner, alla värden som ogiltigförklarar nämnaren Q (x), det vill säga dess rötter, medan värdena på värdena på värdena på och som bestämmer de horisontella asymptoterna.
En asymptot är en linje som funktionen närmar sig, både till vänster och till höger, över eller under, men aldrig korsar. Sådana linjer kan vara vertikala, horisontella eller benägna.
Exempel på rationella funktioner är:
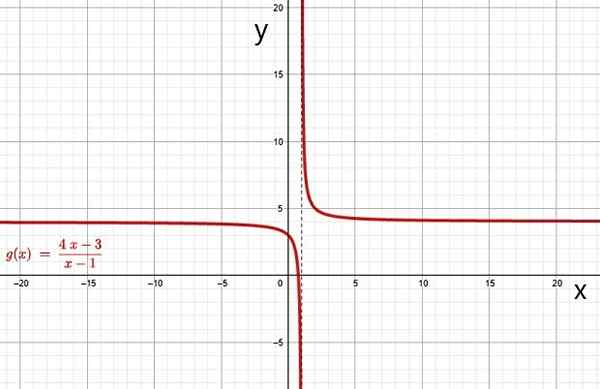 Rationell funktion. Källa: f. Zapata genom geogebra.
Rationell funktion. Källa: f. Zapata genom geogebra. i) Hyperbola
Grafen för en rationell funktion är en hyperbola när polynom i nämnaren Q (X) har klass 1. Grafen över funktionerna f (x) och g (x) för exemplen ovan är hyperbolor, det kan enkelt kontrolleras genom en gratis grafikprogramvara, till exempel Geogebra.
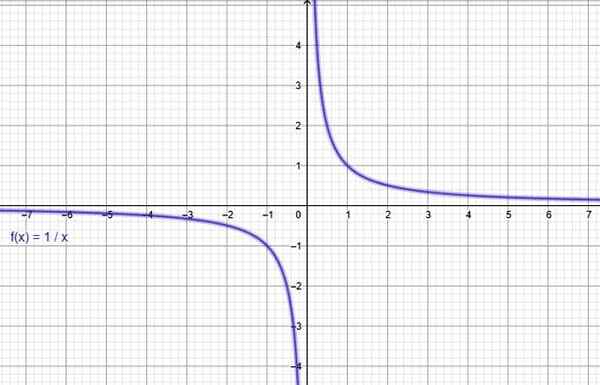 Funktionen y = 1/x. Källa: f. Zapata genom geogebra.
Funktionen y = 1/x. Källa: f. Zapata genom geogebra. Ii) omvänd proportionalitetsfunktion
Det är en funktion av form:
Där C är ett verkligt antal annorlunda än 0. Dess domän är uppsättningen av verkliga siffror förutom 0.
Yo.1.c) irrationella funktioner
Är de vars oberoende variabel är under ett radikalt tecken. Dess allmänna form är:
Vissa av dessa funktioner kan vara:
Domänen för dessa funktioner bestäms enligt följande:
-Om rötterna är av vridmomentindex måste den subradiska mängden f (x) alltid vara 0 eller positiv.
-När rötterna är udda kan f (x) vara positiva eller negativa. Därför är funktionen i detta fall de verkliga siffrorna.
Till exempel domänen för:
Det är uppsättningen av verkliga siffror så att X-3 är större än eller lika med 0. I detta fall måste X vara större än eller lika med 3. Därför är domänen för denna funktion uppsättningen av värden för intervallet [3, ∞+).
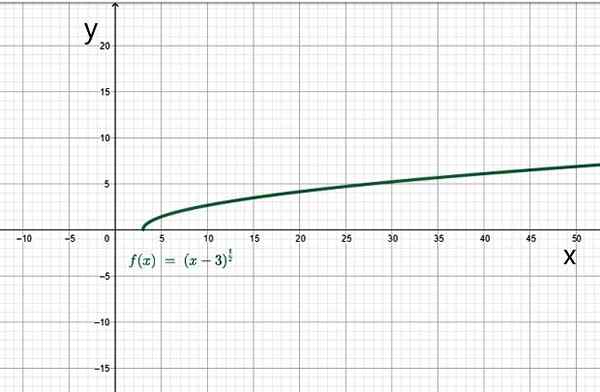 Exempel på irrationell funktion. Källa: f. Zapata.
Exempel på irrationell funktion. Källa: f. Zapata. Yo.1.d) Funktioner i bitar eller efter sektioner
Funktionen i delar, efter sektioner eller delar är en som kräver mer än en formel för olika domänvärden. Här är några exempel på din ansökan:
-Priser för att skicka paket per post, beroende på vikt eller volym, ursprung och destination för samma.
-Priser för tjänster, till exempel telefoni och el.
-Försäljning av biljetter till museer eller nöjesparker, beroende på ålder.
I matematisk form kan en funktion i delar till exempel vara:
Domänen för en funktion i delar beror på dess definition. I föregående exempel är domänen uppsättningen som bildas av: (-∞, -1) ∪ [1,+∞).
Ii) Escalonada -funktion
Grafen över denna funktion av avsnitt består av steg, till exempel en stege eller kan vara av olika höjder, beroende på hur funktionen definieras.
Det kan tjäna dig: Hipparco of Nicea: Biografi och bidrag till vetenskapenFör detta väljs ett ändligt intervall [a, b] som innehåller ett visst ändligt antal diskontinuiteter, kallad xYo < x1 < x2 <… . xn Och ett öppet intervall väljs (xYo , xI+1) Att ge det en konstant av värde sYo, Med hopp på punkter xYo. Värdet på sYo Det är höjden på steget i fråga.
Ett exempel på en förskjuten funktion är hela delen, som tar valfritt nummer och associerar det med följande heltal, antingen av överskott eller som standard. Följande är en hel del:
[x] = (större heltal ≤ x)
Enligt denna funktion, hela delen av 2.5 är:
[2.5] = (större heltal ≤ 2.5) = 2
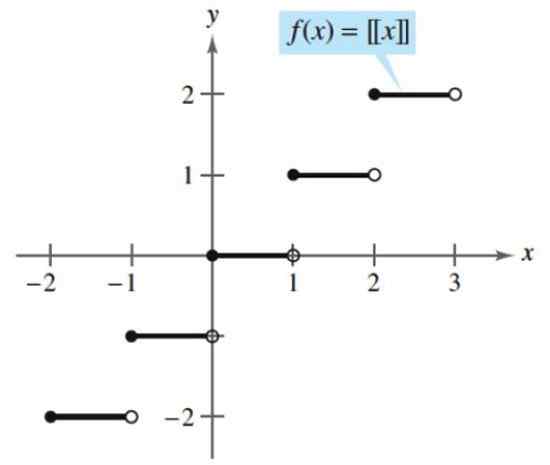 Hela delen av. Källa: Larson, R. Beräkning med analytisk geometri. McGraw-hill.
Hela delen av. Källa: Larson, R. Beräkning med analytisk geometri. McGraw-hill. Yo.2) transcendenta funktioner
Icke -algebraiska funktioner kallas transcendent. De exponentiella, logaritmiska och trigonometriska funktionerna är transcendenta funktioner.
I dem variabeln x Det är en del av argumentet om funktionen eller som en del av exponenten eller indexet för någon rot, till exempel:
- f (x) = log (x+1)
- H (x) = -0.2⋅8-3x
Transcendenta funktioner har många tillämpningar, till exempel i studien av vibrationer och vågor, sannolikhetsfördelningar, modellering av vågorna, tillväxten av olika populationer, radioaktivt förfall, räntor och många fler.
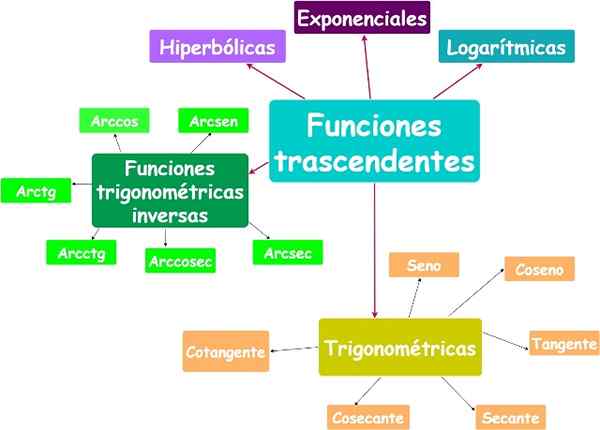 Huvudtranscendentfunktioner. Källa: f. Zapata.
Huvudtranscendentfunktioner. Källa: f. Zapata. Yo.2.a) exponentiell funktion
Exponentiell funktion definieras av:
f (x) = ax
Där A är basen, som alltid är ett positivt antal på 1, och variabeln, ett verkligt nummer, visas i exponenten. I allmänhet skrivs den exponentiella funktionen:
f (x) = a⋅aBx
Här är A och B verkliga koefficienter. Följande är funktioner av denna typ:
- f (x) = 5ex
- H (x) = 4. 105x
- g (t) = 8e-2t
Bas och, var och Det är antalet Euler 2.71828 ..., visas ofta i problem med vetenskap och teknik samt statistik. När funktionen har den här basen kallas Naturlig exponentiell funktion.
Domänen för den exponentiella funktionen är uppsättningen av verkliga siffror, medan intervallet är de positiva siffrorna.
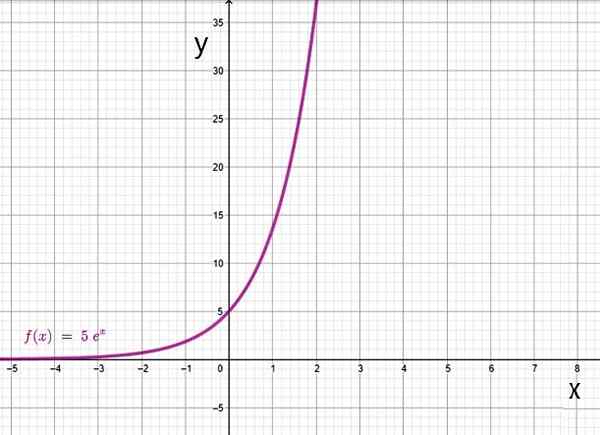 Exponentiell funktion baserad på. Källa: f. Zapata genom geogebra.
Exponentiell funktion baserad på. Källa: f. Zapata genom geogebra. Yo.2.b) logaritmfunktion
Logaritm -funktionen baseras på sin sida till Det är den omvända funktionen för den exponentiella funktionen baserad på till. Ja:
loggatill x = y
Så:
x = aoch
Speciellt, om basen för logaritmen är nummer E, kallas funktionen Neperian logaritmfunktion Och det betecknas som ln. Funktioner av denna typ är:
- f (x) = ln x
- g (x) = log (x+1)
- H (t) = 1 - log x2
Domänen för logaritmfunktionen, oavsett bas, är de positiva verkliga siffrorna, inklusive 0. Det vill säga, det finns inga logaritmer med negativa siffror eller 0.
En logaritm kan emellertid vara 0 eller negativ: logaritmen för numret mellan 0 och 1 är negativ och för sin del uppnårtill 1 = 0.
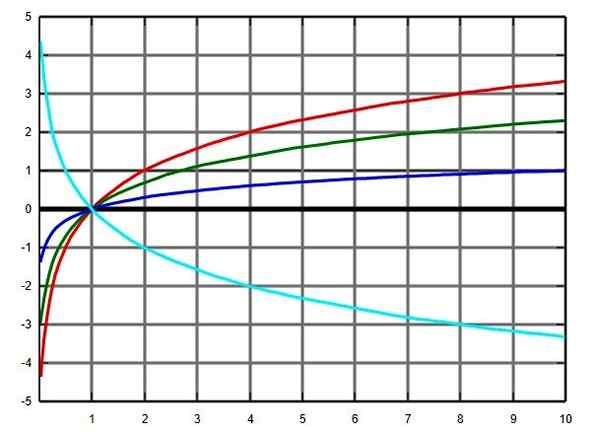 Logaritmfunktionsgraf i flera baser: bas 2 i rött, grönt E, blå -bas och turkos på bas 0.5. Källa: Wikimedia Commons.
Logaritmfunktionsgraf i flera baser: bas 2 i rött, grönt E, blå -bas och turkos på bas 0.5. Källa: Wikimedia Commons. Yo.2.c) trigonometriska funktioner
De är de som kommer från de trigonometriska skälen: sinus, kosinus, tangent, torkning, harmoning och cotangent av en vinkel x. De betecknas respektive:
Sen x, cos x, tg x, sek x, skada x och cotg x
De är periodiska funktioner, vilket innebär att dess form är repetitiva, så de är mycket användbara för att beskriva naturfenomen som signaler, svängningar, cirkulär rörelse och svängrörelser, som kännetecknas av att vara repetitiva.
Exempel på trigonometriska funktioner är:
- f (x) = sin x
- G (t) = 5⋅COS (ωt + π)
- H (x) = tg (x/2)
Variabel X uttrycks i radianer.
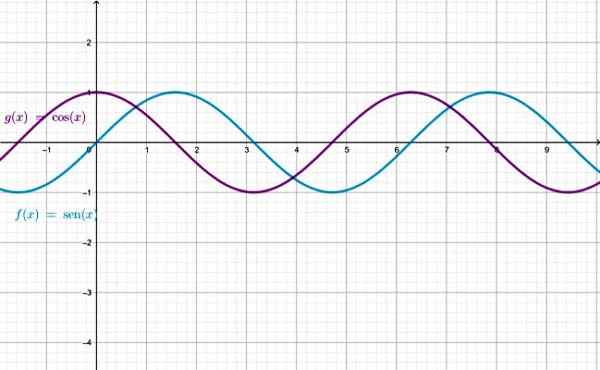 Graf över funktionerna Sen X och Cos X, Observera att de är identiska, förutom att den ena är fördrivna med avseende på den andra. Källa: f. Zapata genom geogebra.
Graf över funktionerna Sen X och Cos X, Observera att de är identiska, förutom att den ena är fördrivna med avseende på den andra. Källa: f. Zapata genom geogebra. Behärskningen av Sen X- och Cos X -funktioner är uppsättningen av verkliga siffror. För de återstående funktionerna finns x -värden för vilka funktionen inte definieras:
-Tg x -funktionen finns inte när x = ± π /2, ± 5π /2 ... detta är alla udda multiplar av π /2.
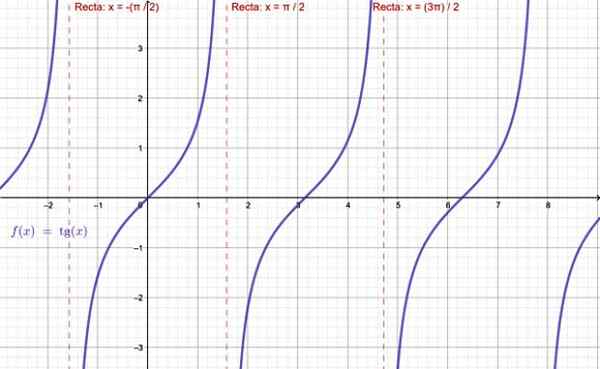 Grafering av tangentfunktionen. Källa: f. Zapata genom geogebra.
Grafering av tangentfunktionen. Källa: f. Zapata genom geogebra. -När det gäller f (x) = cotg x, är denna funktion inte definierad för hela multiplarna av π: ± π, ± 2π, ± 3π ..
Kan tjäna dig: Law of Signs-Y = sec x -funktionen är inte giltig när cos x = 0, vilket utesluter x = ± π /2, ± 5π /2 ... av dess domän.
-Slutligen, för f (x) = skada x, tillhör inte hela multiplarna av π deras domän.
Yo.2.d) Hyperboliska funktioner
Hyperboliska funktioner är speciella kombinationer av exponentiella ochx och e-x Och de kallas som en bröst, koseno .. .hyperbolisk. Liksom med trigonometriska funktioner, även kallad "cirkulär", finns det 6 hyperboliska funktioner:
-Hyperbolisk sinus Senh x:
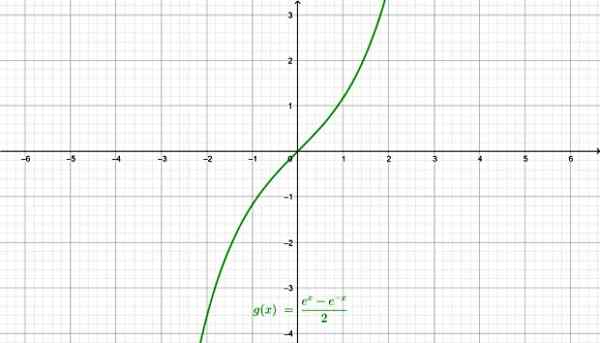 Den hyperboliska sinusfunktionen. Källa: f. Zapata genom geogebra.
Den hyperboliska sinusfunktionen. Källa: f. Zapata genom geogebra. -Hyperbolisk kosinus Kosh x:



-Hyperbolisk cotangent Coth x:
En flexibel kabel, tillverkad av enhetligt och hängande material mellan två punkter, tar formen på en kurva som heter kedja, vilket uttrycks som en hyperbolisk kosinus:
Yo.2.e) omvända trigonometriska funktioner
De motsvarar det omvända av trigonometriska funktioner. Till exempel, vad skulle vara vinkeln (bågen) vars bröst är värd 0.5?
Svaret är arc sen 0.5, som lyder ”bågen sinus på 0.5 ”, och denna vinkel är 30º, även om det i princip inte skulle vara den enda vinkeln vars bröst är värd 0.5, eftersom sen x -funktionen är periodisk. Vad som händer är att om SEN X -funktionen tas i hela dess domän, skulle den inte ha omvänd, så arcoseno -funktionen kunde inte definieras. Frågan avgörs genom att begränsa allt till vinklarna mellan -π/2 och +π/2.
Detta kan uttryckas enligt följande:
Om bågen sen x = θ, betyder det att sin θ = x
Med -π/2 ≤ θ ≤ π/2.
En annan notation som används för arc sen x är f (x) = synd-1 x. Grafen visas nedan:
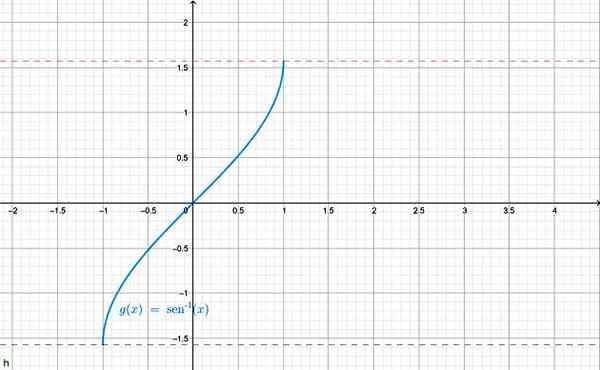 Arcsen X Function Graphics. Källa: f. Zapata genom geogebra.
Arcsen X Function Graphics. Källa: f. Zapata genom geogebra. Det är också möjligt att definiera omvänt för de andra trigonometriska funktionerna, till exempel: Arc cos x = θ och därmed. För var och en är rankningen ordentligt begränsad, för att vara det omvända av motsvarande trigonometriska funktion.
Ii) fungerar enligt dess symmetri
Ii.1) par
Om för allt x som tillhör domänen för f (x) är det uppfyllt att:
f (x) = f (-x)
Det sägs att funktionen är jämn, som de som följer:
- f (x) = x2 - 3
- g (x) = cos x
 Exempel på en parfunktion. Källa: f. Zapata genom geogebra.
Exempel på en parfunktion. Källa: f. Zapata genom geogebra.
Till exempel gör x = 1 i f (x) = x2 - 3 erhålles:
f (1) = 12 - 3 = -2.
Och om x = -1, då:
f (-1) = (-1)2 - 3 = -2.
Båda resultaten är identiska.
De jämna funktionerna har symmetri runt den vertikala axeln, vilket kan ses i föregående figur.
Ii.2) udda funktion
Å andra sidan, ja:
f (-x) = -f (x)
Funktionen är udda.
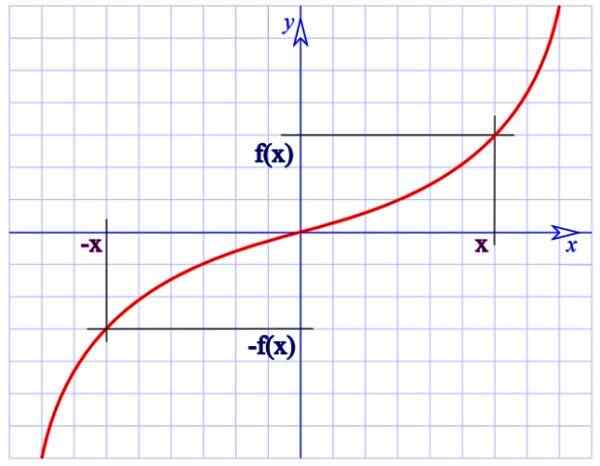 En udda funktion. Källa: Wikimedia Commons.
En udda funktion. Källa: Wikimedia Commons. Till exempel är funktionen f (x) = 1/x för den övre figuren udda, eftersom:
f (-x) = -1/x
OCH
-f (x) = -1/x
En annan viktig imparfunktion är f (x) = sin x.
Observera att udda funktioner har 180 ° rotationssymmetri runt ursprunget (grafen ändras inte om varje punkt på den är 180 ° med avseende på koordinaternas ursprung).
Iii) funktion enligt uttrycket av variabeln
Iii.1) Explicit funktioner
De uttrycks direkt i termer av den beroende variabeln såsom y = f (x). Till exempel:
- f (x) = x3
Iii.2) Implicita funktioner
I implicita funktioner verkar ingen av variablerna tydliga. De uttrycks som f (x, y) = 0, till exempel:
- x2 + och2 -3xy = 0
- xy = - x2+ X-5
De funktioner som beskrivs i hela denna artikel är uttryckliga funktioner.
Iv) Funktioner enligt din grafik
Enligt deras graf kan funktionerna vara kontinuerliga eller diskontinuerliga. Kontinuerliga funktioner kan spåras utan att avbryta slaget, å andra sidan, diskontinuerliga funktioner presenterar hopp. I följande bild är funktionen diskontinuerlig vid x = a:
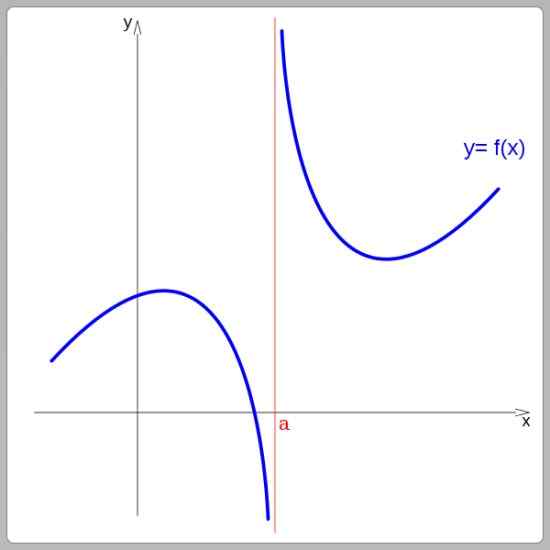 Diskontinuitetsfunktion vid x = a. Källa: Wikimedia Commons.
Diskontinuitetsfunktion vid x = a. Källa: Wikimedia Commons. Exempel på kontinuerliga funktioner är linjär funktion, kvadratisk funktion och sinus- och kosinusfunktioner. Och bland diskontinuerliga funktioner är den förskjutna funktionen och tangentfunktionen.
V) fungerar enligt förhållandet mellan elementen i domänen och intervallet
V.1) injektionsfunktion
En funktion är Injicering När det inte finns två olika element i start- eller domänuppsättningen, som har samma bild i ankomstuppsättningen.
Anta att verkliga funktioner har, om inte annat anges, till exempel:
f (x) = 5x -2
Allt x -värde som tillhör domänen för f (x), som är uppsättningen ℛ för de verkliga siffrorna, har en unik, även verklig bild. Å andra sidan, i denna andra funktion:
g (x) = x2
Det finns olika element i domänen som har samma bild, till exempel x1= 2 och x2= -2:
G (2) = g (-2) = 4.
Sättet att identifiera en injektionsfunktion från dess graf är att dra en horisontell linje, om den skärs till kurvan på mer än en punkt är funktionen icke -injektiv.
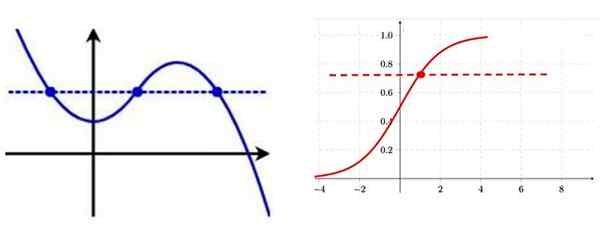 Till vänster en ojämn funktion, notera att det finns flera punkter i grafen med samma vertikala koordinat. Till höger har en injektiv funktion, vid var och en av kurvpunkterna har den en viss "y" -koordinat. Källa: f. Zapata.
Till vänster en ojämn funktion, notera att det finns flera punkter i grafen med samma vertikala koordinat. Till höger har en injektiv funktion, vid var och en av kurvpunkterna har den en viss "y" -koordinat. Källa: f. Zapata. V.2) överjektivfunktion
I onjektivfunktioner, Alla element i ankomstuppsättningen är en bild av något element i startuppsättningen. Ett exempel på överjektivfunktion är samma f (x) = 5x -2, men g (x) = x2 Det är inte, eftersom de tagna värdena g (x) bara är de positiva riktiga och 0.
Domänen kan emellertid omdefinieras så att G (x) var överjektiv, om det till exempel ändras till alla positiva riktiga plus 0.
V.3) Biojektionsfunktion
Slutligen kallas en funktion som är både injektiv och överjektiv, Bijektiv-. Exempel på bijektivfunktioner är: den relaterade funktionen, den exponentiella funktionen och logaritmfunktionen.
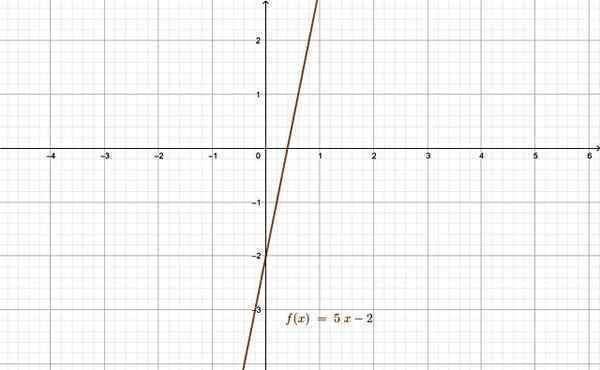 Den relaterade funktionen är ett bra exempel på bijjektivfunktion. Källa: f. Zapata genom geogebra.
Den relaterade funktionen är ett bra exempel på bijjektivfunktion. Källa: f. Zapata genom geogebra. Referenser
- E-math zon. Typer av funktioner. Återhämtat sig från: Emathzone.com.
- Hoffman, J.G. Urval av matematikfrågor. Ed. Spphinx.
- Matematik är kul. Commons Functions Reference. Återhämtat sig från: Mathisfun.com.
- Requena, b. Universumsformler. Typer av funktioner. Återhämtat sig från: universalformulor.com.
- Stewart, J. 2006. Preccculment: Matematik för beräkning. Femte. Utgåva. Cengage Learning.
- « Ititrio struktur, egenskaper, användningar, erhållning
- Iterbio struktur, egenskaper, användningar, erhållning »


=\frac1x)
=\frac4x-3x-1)
=\frac2-x^2x^2-x-1)
=\fraccx)
)
=\sqrtx-3)
=\sqrt[3]2x^5-7)



=a\cdot&space;cosh\left&space;(\fracxa&space;\right&space;))
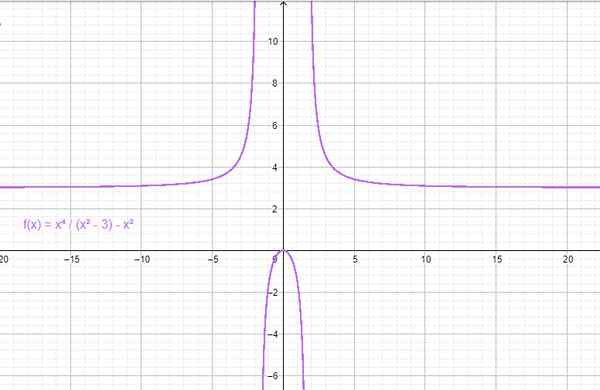
=\fracx^4x^2-3-x^2)