Oblicual Parabolic Shot Egenskaper, formler, ekvationer, exempel

han Oblicual parabolic shot Det är ett särskilt fall av den fria fallrörelsen där projektilens initiala hastighet bildar en viss vinkel med horisontellt, vilket resulterar i en parabolisk väg.

Det fria fallet är ett fall av rörelse med konstant acceleration, där acceleration är tyngdkraften, som alltid pekar vertikalt ner och har en storlek på 9,8 m/s^2. Det beror inte på degen av projektilen, som Galileo Galilei demonstrerade 1604.

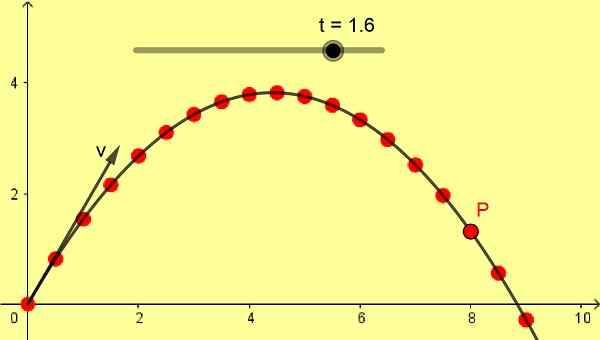
Figur 1. Oblicual parabolic shot. (Egen utarbetande)

Om den initiala projektilhastigheten är vertikal, har det fria fallet en rak och vertikal bana, men om den initiala hastigheten då är sned med banan för fritt fall är en parabolisk kurva, också demonstrerad av Galileo.

Exempel på parabolisk rörelse är banan som följer en baseball, kulan som skjuts av en kanon och vattenstrålen som kommer ut ur en slang.

Figur 1 visar ett sned paraboliskt skott på 10 m/s med en vinkel på 60º. Skalan är i meter och de successiva P -positionerna tas med en skillnad på 0,1 s från det första ögonblicket 0 sekunder.

[TOC]

Formler

Rörelsen av en partikel beskrivs fullständigt om dess position är känd, dess hastighet och dess acceleration som en funktion av tiden.

Den paraboliska rörelsen till följd av ett snett skott är superpositionen av en horisontell rörelse med konstant hastighet, plus en vertikal rörelse med konstant acceleration lika med accelerationen av tyngdkraften.

Formlerna som gäller för det sneda paraboliska skottet är det som motsvarar en rörelse med konstant acceleration a = g, Observera att Bold har använts för att indikera att acceleration är en vektorbelopp.

Kan tjäna dig: naturliga satelliter

Position och hastighet 

I en konstant accelerationsrörelse beror positionen matematiskt på tiden på ett kvadratiskt sätt.

Om vi ​​betecknar r(T) Positionen till tiden t, rantingen Den ursprungliga omedelbara positionen, vantingen Den första hastigheten, g acceleration och t = 0 Som det första ögonblicket formeln som ger positionen för varje ögonblick t är:

r(t) = r_antingen + v_antingen T + ½ g t²

Fet i det föregående uttrycket indikerar att det är en vektorekvation.

Hastigheten som en funktion av tiden erhålls från att ta derivatet med avseende på t i positionen och resultatet är:

v(t) = v_antingen + g t

Och för att få acceleration som en funktion av tiden, hastigheten härledd från t resulterande:

till(t) = g

När tiden inte är tillgänglig finns det en relation mellan hastighet och position, som ges av:

v² = vantingen² - 2 g (och - jag)

Ekvationer

Därefter hittar vi ekvationerna som gäller för ett snett paraboliskt skott i kartesisk form.

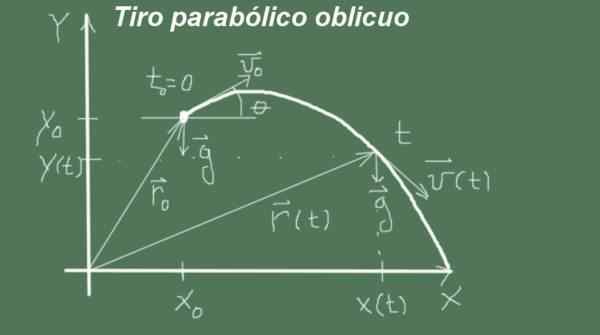
figur 2. Variabler och parametrar för det sneda paraboliska skottet. (Egen utarbetande)

Rörelsen börjar just nu t = 0 Med första position (Xo, jag) och storlekshastighet vantingen och vinkel θ, det vill säga att den initiala hastighetsvektorn är (vantingen cosθ, vantingen senθ). Rörelsen passerar med acceleration 

g = (0, -g).

Parametriska ekvationer

Om vektorformeln som ger positionen som en funktion av tiden tillämpas och komponenter grupperas och utjämnas, kommer ekvationerna som ges av koordinaterna för positionen till när som helst Tid t att erhållas.

x (t) = x_antingen + v_oxe t 

och (t) = y_antingen + v_Oy t -½ g t²

På liknande sätt har ekvationerna för hastighetskomponenter som en tidsfunktion.

Det kan tjäna dig: Normal ansträngning: vad den består av, hur det beräknas, exempel

v_x(t) = v_oxe

v_och(t) = v_Oy - g t 

Var: v_oxe = vantingen cosθ; v_Oy = vantingen Senθ

Banaekvation

y = a x^2 + b x + c

A = -g/(2 Voxe^2)

B = (vOy/voxe + g xantingen/voxe^2)

C = (ochantingen - vOy xantingen / voxe)

Exempel 

Exempel 1

Svara på följande frågor:

a) Varför i paraboliska skjutproblem föraktar vanligtvis effekten av friktion med luft?

b) gör formen på objektet i det paraboliska skottet?

Svar

a) För att en projektil rörelse ska vara parabolisk är det viktigt att luftfriktionskraften är mycket lägre än vikten på objektet som lanseras. 

Om en korkboll eller något lätt material kastas, är friktionskraften jämförbar med vikten och dess bana kan inte närma sig en parabola.

Tvärtom, om det är ett tungt föremål som en sten, är friktionskraften försumbar jämfört med stenens vikt och dess bana gör nära en parabola.

b) formen på objektet som lanseras är också relevant. Om en plata av plan i form av en avionncito lanseras, kommer dess rörelse inte att vara fri eller parabolisk, eftersom formen gynnar luftmotstånd.

Å andra sidan, om samma pappersark är kompakt i form av en boll, är den resulterande rörelsen mycket lik en parabola.

Exempel 2

En projektil lanseras från det horisontella golvet snabbt på 10 m/s och 60º vinkel. Dessa är samma data som figur 1 utvecklades. Med dessa data hittar jag:

a) ögonblick där det når den maximala höjden.

Kan tjäna dig: Vilka är de termiska egenskaperna och vad är det? (Med exempel)

b) den maximala höjden.

c) hastigheten vid maximal höjd.

d) positionen och hastigheten vid 1,6 s.

e) Det ögonblick han spelar jord igen.

f) horisontellt räckvidd.

Lösning till)

Den vertikala hastigheten beroende på tid är

v_och(t) = v_Oy - G t = v_antingen Senθ - g t = 10 Sen60º - 9.8 t = 8.66 - 9.8 t 

Vid den tidpunkten nås den maximala höjden den vertikala hastigheten noll för ett ögonblick.   

8.66 - 9.8 t = 0 ⇒ t = 0.88 s.

Lösning B)

Den maximala höjden ges av koordinaten och För det ögonblick då den höjden nås:

och (0.88S) = Yo jag kommer att t -½ g t^2 = 0 + 8.66*0.88-½ 9.8 0.88^2 = 

3.83 m

Därför är den maximala höjden 3.83 m.

Lösning C)

Hastigheten vid maximal höjd är horisontell:

v_x(t) = v_oxe = v_antingen cosθ = 10 cos60º = 5 m/s 

D) lösning

Positionen vid 1.6 s är:

X (1.6) = 5*1,6 = 8,0 m

och (1.6) = 8.66*1.6-½ 9.8 1.62 = 1.31 m

Lösning E)

När koordinaten berör och den avbryts, då:

och (t) = 8.66*T -½ 9.8 t2 = 0 ⇒ t = 1,77 s

Lösning f)

Det horisontella omfånget är X -koordinaten just nu som spelar jord:

X (1.77) = 5*1,77 = 8,85 m

Exempel 3

Hitta bane -ekvationen med exempel 2 data.

Lösning 

Den parametriska ekvationen för banan är:

x (t) = 5*T

och (t) = 8.66*T -½ 9.8 t^2

Och den kartesiska ekvationen erhålls genom att rensa t av den första och ersätta i den andra

y = 8.66*(x/5) -½ 9.8 (x/5)^2

Förenklande:

y = 1,73 x - 0,20 x^2 

Referenser

1. P. P. Teodorescu (2007). "Kinematik". Mekaniska system, klassiska modeller: partikelmekanik. Kandare.
2. Resnick, Halliday & Krane (2002). Fysikvolym 1. CECSA, Mexiko.
3. Thomas Wallace Wright (1896). Element av mekanik inklusive kinematik, kinetik och statistik. E och fn spon.
4. Wikipedia. Parabolrörelse. Återhämtad från ES.Wikipedia.org.
5. Wikipedia. Kaströrelse.Hämtas från.Wikipedia.org.