Fourier diskret omvandlade egenskaper, applikationer, exempel

De Fourier diskret omvandlad Det är en numerisk metod som används för att definiera prover relaterade till de spektrala frekvenserna som utgör en signal. Studerar periodiska funktioner i stängda parametrar och kastar som ett resultat av en annan diskret signal.

För att få den diskreta omvandlingen av Furier från N -punkter, på en diskret signal, måste följande två villkor på en sekvens uppfyllas X [n]

 x [n] = 0   N n - 1

Genom att uppfylla dessa villkor kan Fouriers diskreta transform definieras som

Tdf

Fourier's Discreet Transform kan definieras som ett provtagning vid N -punkter i Fourier -transformen.

[TOC]

Tolkning av Fouriers diskret transform

Källa: Pexels

Det finns två synpunkter från vilka resultaten som erhålls på en sekvens X kan tolkas_s[n] genom Fouriers diskreta transform.

-Den första motsvarar de spektrala koefficienterna, som redan är kända för Fourier -serien. Det observeras i diskreta periodiska signaler, med prover som sammanfaller med sekvens X_s[N].

-Den andra handlar om spektrumet av en diskret aperiadisk signal, med prover som motsvarar sekvens X_s[N].

Den diskreta omvandlingen är en metod för spektrumet för den ursprungliga analoga signalen. Dess fas beror på provtagningsmoment, medan dess storlek beror på provtagningsintervallet.

Egenskaper

De algebraiska grunden för strukturen utgör den logiska grunden för följande avsnitt.

Linearitet

C . S_n → C . F [S_k]; Om en sekvens multipliceras med en skalar kommer dess transformation också att vara.

T_n + V_n = F [t_k]+F [v_k]; Transformationen av en summa är lika med summan av de transformerade.

Dualitet

F [s_n] → (1/n) s_-K; Om den diskreta omvandlingen av Fourier återkallas till ett uttryck som redan transformerats erhålls samma uttryck, klättring i N inverterad med avseende på den vertikala axeln.

Veck

Jagar liknande mål som i Laplace -omvandlingen, funktionerna för funktionerna hänvisar till produkten bland dess Fourier -transformationer. Upplösningen gäller också för diskreta tider och ansvarar för många moderna procedurer.

X_n * R_n → F [x_n] .F [r_n]; Transformationen av en upplösning är lika med produkten från de transformerade.

X_n . R_n→ F [x_n] * F [r_n]; Transformationen av en produkt är lika med de transformerade upplösningen.

Förflyttning

X_N-m → F [x_k] e ^{-I (2π/n) km} ; Om en följd är försenad i M -prover kommer dess effekt på den diskreta transformationen att vara en modifiering av vinkeln som definieras av (2π/n) km.

Kan tjäna dig: Varför är algebra viktigt i vissa dagliga livssituationer?

Symmetri konjugerad

X_t [-K] = x*_t[k] = x_t [N - K]

Modulation

W^-nm_N . x [n] ↔ x_t[K - m]

Produkt

x [n] y [n] ↔ (1/n) x_t[K]*och_t[K]

Symmetri

X [-n] ↔ x_t[-K] = x*_t[K]

Konjugera

x*[n] ↔ x*_t[-K]

Parsvalekvation 

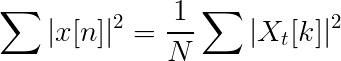
Likheter och skillnader med Fourier -transformen

När det gäller den konventionella transformalen av Fourier har den flera likheter och skillnader. Fouriers transform omvandlar en sekvens till en kontinuerlig linje. På detta sätt sägs det att resultatet av Fourier -variabeln är en komplex verklig variabel funktion.

Fouriers diskreta transform, till skillnad från, får en diskret signal och förvandlar den till ett annat diskret tecken, det vill säga en sekvens.

Vad är användningen av Fouriers diskreta transform?

De tjänar främst till betydande ekvationer, samtidigt som de förvandlar uttryck som härrör till kraftelement. Betecknar differentiella uttryck i former av integrerbara polynomer.

I optimering, modulering och modellering av resultat fungerar det som ett standardiserat uttryck, och är en frekvent resurs för teknik efter flera generationer.

Källa: Pixabay

Historia

Detta matematiska koncept presenterades av Joseph B. Fourier 1811, medan han utvecklade ett fördrag angående Värmespridning. Det antogs snabbt av olika grenar av vetenskap och teknik.

Det upprättades som det huvudsakliga arbetsverktyget i studien av ekvationer med partiella derivat, jämför även med arbetsförhållandet mellan Laplace transformerade och vanliga differentiella ekvationer.

Varje funktion som kan bearbetas med Fourier Transform måste presentera NULLITY utanför en definierad parameter.

Fourier diskret omvandlas och dess omvända

Den diskreta transformen erhålls genom uttrycket:

Efter en diskret sekvens x [n]

Den inversa av Fouriers diskret transform definieras genom uttrycket:

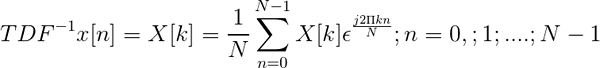Omvänd TDF

Det tillåter när den diskreta transformerade, definiera sekvensen i tidsdomänen X [n].

Stass

Parametreringsprocessen som motsvarar Fouriers diskreta omvandling ligger i ungen. För att arbeta om omvandlingen måste vi begränsa sekvensen i tid. I många fall har signalerna i fråga inte dessa begränsningar.

En följd som inte uppfyller storlekskriterierna som ska tillämpas på den diskreta omvandlingen kan multipliceras med en "fönster" v [n] -funktion, vilket definierar beteendet hos successionen i en kontrollerad parameter.

Kan tjäna dig: Cirkulära permutationer: Demonstration, exempel, Löst övningar

X [n] . V [n]

Spektrumbredden beror på fönsterbredden. När fönsterbredden ökar kommer den beräknade transformerade att vara smalare.

Ansökningar

Beräkning av den grundläggande lösningen

Fouriers Discreet Transform är ett kraftfullt verktyg i studien av diskreta successioner.

Fourier's Discreet Transform Transforms en kontinuerlig variabel funktion, till en diskret variabel transform.

Cauchys problem för värmeekvation utgör ett ofta tillämpningsfält av Fouriers diskreta transform. Där funktionen genereras Dirichlet värme eller kärnkärna, som gäller för värderingsprovtagning i en definierad parameter.

Signalteori

Det allmänna skälet till tillämpningen av Fouriers diskreta omvandling i denna gren beror mest på den karakteristiska nedbrytningen av en signal som en oändlig överlappning av lättare behandlingsbara signaler.

Det kan vara en ljudvåg eller en elektromagnetisk våg, Fouriers diskreta transform uttrycker den i en enkel vågöverlappning. Denna representation är ganska ofta inom elektroteknik.

Fouriers serie

De är definierade serier när det gäller kosenos och bröst. De tjänar till att underlätta arbetet med allmänna periodiska funktioner. När de tillämpas är de en del av upplösningsteknikerna för partiella och vanliga differentiella ekvationer.

Fourier -serien är ännu mer allmänna än Taylors serie, eftersom de utvecklar periodiska diskontinua -funktioner som inte har någon representation i Taylor -serien.

Andra former av Fourier -serien

Att analytiskt förstå Fouriers omvandling är det viktigt.

-Fourier -serien på en 2L -periodfunktion:

Många gånger är det nödvändigt att anpassa strukturen i en Fourier-serie, till periodiska funktioner vars period är p = 2l> 0 i intervallet [-l, l].

-Fourier -serien i jämna och udda funktioner

Intervallet [-π, π] beaktas som erbjuder fördelar när man utnyttjar de symmetriska egenskaperna hos funktionerna.

Kan tjäna dig: Finite Set: Egenskaper, exempel, lösta övningar

Om f är vridmoment är Fourier -serien etablerad som en serie kosenos.

Om F är udda, är Fourier -serien etablerad som en serie bröst.

-Komplex notering av Fourier -serien

Om du har en f (t) -funktion, som uppfyller alla krav i Fourier-serien, är det möjligt att beteckna den i intervallet [-t, t] med sin komplexa notation: 

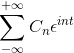
Exempel

När det gäller beräkningen av den grundläggande lösningen presenteras följande exempel:

Laplace -ekvation

Värmeekvation

Schrödinger -ekvation

Vågekvation

Å andra sidan finns det exempel på tillämpning av Fouriers diskreta omvandling inom signalteori:

-Systemidentifieringsproblem. Etablerad f och g

-Problem med konsistensen av utsignalen

-Problem med signalfiltreringen

Övningar

Övning 1

Beräkna Fouriers diskret transformation för följande följd.

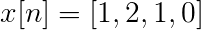
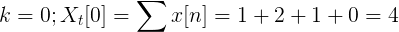
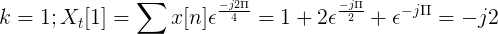
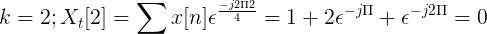
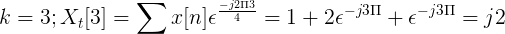
X [n] tdf kan definieras som:

X_t[k] = 4, -j2, 0, j2 för k = 0, 1, 2, 3

Övning 2

Det är ville bestämma genom en digital algoritm den spektrala signalen som definieras av uttrycket x (t) = e^-t. Där den maximala frekvens begärande koefficienten är f_m= 1Hz. En harmonisk motsvarar F = 0.3 Hz. Felet är begränsat till mindre än 5%. Beräkna F_s , D och n.

Med hänsyn till provtagningsteoremet F_s = 2f_m = 2 Hz

En frekvensupplösning av F₀ = 0.1 Hz, där d = 1/0,1 = 10s erhålls

0.3 Hz är frekvensen som motsvarar index k = 3, där n = 3 × 8 = 24 provtagning. Indikerar att F_s = N/d = 24/10 = 2.4> 2

Eftersom syftet är att uppnå minst möjliga värde för n kan följande värden betraktas som en lösning:

F₀ = 0.3 Hz

D = 1/0.3 = 3.33s

K = 1

N = 1 × 8 = 8

Referenser

1. Behärskning av den diskreta Fourier -omvandlingen i en, två eller flera dimensioner: fallgropar och artefakter. Isaac amidor. Springer Science & Business Media, 19 juli. 2013
2. DFT: En ägarhandbok för den diskreta Fourier -transformen. William L. Briggs, Van Emden Henson. Siam, 1 jan. nittonhundranittiofem
3. Digital signalbehandling: teori och praktik. D. Sundararajan. World Scientific, 2003
4. Transformer och snabba algoritmer för signalanalys och representationer. Guoan BI, Yonghong Zeng. Springer Science & Business Media, 6 dec. 2012
5. Diskreta och kontinuerliga Fourier -transformationer: analys, applikationer och snabba algoritmer. Eleanor Chu. CRC Press, 19. 2008