Hemsida
Matematik
Rektangel trapesegenskaper, relationer och formler, exempel

Matematik

Rektangel trapesegenskaper, relationer och formler, exempel

3543
580
Lars Eriksson

En rektangel trapes Det är en platt figur på fyra sidor, så att två av dem är parallella med varandra, kallade baser Och även en av de andra sidorna är vinkelrätt mot baserna.

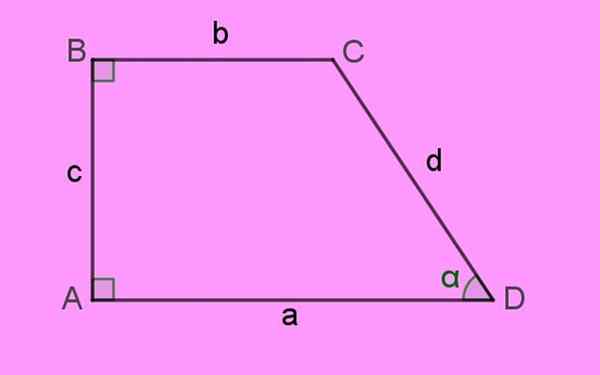
Av denna anledning är två av de inre vinklarna raka, det vill säga de mäter 90º. Därför namnet på "rektangel" som ges till figuren. Följande bild av en rektangel trapeze klargör dessa egenskaper:

[TOC]

Trapeselement

Elementen i trapezoiden är:

-Baser

-Häckar

-Höjd

-Inre vinklar

-Genomsnittlig bas

-Diagonaler

Vi kommer att beskriva dessa element med hjälp av figurerna 1 och 2:

Figur 1. En rektangel trapes, kännetecknad av att ha två inre vinklar på 90º: A och B. Källa: f. Zapata.

Sidorna på rektangeln trapezoid betecknas med små bokstäver A, B, C och D. Hörnen på figuren eller Häckar De anges i stora bokstäver. Till sist Inre vinklar De uttrycks med grekiska brev.

Enligt definitionen baser Av denna trapezoid är sidor A och B, som som observerats är parallella och också har olika längd.

Den vinkelräta sidan till båda baserna är sidan c till vänster, vilket är höjd h av trapes. Och slutligen finns det sida D, som bildar den akuta vinkeln a med sidan a.

Summan av Inre vinklar av en fyrkant är 360º. Det uppskattas lätt att den saknade vinkeln C i figuren är 180 - α.

De genomsnittlig bas Det är segmentet som ansluter sig till mitten av icke -parallella sidor (EF -segmentet i figur 2).

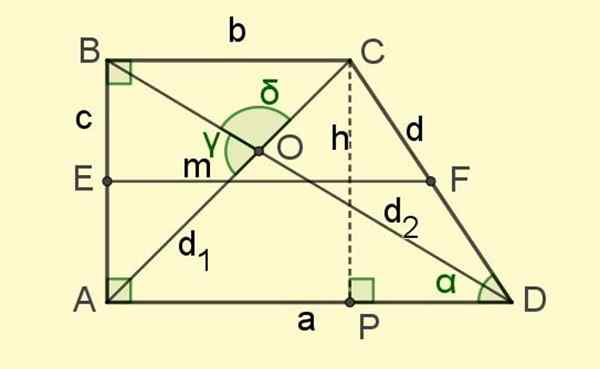figur 2. Elementen i rektangeln trapezoid. Källa: f. Zapata.

Och slutligen finns det diagonalerna D₁ och D₂, Segmenten som förenar de motsatta vertikalerna och som korsar vid punkt O (se figur 2).

Relationer och formler

Höjd h av trapezoiden

H = c

Omkrets P

Det är måtten på konturen och beräknas genom att lägga till sidorna:

Omkrets = a + b + c + d

Sidan d Det uttrycks i termer av höjd eller sida c Genom Pythagoras teorem:

D = √ (a-b)² + c²

Byte i omkretsen:

P = A + B + C + √ (A-B)² + c²

Genomsnittlig bas

Det är basens halvkroppar:

Medium bas = (a+b)/2

Ibland hittas den genomsnittliga basen som uttrycks på detta sätt:

Medium bas = (större bas + mindre bas) /2

Område

Område A av trapes är produkten från den genomsnittliga basen efter höjd:

A = (Större bas + mindre bas) x höjd /2

A = (a+b) c/2

Diagonaler, sidor och vinklar

Flera trianglar visas i figur 2, både rektanglar och icke -rektanglar. För de som har rätt trianglar kan de appliceras av Pythagoras teorem och de som inte gör det, kosinusens och bröstets teorier.

Kan tjäna dig: transcendenta nummer: vad är, formler, exempel, övningar

På detta sätt finns det förhållanden mellan sidorna och mellan sidorna och trapezios inre vinklar.

CPA -triangel

Det är rektangel, benen är desamma och de är värda B, medan hypotenusen är diagonalen D₁, därför:

d₁² = B² + b² = 2b²

Triangel

Det är också rektangel, benen är till och c (eller också till och h) Och hypotenusen är d₂, så att:

d₂² = a² + c²= a² + h²

CDA -triangel

Eftersom denna triangel inte är rektangel appliceras kosinussteoremet, eller även bröstet.

Enligt Coseno Theorem:

d₁² = a² + d² - 2ad cos a

CDP -triangel

Denna triangel är rektangel och med sina sidor byggs de trigonometriska orsakerna till vinkeln a:

sin α = h/d

cos α = pd/d

Men PD = A - B -sidan, därför:

cos a = (a -b) / d → a - b = d cos a

a = b + d cos a

Du har också:

Tg α = sin a / cos α = H / (a-b) → H = Tg a (a-b)

CDB -triangel

I denna triangel har vi vinkeln vars toppunkt är i C. Det är inte markerat i figuren, men i början stod det ut att det är värt 180 - a. Denna triangel är inte rektangel, så kosinus teorem eller bröstteorem kan tillämpas.

Nu kan det lätt demonstreras att:

Sen (180 - α) = sin α

cos (180 - α) = - cos a

Tillämpa Coseno Theorem:

d₂² = D² + b²- 2dB cos (180 - α) = D² + b²+ 2dB COS a

Exempel på rektanglar

Trapezios och särskilt rektanglarna finns på många sidor, och ibland inte alltid påtagliga. Här har vi flera exempel:

Trapecio som designelement

Geometriska figurer finns i överflöd i arkitekturen för många byggnader, till exempel denna kyrka i New York, som visar en struktur i form av rektangel trapezoid.

Trapezoidal form är också ofta i utformningen av containrar, containrar, blad (Fräs eller exakt), ark och i grafisk design.

Figur 3. Angel inuti en rektangel trapezoid i en kyrka i New York. Källa: David Goehring genom Flickr.

Trapesformad våggenerator

Elektriska signaler kan inte bara vara fyrkantiga, sinus eller triangulära. Det finns också trapesformade signaler som är användbara i många kretsar. I figur 4 finns det en trapezoidal signal som består av två rektanglar. Mellan dem bildar de en enda isosceles trapezoid.

Kan tjäna dig: delare av 8: vad är och enkel förklaring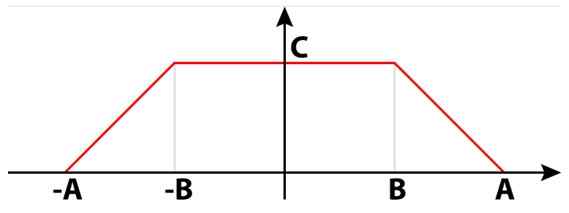

Figur 4. En trapesformad signal. Källa: Wikimedia Commons.

I den numeriska beräkningen

För att numeriskt beräkna den definierade integralen av funktionen f (x) mellan a och b, används trapesregeln för att ungefärliga området under diagrammet för f (x). I följande figur, till vänster de integrerade tillvägagångssätten med en enda rektangel trapezoid.

Ett bättre tillvägagångssätt är den rätta figuren, med flera rektanglar.

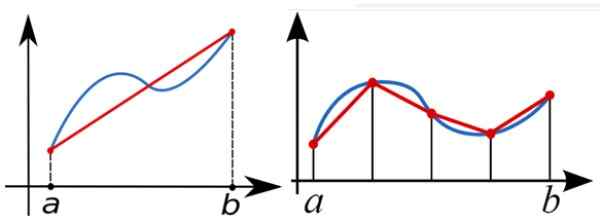Figur 5. En definierad integral mellan A och B är inget annat än området under kurvan F (x) mellan dessa värden. En rektangel trapezoid kan fungera som den första metoden till det området, men ju mer trapesoider används, desto bättre är tillvägagångssättet. Källa: Wikimedia Commons.

Trapesformad belastningsbalk

Krafterna är inte alltid koncentrerade på en enda punkt, eftersom de kroppar som de agerar har märkbara dimensioner. Så är fallet med en bro genom vilken fordon kontinuerligt cirkulerar, vattnet i en pool på de vertikala väggarna på samma eller ett tak på vilket vatten eller snö ackumuleras.

Det är därför krafterna distribueras per enhet längd, yta eller volym, beroende på kroppen som de agerar.

När det gäller en stråle kan en kraft som är distribuerad per längdenhet ha olika distributioner, till exempel den för rektangel trapes som visas nedan:

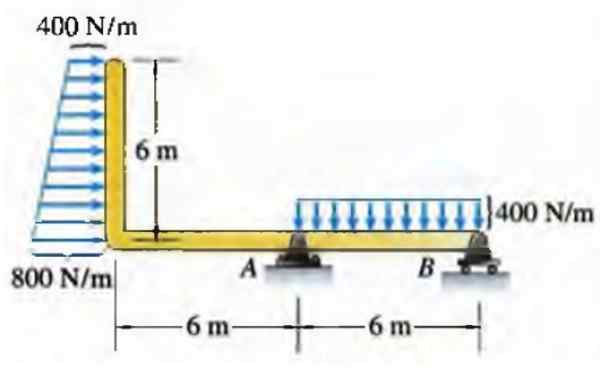Figur 6. Massor på en balk. Källa: Bedford, till. nitton nittiosex. Statisk. Addison Wesley Inter -American.

I verkligheten motsvarar inte alltid distributioner regelbundna geometriska former som denna, men de kan vara ett bra tillvägagångssätt i många fall.

Som utbildnings- och inlärningsverktyg

Block och ark med geometriska former, inklusive trapezoider, är mycket användbara för barn att bekanta sig från en tidig ålder med den fascinerande världen av geometri.

Figur 7. Block med enkla geometriska former. Hur många rektanglar är dolda i blocken? Källa: Wikimedia Commons.

Löst övningar

- Övning 1

I rektangeln trapezoid i figur 1 är den största basen värd 50 cm och den minsta basen är lika med 30 cm, det är också känt att den sneda sidan mäter 35 cm. Hitta:

a) Vinkel a

b) höjd

c) omkrets

d) medelbas

f) diagonal

Lösning till

Uttalandeuppgifterna sammanfattas på detta sätt:

A = högre bas = 50 cm

B = mindre bas = 30 cm

D = lutande sida = 35 cm

Kan tjäna dig: grundläggande operationer

För att hitta vinkeln a besöker vi avsnittet Formler och ekvationer, för att se vilken som bäst passar de data som erbjuds. Den eftertraktade vinkeln finns i flera av de analyserade trianglarna, till exempel CDP.

Där har vi denna formel, som innehåller det okända och även de uppgifter vi känner:

cos α = (a-b) / d

Därför:

α = bågar [(a-b) / d] = bågar [(50-30) / 35] = bågar 20/35 = 55.15 º

Lösning B

Från ekvationen:

sin α = h/d

H = D.synd = 35 sen 55.15 º cm = 28.72 cm

Lösning C

Omkretsen är summan av sidorna, och eftersom höjden är lika med sidan C, måste vi:

C = h = 28.72 cm

Därför:

P = (50 + 30 + 35 + 28.72) cm = 143.72 cm

Lösning D

Den genomsnittliga basen är basens halvkroppar:

Medium bas = (50 + 30 cm)/2 = 40 cm

Lösning E

Trapezoidområdet är:

A = genomsnittlig bas x höjd = 40 cm x 28.72 = 1148.8 cm².

Lösning f

För den diagonala d₁ Denna formel kan användas:

d₁² = B² + b² = 2b²

d₁²= 2 x (30 cm)² = 1800 cm²

d₁ = √1800 cm² = 42.42 cm

Och för den diagonala d₂:

d₂² = D² + b²+ 2dB COS a = (35 cm)² + (30 cm)² + 2 x 35 x 30 cm² Cos 55.15 º = 3325 cm²

d₂ = √ 3325 cm² = 57.66 cm

Detta är inte det enda sättet att hitta D₂, Eftersom det också finns dab -triangeln.

- Övning 2

Följande hastighetsgraf beroende på en mobil som har en enhetligt accelererad rätlinjig rörelse. Beräkna det avstånd som mobilen har kört under tidsintervallet mellan 0.5 och 1.2 sekunder.

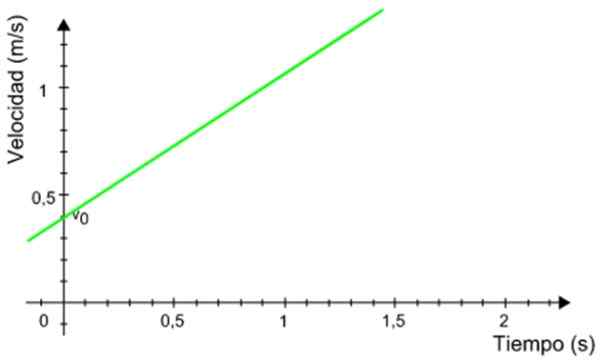Figur 8. Grafik mot tiden för en mobil med enhetligt accelererad Reket -rörelse. Källa: Wikimedia Commons.

Lösning

Avståndet som röret har motsatt sig motsvarande området under diagrammet, avgränsat av det angivna tidsintervallet.

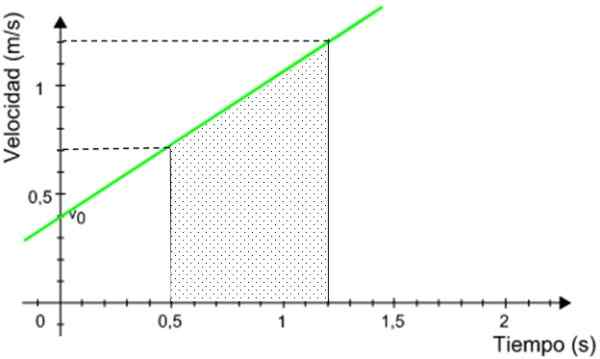Figur 9. Det avstånd som mobilen reste motsvarar området under grafiken. Källa: modifierad av f. Zapata.

Det skuggade området är området för en rektangel trapezoid, som ges av: