Skalen triangel

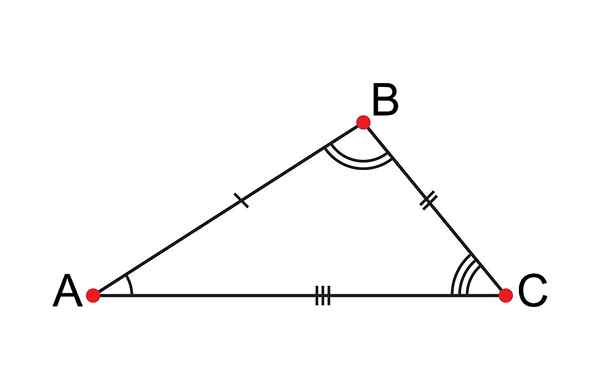
Scalene Triangle har alla sina ojämna sidor

Vad är en skalen triangel?

En skalen triangel Det är en tresidig polygon, där alla har olika åtgärder eller längder; Av den anledningen fick det namnet Escaleno, som på latin betyder ojämlikt.

Trianglarna är polygoner som betraktas som de enklaste i geometri, eftersom tre sidor, tre vinklar och tre vertikaler bildas. När det gäller skalen triangel, för att ha alla olika sidor, innebär det att dess tre vinklar också kommer att vara.

Skala trianglar egenskaper

Skala trianglar är enkla polygoner eftersom ingen av dess sidor eller vinklar har samma mått, till skillnad från isosceles och jämviktstrianglar.

Eftersom alla deras sidor och vinklar har olika mått betraktas dessa trianglar som oregelbundna konvexa polygoner.

Enligt amplituden hos inre vinklar klassificeras skalen trianglar som:

• Skalen rektangel triangel: Alla sidor är olika. En av dess vinklar är rak (90^antingen) och de andra är akuta och med olika åtgärder.
• Triangel: Alla sidor är olika och en av dess vinklar är stöt (> 90^antingen).
• Skalen akutangle triangel: Alla sidor är olika. Alla dess vinklar är akuta (< 90^antingen), Med olika åtgärder.

En annan egenskap hos Scalene Triangles är att på grund av inkonsisten.

Komponenter/element

Median

Det är en linje som lämnar från mittpunkten på ena sidan och når motsatt toppunkt. De tre medierna deltar vid en punkt som heter Baricentro eller Centroid.

Bisektorn

Det är en halv -rätt som delar upp varje vinkel i två vinklar med lika mått. Bisektorerna i en triangel överensstämmer med incitret.

MediTrix

Det är ett segment vinkelrätt mot triangelns sida, som har sitt ursprung i mitten av detta. Det finns tre medier i en triangel och deltar vid en punkt som heter Circumcentro.

Höjden 

Det är linjen som går från toppunktet till motsatt sida, och även denna linje är vinkelrätt mot den sidan. Alla trianglar har tre höjder som sammanfaller vid en punkt som kallas ortotenter.

Egenskaper i Escaleno Triange

Skala trianglar definieras eller identifieras eftersom de har flera egenskaper som representerar dem, härstammar från de teorier som föreslagits av stora matematiker. Dom är:

Inre vinklar

Summan av inre vinklar är alltid lika med 180^antingen.

Sidans summa

Summan av måtten på två sidor bör alltid vara större än måttet på den tredje sidan, a + b> c.

Inkongruösa sidor

Alla sidor av klättringstrianglarna har olika åtgärder eller längder; det vill säga de är inkongruösa.

Inkongruösa vinklar

Eftersom alla sidor av skalen triangeln är olika kommer dess vinklar också att vara. Summan av de inre vinklarna kommer emellertid alltid att vara lika med 180 °, och i vissa fall kan en av dess vinklar vara stöt eller rak, medan i andra kommer alla dess vinklar att vara akuta.

Kan tjäna dig: multiplikativa problem för barn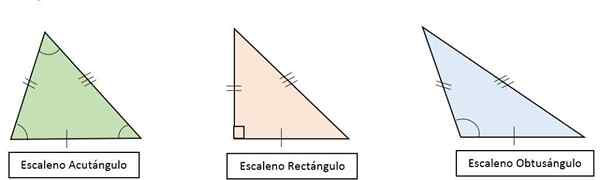 Typer av skalstrianglar enligt deras vinklar

Höjd, median, mediatrix och bisector är inte sammanfallande

Liksom alla triangel har Escaleno olika linjer med linjer som komponerar den, till exempel: Höjd, medium, MediaTrix och Bisector.

På grund av dess sidor kommer ingen av dessa linjer, i denna typ av triangel att sammanfalla i en singel.

Orocentro, Baricentro, Incentro och Circumcentro är inte sammanfallande

Liksom höjden representeras median, bisector och MediaTrix av olika linjesegment, i en skala triangel kommer mötespunkterna -ortocentret, incitenten och circumcentro baricenter -kommer att hittas på olika punkter (det vill säga de inte sammanfaller).

Beroende på om triangeln är akutangel, rektangel eller stöt, har ortocentret olika platser:

till. Om triangeln är akutangel kommer ortocentret att vara inne i triangeln.

b. Om triangeln är rektangel kommer ortocentret att sammanfalla med toppen på rak sida.

c. Om triangeln är stöt kommer ootocentret att vara utanför triangeln.

Relativa höjder

Höjderna är relativt sidorna.

När det gäller skalen triangel kommer dessa höjder att ha olika åtgärder. Varje triangel har tre relativa höjder och för att beräkna dem används Herón -formeln.

Omkretsberäkning, area, höjd och sidor

Hur man beräknar omkretsen?

Omkretsen av en polygon beräknas med sidorna av sidorna.

Liksom i detta fall har Scalaene Triangle alla sidor med en annan mått, kommer dess omkrets att vara:

P = sida till + sida B + sida C.

Hur man beräknar området?

Trianglarna beräknas alltid med samma formel, vilket multiplicerar basen efter höjd och delning med två:

Area = (bas _* H) ÷ 2

I vissa fall är höjden på skalen triangeln inte känd, men det finns en formel som föreslogs av matematikern Herón för att beräkna området och veta måtten på de tre sidorna av en triangel.

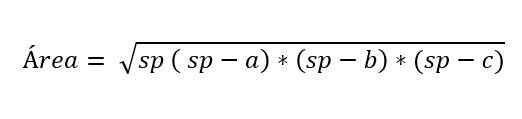
Var:

• A, B och C representerar sidorna på triangeln.
• SP motsvarar triangelns halvperimeter, det vill säga hälften av omkretsen:

sp = (a + b + c) ÷ 2

I händelse av att endast två av sidorna av triangeln och vinkeln som bildas mellan dem kan, kan området beräknas genom att tillämpa de trigonometriska skälen. Således måste du:

Area = (sida _* H) ÷ 2

Där höjd (h) är produkten på ena sidan genom motsatt vinkel. Till exempel kommer området för varje sida att vara:

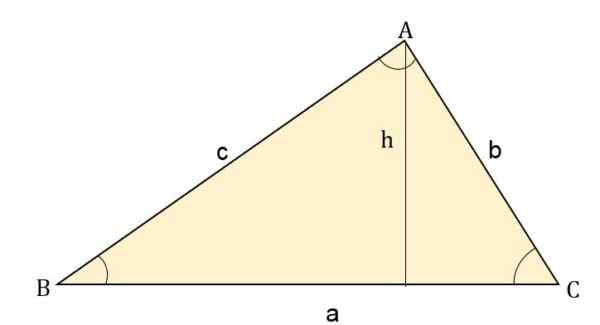
• Area = (b _* c _* sin a) ÷ 2
• Area = (a _* c _* synd b) ÷ 2.
• Area = (a _* b _* Sen c) ÷ 2

Hur man beräknar höjden?

Liksom alla sidor av den skala triangeln de är olika är det inte möjligt att beräkna höjden med Pythagoras teorem.

Från Herón -formeln, som är baserad på måtten på de tre sidorna av en triangel, kan området beräknas.

Kan tjäna dig: Factorial Notation: Concept, Exempel och övningar

Höjden kan vara tydlig från den allmänna formeln för området:

Formel för att beräkna höjden på en skalen triangel

Sidan ersätts av måtten på sidan A, B eller C.

Ett annat sätt att beräkna höjden när värdet på en av vinklarna är kända är att tillämpa de trigonometriska skälen, där höjden kommer att representera en triangel Cateto.

Till exempel, när den motsatta vinkeln är känd för höjd, kommer den att bestämmas av bröstet:

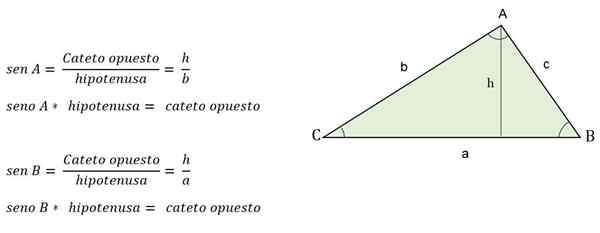Trigonometrisk formel för att beräkna höjden på en skalen triangel

Hur man beräknar sidorna?

När du har måtten på två sidor och vinkeln i motsats till dessa är det möjligt att bestämma den tredje sidan som applicerar Cosenos -teoremet.

Till exempel i en AB -triangel dras höjden relativt AC -segmentet. På detta sätt är triangeln uppdelad i två rektangel trianglar.

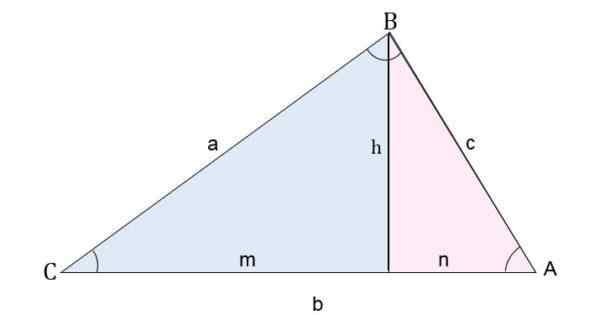Uppdelning av en skalen triangel i två rektanglar för att beräkna sidorna

För att beräkna sida C (segment AB) appliceras Pythagoras teorem för varje triangel:

• För den blå triangeln måste du:

c² = h² + m²

Som m = b - n ersätts det:

c² = h² + b² (B - n)²

c² = h² + b² - 2 miljarder + N².

• För den rosa triangeln måste du:

h² = a² - n²

Det ersätts i föregående ekvation:

c² = a² - n² + b² - 2 miljarder + N²

c² = a² + b² - 2bn.

Att veta att n = a _* COS C, ersätts i föregående ekvation och värdet på sidan C erhålls:

c² = a² + b² - 2B_* till _* cos c.

Enligt lagen om Cosenos kan sidorna beräknas som:

• till² = B² + c² - 2B_* c _* grejer.
• b² = a² + c² - 2: a_* c _* cos b.
• c² = a² + b² - 2B_* till _* cos c.

Det finns fall där måtten på triangelsidorna inte är kända, men dess höjd och vinklar som bildas i vertikalerna. För att bestämma området i dessa fall är det nödvändigt att tillämpa trigonometriska skäl.

Genom att känna till vinkeln på en av dess vertikaler identifieras kategorin och motsvarande trigonometriska orsaker används:

Trigonometrisk formel för att beräkna sidorna på en skalen triangel

Till exempel kommer Cateto AB att vara motsatt för vinkel C, men intill vinkeln a. Beroende på sidan eller benet som motsvarar höjden rensas den andra sidan för att få värdet på detta.

Löst övningar

Första träning

Beräkna området och en höjd av Escalano ABC -triangeln, veta att dess sidor är:

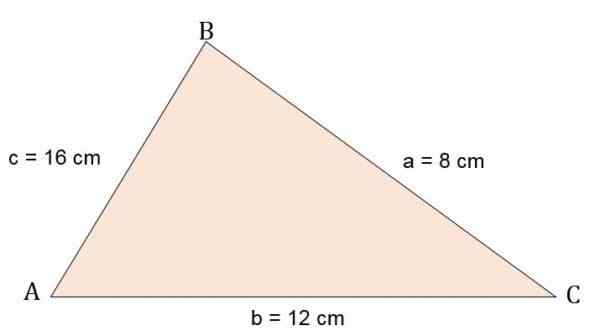
A = 8 cm.

B = 12 cm.

C = 16 cm.

Lösning

Eftersom data ges måtten på de tre sidorna av skalen triangeln.

Eftersom du inte har värdet på höjden kan området bestämmas genom att tillämpa Herón -formeln.

Först beräknas semi -perimeter:

sp = (a + b + c) ÷ 2

sp = (8 cm + 12 cm + 16 cm) ÷ 2

sp = 36 cm ÷ 2

sp = 18 cm.

Nu ersätts värdena i Heróns formel:

Kan tjäna dig: absolut frekvens: formel, beräkning, distribution, exempel Herón -formel

Att veta området kan beräknas den relativa höjden till sida B. Från den allmänna formeln, rensa den har du:

Area = (sida _* H) ÷ 2

46, 47 cm² = (12 cm _* H) ÷ 2

H = (2 _* 46,47 cm²) ÷ 12 cm

H = 92,94 cm² ÷ 12 cm

H = 7,75 cm.

Andra träning

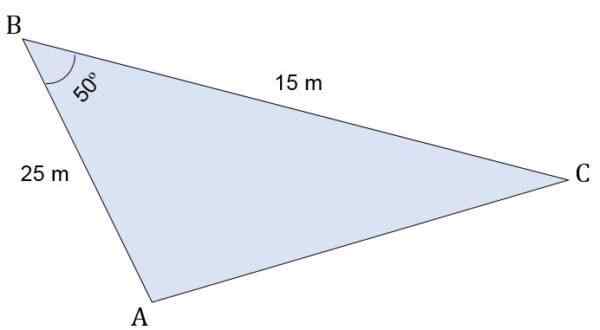
Med tanke på ABC Escalano Triangle, vars åtgärder är:

• Segment AB = 25 m.
• Segment BC = 15 m.

I toppunkt B bildas en vinkel på 50º. Beräkna höjden i förhållande till sidan C, omkretsen och området för den triangeln.

Lösning

I det här fallet finns det två sidor. För att bestämma höjden är det nödvändigt att beräkna måttet på den tredje sidan.

Eftersom den motsatta vinkeln ges till de givna sidorna är det möjligt att tillämpa lagen om Cosenos för att bestämma måtten på AC (B) -sidan:

b² = a² + c² - 2: a_*c _* cos b

Var:

A = bc = 15 m.

C = ab = 25 m.

B = AC.

B = 50^antingen.

Uppgifterna byts ut:

b² = (15)² + (25)² - 2_*(femton)_*(25) _* cos 50

b² = (225) + (625) - (750) _* 0,6427

b² = (225) + (625) - (482,025)

b² = 367.985

B = √367,985

B = 19,18 m.

Eftersom du redan har värdet på de tre sidorna beräknas omkretsen av den triangeln:

P = sida till + sida B + sida C

P = 15 m + 25 m + 19, 18 m

P = 59,18 m

Det är nu möjligt att bestämma området genom att tillämpa Herón -formeln, men först måste semi -perimetern beräknas:

sp = p ÷ 2

sp = 59,18 m ÷ 2

sp = 29,59 m.

Mätningarna på sidorna och halvperimetern i Herón -formeln ersätts:

Slutligen, och känner till området, kan den relativa höjden beräknas till sidan C. Från den allmänna formeln, rensa den måste du:

Area = (sida _* H) ÷ 2

143,63 m² = (25 m _* H) ÷ 2

H = (2 _* 143,63 m²) ÷ 25 m

H = 287,3 m² ÷ 25 m

H = 11,5 m.

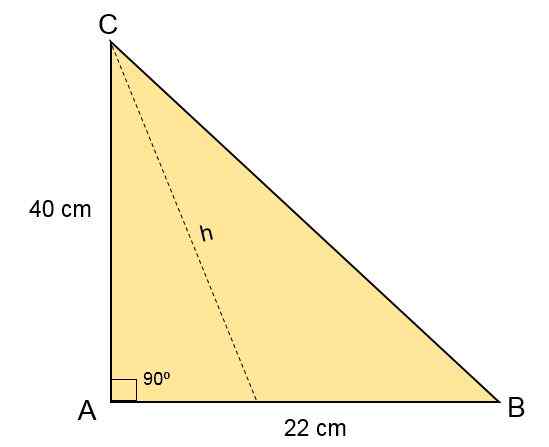
Tredje träning

I Escaleno ABC -triangeln mäter B -sidan 40 cm, C -sidan mäter 22 cm, och i toppen är A en vinkel på 90^antingen. Beräkna området för den triangeln.

Lösning

I detta fall ges måtten på två sidor av ABC -skala triangeln, liksom vinkeln som bildas i toppen till.

För att bestämma området är det inte nödvändigt att beräkna måttet på sidan A, eftersom genom trigonometriska skäl är vinkeln att använda för att hitta den.

Eftersom motsatt vinkel är känd i höjden, bestäms detta av produkten på ena sidan och vinkelns bröst.

Byt ut i den områdesformel du måste:

• Area = (sida _* H) ÷ 2
• H = c _* sin a

Area = (b _* c _* sin a) ÷ 2

Area = (40 cm _* 22 cm _* Sen 90) ÷ 2

Area = (40 cm _* 22 cm _* 1) ÷ 2

Area = 880 cm² ÷ 2

Area = 440 cm².

Referenser

1. Álvaro Rendón, till. R. (2004). Teknisk ritning: Aktivitetsnotbok.
2. Ángel Ruiz, h. B. (2006). Geometrier. Cr teknologisk, .
3. Ängel, a. R. (2007). Elementär algebra. Pearson Education,.
4. Baldor, a. (1941). Algebra. Havanna: Kultur.
5. Barbosa, J. L. (2006). Platt euklidisk geometri. Rio de janeiro,.
6. Coxeter, h. (1971). Geometriens grunder. Mexiko: Limusa-Wiley.
7. Daniel C. Alexander, g. M. (2014). Elementär geometri för studenter. Cengage Learning.
8. Harpe, s. d. (2000). Ämnen i geometrisk gruppteori. University of Chicago Press.