En romboid Det är en platt figur på fyra sidor, -en quadrilateral -in som dess sidor och dess inre vinklar är olika två till två. Därför tillhör rhomboiden gruppen av sneda parallellogram.

Geometriska figurer är en del av naturen och särskilt de på fyra sidor som Rhomboid, har många tillämpningar inom arkitektur och design.

Figur 1. Belysningspanelerna i Allianz Arena Stadium i München, Tyskland, belyser med färgerna i det lokala laget och med vitt ljus när valet av det landet spelar. Källa: Pxhere.

UP Vi har en del av fasaden på Allianz Arena fotbollsarena i München. De är Rhomboid -paneler som lyser upp med färgerna på det lokala teamet.

Det är därför en figur med mycket visuell dynamik, för till skillnad från andra fyrkantiga har den ingen symmetriaxel. Följande figur visar olika romboider med olika orienteringar i planet.

figur 2. Flera romboid med olika orienteringar i planet. Källa: f. Zapata.

[TOC]

Skoidegenskaper

Därefter de viktigaste egenskaperna hos denna intressanta geometriska figur:

-Arknummer: 4.

-Antal vertikaler: 4.

-De motsatta sidorna är desamma och parallella, men de angränsande sidorna är ojämlika.

-Den har fyra inre vinklar: två akut (mindre än 90 °), betecknade med den grekiska bokstaven a och två stöt (över 180 °), kallad ß (se figur 3).

-Genom att lägga till två sammanhängande vinklar i romboiden erhålls 180º, därför är a och ß Tilläggs-.

-Summan av de fyra inre vinklarna är lika med 360º.

-En diagonal är ett segment som börjar från ett toppunkt och slutar på motsatt toppunkt.

-Den punkt där diagonalerna i Rhomboid -korsningen kallas barycenter.

-Rhomboiddiagonalerna har olika storlekar.

Om diagonalerna i romboiden finns det några viktiga detaljer som vi kommer att diskutera nedan.

Kan tjäna dig: i väntan på en linje: formel och ekvationer, representation, exempel

Rhomboids diagonaler

Det är mycket viktigt att betona att diagonalerna i romboiderna inte är bisektriska, det vill säga att de inte delar upp de inre vinklarna i figuren i två lika delar.

Diagonalerna är inte vinkelräta mot varandra. Vi kan dock enkelt beräkna dem med kosinus teorem. Således den huvudsakliga diagonalen D_M I rhomboiden i figur 3 är:

D_M = √ (a² + b² - 2.Ab.cos ß)

Och den mindre diagonala d_m Jag skulle vara:

D_m = √ (a² + b² - 2.Ab.cos α)

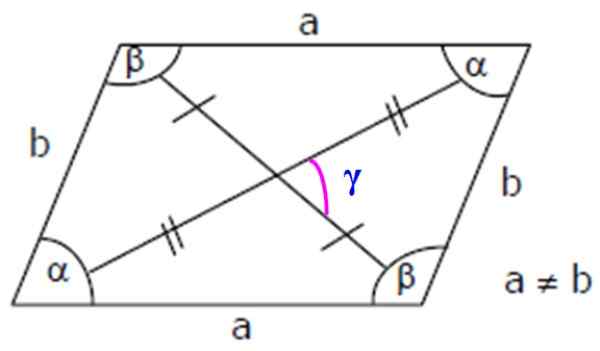Figur 3. Ringboidelement: sidor, inre och diagonala vinklar. Källa: Wikimedia Commons.

Viktig: Eftersom α och ß är kompletterande uppfylls det:

sin α = sin ß

cos α = -cos ß

Dessa egenskaper av trigonometriska skäl måste beaktas vid lösning av övningarna.

Hur man tar ut omkretsen och området

För att hitta omkretsen och det område vi kommer att ge namnet på sidorna på romboiden kommer dessa att vara till och b. Vi har också höjden på rhomboiden, kallad h, som är linjen som dras från en av vertikalerna och riktas vinkelrätt mot motsatt sida av figuren.

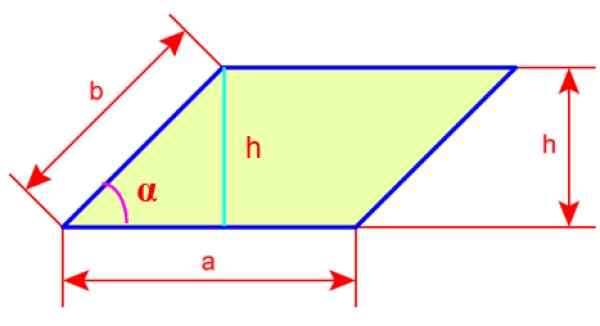Figur 4. Sidor och romboidhöjd. Källa: Wikimedia Commons.

Rhomboids omkrets

Rhomboidens omkrets beräknas genom att lägga till längderna på dess fyra sidor. Låt oss ringa P till omkretsen, då:

P = 2a + 2b

Vi kan också uttrycka det genom:

P = 2 (a+b)

Omkrets som känner till höjden

Om vi ​​ser bra ut kan höjden h bestämmas från triangeln till vänster i figur 4. Sidan B skulle vara hypotenusen och höjden H Cateto motsatt sig vinkeln a, därför:

sin α = motsatt / hypotenusa cateto

Nåväl:

sin α = h / b

Sedan rensar vi B:

b = h / sin a

Vi ersätter i omkretsen P:

P = 2 [A + (H / sin α)]

Spetsområde

Rhomboidområdet är måttet på ytan. Och eftersom det är ett parallellogram ges dess område A av det välkända uttrycket:

Kan tjäna dig: Vanlig faktor för grupperingsvillkor: Exempel, övningar

A = bas x höjd

Att enligt figurerna 3 och 4 uttrycks det genom:

A = a x h

Område som känner till båda sidor och en inre vinkel

Genom att tillämpa den grundläggande trigonometri från föregående avsnitt hittar vi motsvarande uttryck för Rhomboid -området:

H = B. synd

Då är området så här:

A = a. b. synd

Kom ihåg vad vi sa ovan om de kompletterande vinklarna, vi kan ersätta SEN α ​​med Sen ß vid behov.

Område som känner till diagonaler och vinkel mellan dem

Slutligen, om vi känner till diagonalerna D_M och D_m, Plus vinkeln γ mellan dem (se figur 3) kan området beräknas med diagonalerna i halvprodukten genom nämnda vinkel:

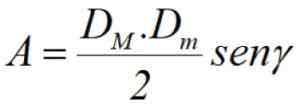
Träning löst

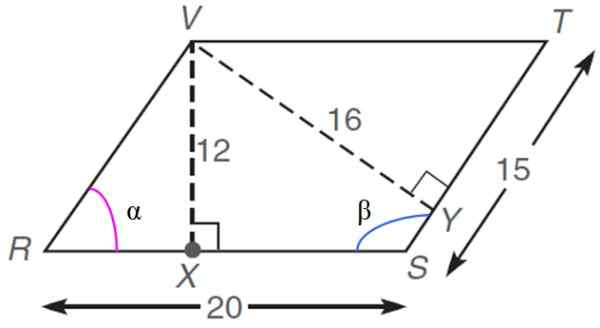
I följande romboid, vars dimensioner ges i godtyckliga enheter eller.till., hitta:

a) Omkretsvärdet

b) området

c) inre vinklar a och p

d) Längden på Rx -segmentet

e) måttet på var och en av diagonalerna

Lösning till

Omkretsen är:

P = 2 (a + b)

Vi identifierar först värdena på A och B:

A = 20

B = 15

Vi ersätter formeln och beräknar:

P = 2. (20 + 15) = 70 U.till.

Lösning B

Diagrammet ger höjd h = 12 u.A, därför kan området beräknas med formeln:

A = a x h

A = 20 x 12 u.till.² = 240 u.till.²

Oavsett den valda enheten för att mäta sidor och höjd uttrycks området alltid i kvadratiska enheter.

Samma resultat om du får när du beräknar området med den andra höjden på romboiden, vilket är värt 16 u.till. Verkligen:

A = 16 x 15 u.till.² = 240 u.till.²

Lösning C

Vinkeln α kan beräknas genom:

Det kan tjäna dig: positionsåtgärder, central tendens och spridning

H = B. synd

Eftersom H- och B -värden är kända därför:

α = Arcsen (H/B) = Arcsen (12/15) = 53.13th

Kom ihåg att a- och ß -vinklar är kompletterande, det är uppfyllt:

α + β = 180º ⇒ β = 180 - 53.13: e = 126.87º

Lösning D

RX -segmentlängden beräknas enkelt, eftersom det finns tillräckligt med information för att hitta den. Till exempel genom:

Rx = RV . cos α = 15 . Cos 53.13: e u.till. = 9 u.till.

Också genom Pythagoras teorem genom rektangelns triangel på sidorna 15 och 12 u.till:

(RV)² = (Rx)² + h²

Rensa längden på räntesegmentet:

Rx = √ [(RV)² - h²] = √ [15² - 12²] = √81 = 9

Lösning E

Måttet på en av diagonalerna, till exempel diagonalen som förenar vertikalerna R och T, som är en viktig diagonal, ges av kosinussteoremet, som tidigare förklarats, så vi ersätter värden där:

D_M = √ (20² + 25² - 2. tjugo. femton .Cos 126.87º) = 37.22 U.till.

För den mindre diagonalen:

D_m = √ (20² + 25² - 2. tjugo. femton .Cos 53.13: e) = 25.79 U.till.

Referenser

1. Alexander, D. 2013. Geometri. Femte. Utgåva. Cengage Learning.
2. Baldor, a. 1973. Geometri och trigonometri. Centralamerikansk kulturell redaktion.
3. OCH. TILL. 2003. Geometrielement: med övningar och kompassgeometri. University of Medellin.
4. Jiménez, r. 2010. Matematik II. Geometri och trigonometri. Andra upplagan. Prentice hall.
5. Regelbundna polygoner. Återhämtad från: kompis.teknik.USAC.Edu.Gt.
6. Universumsformler. Romboid. Återhämtat sig från: universalformulor.com.
7. Wikipedia. Romboid. Återhämtad från: är.Wikipedia.org.