Proportionell variation

Vad är proportionell variation?

Den proportionella variationen mellan två variabler "x" och "y" sker när, genom att multiplicera en av dem med en konstant, den andra också multipliceras eller divideras med samma konstant. Många verkliga situationer kan beskrivas korrekt med dem.

Proportionaliteten mellan variablerna kan vara direkt eller omvänd. I direkt proportionalitet är förhållandet av typen:

y = k ∙ x

Eller motsvarande:

K = y/x

Där k är en konstant som kallas proportionalitetskonstant antingen proportionalitetsförhållande. Observera att om "X" ökar "gör det i samma andel, och om" X "minskar kommer det också" Y ". När förhållandet mellan variablerna är grafer erhålls en rak linje som går igenom koordinatsystemets ursprung (se övningen löstes senare).

Den direkta variationen kan också ske mellan en variabel och en kraft av den andra, till exempel "Y" kan vara direkt proportionell mot x², x³ och så.

Å andra sidan, i omvänd proportionalitet, är variablerna kopplade genom uttrycket:

x ∙ y = k

Detta uttryck betyder att produkten av variablerna är en konstant. När du graferar förhållandet mellan variablerna är en hyperbola. Om produkten av en variabel med den ena effekten är konstant, representerar den också ett fall av omvänd proportionalitet, till exempel:

x²∙ y = k; x³∙ y = k ..

Exempel

En tillämpning av proportionell variation är kartlayout

Många lagar om fysik och kemi uttrycks matematiskt som proportioner. Till exempel kraften som utövar en fjäder och förlängning av samma, förhållandet mellan trycket och volymen i en gas vid konstant temperatur, perioden för en enkel pendel och kvadratroten av dess längd och många fler. Genom att känna till modellen som styr fenomenet kan du ta reda på ditt beteende för alla värde på variablerna.

Kan tjäna dig: existens och unikhetsteorem: demonstration, exempel och övningar

Och inte bara det, de gäller också i otaliga situationer som dessa:

• Passera mönstret för ett plagg av en mindre storlek till en större storlek (eller vice versa).
• I omvandlingsfaktorer, för att flytta från en enhet till en annan, till exempel kilometer till mil, gallon till liter och mer.
• Beräkna ingredienserna i ett recept för 6 personer som känner till kravet på 4 personer.
• Bestämma beloppet för vissa skatter i enlighet med de erhållna inkomsterna.
• Vid beräkningen av enkelt intresse.
• När du ritar plan i skala.
• När du måste beräkna priset på en mängd produkter som känner till enhetspriset.
• I likheten mellan trianglar.

Därefter finns det i detalj två intressanta situationer där proportionella variationer gäller:

Exempel 1

På skalan av en stad mäter Hermitage Avenue 3.2 cm, är den verkliga längden på 400 m. Å andra sidan måste gatan i La Fuente, som verkligen mäter 180 m lång med en proportionellt kortare slag. Vad är storleken på slaget?

Uttalandet erbjuder den fullständiga informationen från Ermita Avenue: Låt den verkliga längden på avenyn och ℓ dess längd på planet, eftersom variationen är av direkt proportionalitet, måste den:

L = k ∙ ℓ

Från uppgifterna på Hermitage Avenue kan du veta värdet på proportionalitetskonstanten K, men innan det är nödvändigt att lämna alla längder i samma enheter:

3.2 cm = 0.032 m

Så:

400 m = k ∙ 0.032 m

Därför är proportionalitetskonstanten:

Kan tjäna dig: Vilka är elementen i liknelsen? (Delar)

K = 400/0.032 = 12500

Nu är det känt att:

L = 12500 ∙ ℓ

Detta resultat tolkas på följande sätt: gatornas längd på denna karta är 12500 gånger mindre än dess verkliga längd. Därför mäter linjen i La Fuente -mätningen:

ℓ = 180 m/ 12500 = 0.0144 m = 1.44 cm

Exempel 2

En analytiker har följande värdentabell för variablerna "X" och "Y" som erhållits experimentellt och vill veta om dessa data passar en modell med direkt proportionell variation eller en av omvänd proportionell variation.

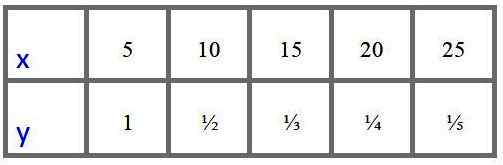
Vad ska du göra för att veta?

För det första observeras det att när "x" ökar, "y" minskar, så det misstänker en omvänd proportionalitet, i alla fall, för att säkerställa att analytikern har möjlighet att bedöma om kvoten och/x är konstant (proportionell variation direkt) eller om produkt x.och är konstant (omvänd proportionell variation).

Testning med det första alternativet:

1 ÷ 5 = 0.2

½ ÷ 10 = 0.05

⅓ ÷ 15 = 0.022 ..

Det dras slutsatsen att det inte är en direkt proportionell variation, eftersom kvoten och/x ger olika värden för varje par data.

Vi måste kontrollera om produkten x ∙ är konstant:

5 × 1 = 5

10 × ½ = 5

15 × ⅓ = 5

20 × ¼ = 5

25 × ⅕ = 5

Och som produkten x ∙ y = 5 dras slutsatsen att variationen är av omvänd proportionalitet.

Denna information tjänar till att känna till värden som inte finns i tabellen, till exempel, vad skulle vara värdet av "y" när x = 30?

Från x ∙ y = 5, "y" rensas och ersätts x = 30:

y = 5/x

y = 5/30 = 1/6

Träning löst

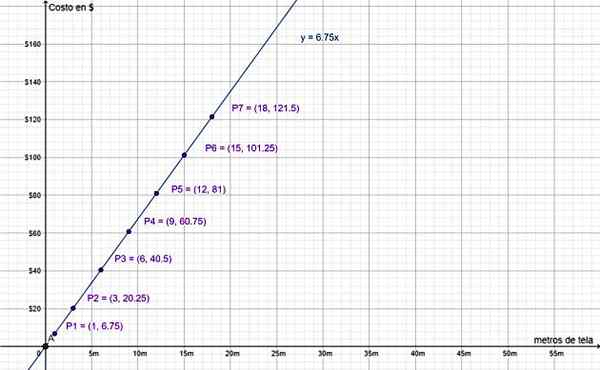
Om en tygmätare kostar 6.75 $ och att veta att priset är direkt proportionellt mot mängden meter att köpa, hitta:

Det kan tjäna dig: antiderivativ: formler och ekvationer, exempel, övningar

a) Det algebraiska uttrycket som länkar variablerna "pris till $" och "antal meter tyg".

b) Förbered en tabell över värden med priser för 3, 6, 9, 12, 15 och 18 meter tyg.

c) grafer de erhållna värdena.

Svara på

Låt "y" det variabel "priset på $" och "x" den variabla "mängden mätare av tyg". Som direkt är proportionella måste du:

y = k ∙ x

För x = 1 meter, y = 6.75 $, därför k = 6.75 $/meter. Detta är enhetspriset för tyget, priset på något annat "X" -tyg erhålls genom att multiplicera med detta värde, då är det sökte algebraiska uttrycket:

y = 6.75 ∙ x

Svar B

Värdentabellen med priser till $ för 3, 6, 9, 12, 15 och 18 meter är:

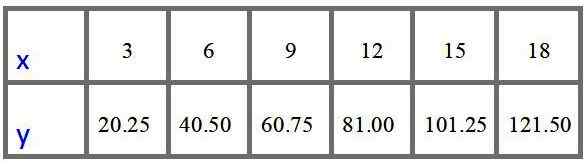
Svar C

Slutligen bekräftar grafen över värdena i föregående tabell att det är en direkt proportionell variation:

Kostnaden till $ och mängden meter tyg är direkt proportionella mängder. Källa: f. Zapata.

Observera att värdet (0,0) ingår, eftersom linjen y = 6.75 ∙ x passerar genom koordinatsystemets ursprung, som förklarats tidigare. Det är meningsfullt, eftersom det inte är ett köp motsvarande att köpa 0 m tyg, vars värde är 0 $.

Referenser

1. Larson, r. 2012. Förskulptur. 8th. Utgåva. Cengage Learning.
2. Mexikos sekretariat. Den proportionella variationen. Hämtad från: PPS.K12.Eller.oss.
3. Stewart, J. 2007. Förberäkning: Matematik för beräkning. Femte. Utgåva. Cengage Learning.
4. Unk. Studieguider: Matematik i. Återhämtat sig från: Dirre.Unk.mx.
5. Zill, D. 2008. Förberäkning med beräkningsförskott. 4th. Utgåva. McGraw Hill.