Vector Director Equation of the Line, lösta övningar
- 3766
- 742
- PhD. Lennart Johansson
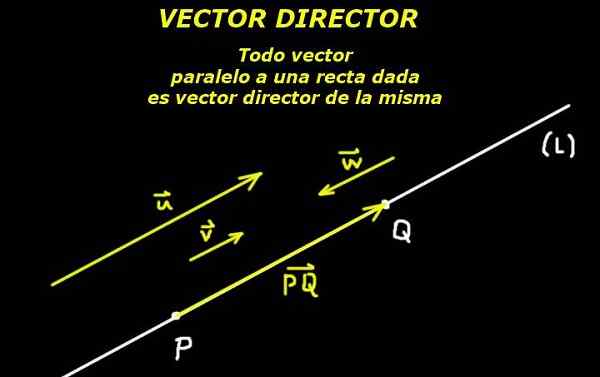
Det förstås av Regissörvektor den som definierar riktningen för en linje, antingen i planet eller i rymden. Därför kan en vektor som är parallell med linjen betraktas som en chef för samma.
Detta är möjligt tack vare ett axiom av euklidisk geometri som säger att två punkter definierar en linje. Sedan definierar det orienterade segmentet som bildar dessa två punkter också en vektordirektör för den linjen.
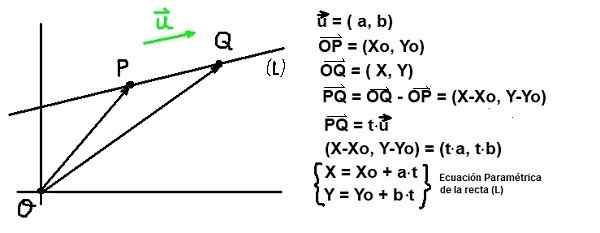
Figur 1. Vektorchef för en linje. (Egen utarbetande) Med tanke på en punkt P tillhör linjen (L) och med tanke på en regissörvektor eller Av den linjen är linjen helt bestämd.
[TOC]
Linjens ekvation och direktörschef
figur 2. Linjens ekvation och direktörschef. (Egen utarbetande) Med tanke på en punkt P av koordinater F: (xo, jag) och en vektor eller Chef för en linje (L), Hela punkten Q av koordinater F: (x, y) måste uppfylla att vektorn Pq vara parallell med u. Detta sista villkor garanteras om Pq Det är proportionellt mot eller:
Pq = T⋅eller
I det föregående uttrycket t Det är en parameter som tillhör riktiga siffror.
Om de kartesiska komponenterna i Pq och av eller Den tidigare ekvationen är skriven enligt följande:
(X-xo, y-yo) = t⋅ (a, b)
Om komponenterna i vektorjämlikheten är lika med följande par av ekvationer:
X - xo = a⋅t och Och - mig = b⋅t
Parametrisk ekvation av linjen
Koordinaterna X och OCH av en punkt som tillhör linjen (L) som går igenom en koordinatpunkt (Xo, jag) Och det är parallellt med Regissörvektor eller= (a, b) De bestäms genom att tilldela verkliga värden till den variabla parametern t:
X = xo + a⋅t; Y = me + b⋅t
Exempel 1
För att illustrera betydelsen av den parametriska ekvationen för linjen tar vi som Director Vector
Kan tjäna dig: böljande optikeller = (a, b) = (2, -1)
Och som en känd punkt i linjen
P = (xo, me) = (1, 5).
Linjens parametriska ekvation är:
X = 1 + 2⋅t; Y = 5 - 1⋅t; Som
För att illustrera innebörden av denna ekvation visar figur 3, där parameter t ändrar värde och punkt Q av koordinater (X, y) Ta olika positioner på linjen.
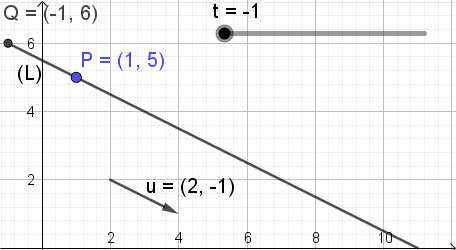Figur 3. Pq = t u. (Egen utarbetande) Linjen i vektorform
Med tanke på en punkt P i linjen och dess direktör eller ekvationen för linjen kan skrivas i en vektorform:
O Q = Op + λ⋅eller
I den föregående ekvationen som är någon punkt men tillhör linjen och λ Ett riktigt nummer.
Linjens vektorekvation är tillämplig på valfritt antal dimensioner, till och med en hyper-ERET kan definieras.
I det tre dimensionella fallet för en regissörvektor eller= (a, b, c) och en punkt P = (xo, jag, zo), Koordinaterna för en generisk punkt Q = (x, y, z) Att tillhöra linjen är:
(X och z) = (Xo, i, zo) + λ⋅ (a, b, c)
Exempel 2
Tänk igen den linje som har som regissör för regissör
eller = (a, b) = (2, -1)
Och som en känd punkt i linjen
P = (xo, me) = (1, 5).
Vektorekvationen för denna linje är:
(X, y) = (1, 5) + λ⋅ (2, -1)
Kontinuerlig form av linjen och regissörens vektor
Från den parametriska formen, rensa och matcha parametern λ har du:
(X-xo)/a = (y-yo)/b = (z-zo)/c
Detta är den symmetriska formen för linjeekvationen. Jag känner att till, b och c De är komponenterna i regissörens vektor.
Exempel 3
Tänk på linjen som har som regissör för regissör
eller = (a, b) = (2, -1)
Och som en känd punkt i linjen
Kan tjäna dig: vad är elen? (Med experiment)P = (xo, me) = (1, 5). Hitta dess symmetriska form.
Den symmetriska eller kontinuerliga formen är av linjen är:
(X - 1)/2 = (y - 5)/( - 1)
Allmän form av linjeekvationen
Det är känt som den allmänna formen av linjen i XY -planet till ekvationen som följande struktur har:
A⋅x + b⋅y = c
Uttrycket av den symmetriska formen kan skrivas om så att den har den allmänna formen:
B⋅x - a⋅y = b⋅xo - a⋅o
Jämförelse med den allmänna formen av linjen återstår:
A = b, b = -a och C = B⋅XO - A⋅O
Exempel 3
Hitta den allmänna formen av linjen vars regissör är u = (2, -1)
Och vad som går igenom punkt P = (1, 5).
För att hitta den allmänna formen kan vi använda de givna formlerna, men en alternativ väg kommer att väljas.
Vi börjar med att hitta den dubbla vektorn för U -vektorn, definierad som vektorn som erhålls genom att utbyta komponenterna i U och multiplicera med -1 den andra:
W= (-1, -2)
Den dubbla vektorn W motsvarar en rotation 90 ° i schemat för direktörens direktör v.
Vi multiplicerar klättring W med (X, y) och med (Xo, jag) Och vi matchar:
(-1, -2) • (x, y) = (-1, -2) • (1, 5)
-X -2y = -1 -2⋅5 = -11
Äntligen kvar:
X + 2y = 11
Standardform för linjekvationen
Det är känt som standardform av linjen i XY -planet, den som har följande struktur:
Y = m⋅x + d
där m representerar lutningen och d -avlyssningen med axeln och.
Med tanke på regissören u = (a, b) vektor är lutningen m b/a.
Och D erhålls genom att ersätta X och Y av den kända punkten Xo, mig:
I = (b/a) xo + d.
Kort sagt, m = b/a y d = me -(b/a) xo
Observera att lutningen M är kvoten mellan komponenten och av regissören och komponenten x av samma.
Kan tjäna dig: rotationsbalans: formler och ekvationer, exempel, övningarExempel 4
Hitta standardformen på linjen vars regissör är u = (2, -1)
Och vad som går igenom punkt P = (1, 5).
M = -½ och d = 5 -( -½) 1 = 11/2
Y = (-1/2) x + 11/2
Löst övningar
-Övning 1
Hitta en vektordirektör för linjen (L) som är skärningspunkten mellan planet (π): x - y + z = 3 och planet (ω): 2x + y = 1.
Skriv sedan den kontinuerliga formen av linjen (L).
Lösning
Från planekvationen (ω) clearance y: y = 1 -2x
Sedan ersätter vi i planekvationen (π):
X - (1 - 2x) + z = 3 ⇒ 3x + z = 4 ⇒ z = 4 - 3x
Sedan parametrerar vi x, vi väljer parametrering x = λ
Detta innebär att linjen har en vektorekvation som ges av:
(X, y, z) = (λ, 1 - 2λ, 4 - 3λ)
som kan skrivas om som:
(X, y, z) = (0, 1, 4) + λ (1, -2, -3)
Med vad som är tydligt att vektorn eller = (1, -2, -3) är en rak hanteringsvektor (L).
Den kontinuerliga formen av linjen (L) är:
(X - 0)/1 = (y - 1)/( - 2) = (z - 4)/( - 3)
-Övning 2
Med tanke på 5x -planet + till Y + 4z = 5
och linjen vars ekvation är x/1 = (y-2)/3 = (z -2)/(-2)
Bestämma värdet på till så att planet och linjen är parallella.
Lösning 2
Vektorn n = (5, A, 4) är en normal vektor för planet.
Vektorn eller = (1, 3, -2) är en rak chef.
Om linjen är parallell med planet, då n • v = 0.
(5, till, 4)•(1, 3, -2) = 5 +3till -8 = 0 ⇒ till= 1.
Referenser
- Fleming, w., & Varberg, D. OCH. (1989). Prealculus matematik. Prentice Hall PTR.
- Kolman, f. (2006). Linjär algebra. Pearson Education.
- Lojal, j. M., & Viloria, n. G. (2005). Platt analytisk geometri. Mérida - Venezuela: Venezuelansk redaktion C. TILL.
- Navarro, Rocio. Vektorerna. Återhämtat sig från: böcker.Google.co.gå.
- Pérez, c. D. (2006). Prequalculus. Pearson Education.
- Prenowitz, w. 2012. Grundläggande geometri. Rowman & Littlefield.
- Sullivan, m. (1997). Prequalculus. Pearson Education.