Normal beräkning och exempelvektor

han Normalvektor Det är en som definierar riktningen vinkelrätt mot en geometrisk enhet som beaktas, som kan vara för en kurva, ett plan eller en yta, till exempel.

Det är ett mycket användbart koncept i positioneringen av en mobil partikel eller någon yta i rymden. I följande graf är det möjligt att se hur den normala vektorn är till en godtycklig kurva C:

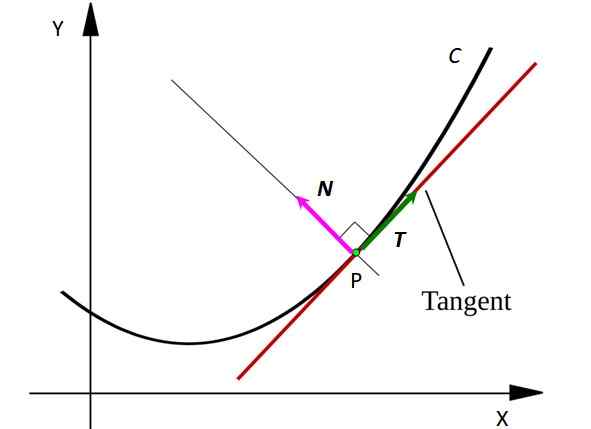
Figur 1. En C -kurva med den normala vektorn till kurvan vid punkt P. Källa: SVJO [CC BY-SA 3.0 (https: // CreativeCommons.Org/licenser/BY-SA/3.0)]

Tänk på en punkt P på kurvan C. Poängen kan representera en mobil partikel som rör sig efter en C -formad väg. Linjen tangent till kurvan vid punkt P verkar ritad i rött.

Observera att vektorn T Det är tangent att c vid varje punkt, medan vektorn N är vinkelrätt mot T och pekar på mitten av en imaginär omkrets vars båge är ett segment av C. Vektorer betecknas i djärv bokstav i tryckt text för att skilja dem från andra icke -vektorstorlekar.

Vektorn T Det indikerar alltid var partikeln rör sig, därför indikerar den hastigheten på samma. Istället vektorn N Peka alltid i den riktning som partikeln vänder, på detta sätt indikerar det konkaviteten för C -kurvan.

[TOC]

Hur man får den normala vektorn till ett plan?

Den normala vektorn är inte nödvändigtvis en enhetsvektor, det vill säga en vektor vars modul är 1, men i så fall kallas den normal enhetsvektor.

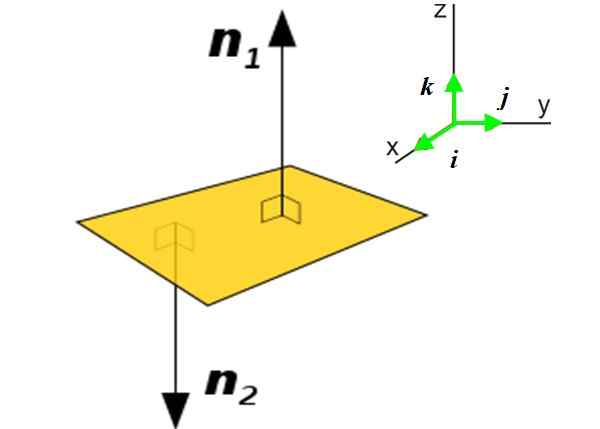
figur 2. Till vänster ett P -plan och de två normala vektorerna till nämnda plan. Till höger enhetsvektorerna i de tre riktningarna som bestämmer utrymmet. Källa: Wikimedia Commons. Se sidan för författare [Public Domain]

I många applikationer är det nödvändigt att känna till den normala vektorn till ett plan istället för en kurva. Denna vektor gör känd orienteringen av nämnda plan i rymden. Tänk till exempel på planet P (gul) av figuren:

Det kan tjäna dig: Gemine: Origins, Egenskaper och hur man observerar dem

Det finns två normala vektorer till det planet: n₁ och n₂. Användningen av det ena eller det andra beror på det sammanhang i vilket nämnda plan finns. Att få den normala vektorn till ett plan är mycket enkelt om ekvationen är känd:

Ax + av + cz + d = 0, med till, b, c och d riktiga nummer.

Tja, en normal planvektor ges av:

N = a Yo + b J + c k

Här vektorn N uttrycks i termer av enhetsvektorerna och vinkelrätt mot varandra Yo, J och k, riktad genom de tre riktningarna som bestämmer utrymmet X och z, Se figur 2 till höger.

Den normala vektorn från vektorprodukten

En mycket enkel procedur för att hitta den normala vektorn använder sig av vektorproduktens egenskaper mellan två vektorer.

Som känt, tre olika punkter och inte kolineala med varandra, bestäm ett P -plan. Nu är det möjligt att få två vektorer eller och v som tillhör nämnda plan med dessa tre poäng.

När vektorerna är, Vektorprodukt eller x v Det är en operation vars resultat är en vektor, som har egenskapen att vara vinkelrätt mot planet bestäms av eller och v.

Känd denna vektor, det betecknas som N, Och från det kommer det att vara möjligt att bestämma planets ekvation tack vare ekvationen som anges i föregående avsnitt:

N = eller x v

Följande figur illustrerar den beskrivna proceduren:

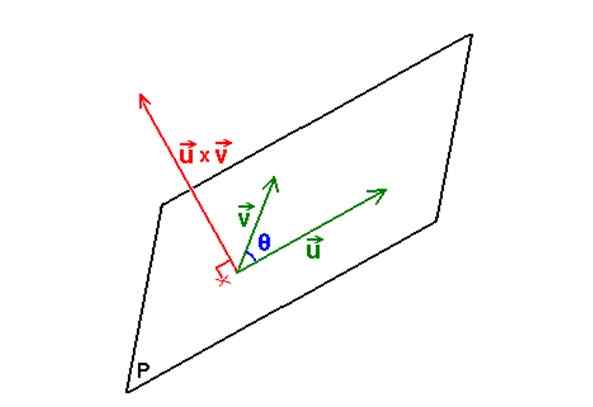Figur 3. Med två vektorer och deras vektor eller tvärprodukt bestäms ekvationen för planet som innehåller de två vektorerna. Källa: Wikimedia Commons. Ingen maskinläsbar författare tillhandahållen. M.Romero Schmidtke antog (baserat på upphovsrättsanspråk). [Allmängods]

Exempel

Hitta ekvationen för planet bestämd med punkter A (2,1,3); B (0,1,1); C (4,2,1).

Kan tjäna dig: kontinuitetsekvation

Lösning

Denna övning illustrerar proceduren som beskrivs ovan. Genom att ha 3 poäng väljs en av dem som ett vanligt ursprung för två vektorer som tillhör planet definierat av dessa punkter. Till exempel är punkt A inställt som ursprung och vektorer byggs Ab och Växelström.

Vektorn Ab Det är vektorn vars ursprung är punkt A och vars slut är punkt B. Vektors koordinater Ab Koordinaterna för B för koordinaterna för A:

Ab = (0-2) Yo + (1-1) J + (1-3) k = -2Yo + 0J -2 k

Fortsätt på samma sätt för att hitta vektorn Växelström:

Växelström = (4-2) Yo + (2-1) J + (1-3) k = 2Yo + J -2 k

Vektorproduktberäkning Ab x ac

Det finns flera procedurer för att hitta vektorprodukten mellan två vektorer. I det här exemplet används en mnemonisk procedur som använder följande siffra för att hitta vektorprodukter bland enhetsvektorer Yo, J och K:

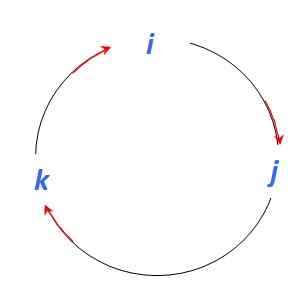Figur 4. Grafik för att bestämma vektorprodukten mellan enhetsvektorerna. Källa: Självgjord.

För att starta är det bra att komma ihåg att vektorprodukter mellan parallella vektorer är ogiltiga därför:

Yo x Yo = 0; J x J = 0; k x k = 0

Och eftersom vektorprodukten är en annan vektor vinkelrätt mot de deltagande vektorerna, rör sig i riktning mot den röda pilen du har:

Yo x J = k ; J x k = Yo; k x Yo = J

Om du måste röra dig i motsats till pilen läggs ett skylt (-):

J x Yo = - k; k x J = -Yo; Yo x k = -J

Totalt är det möjligt att tillverka 9 vektorprodukter med enhetsvektorerna Yo, J och k, varav 3 kommer att bli ogiltiga.

Ab x Växelström = (-2Yo + 0J -2 k) X (2Yo + J -2 k) = -4 (Yo x Yo) -2 (Yo x J) +4 (Yo x k) +0 (J x Yo) + 0 (J x J) - 0 (J x k) - 4 (k x Yo) -2 (k x J) + 4 (k x k) = -2k-4J-4J+2Yo = 2Yo -8J-2k

Flygekvation

Vektor N har bestämts av vektorprodukten som tidigare beräknats:

Kan tjäna dig: pendular rörelse

N = 2Yo -8J-2k

Därför är a = 2, b = -8, c = -2, den sökta planen:

Ax + av + Cz + D = 0 → 2x-8y-2Z + D = 0

Värdet av d. Detta är enkelt om värdena på någon av punkterna A, B eller C är tillgängliga ersätts i planekvationen. Att välja C till exempel:

x = 4; y = 2; Z = 1

Är kvar:

2.4 - 8.2 - 2.1 + D = 0

-10 + d = 0

D = 10

Kort sagt, det önskade planet är:

2x-8y-2Z +10 = 0

Den nyfikna läsaren kan fråga om samma resultat skulle ha erhållits om istället för att göra Ab x Växelström Det skulle ha valts Växelström x Ab. Svaret är ja, planet bestäms av dessa tre punkter är unikt och har två normala vektorer, som visas i figur 2.

När det gäller den valda punkten som vektors ursprung finns det inte heller något besvär att välja någon av de andra två.

Referenser

1. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volym 1. Kinematik. Redigerad av Douglas Figueroa (USB). 31-62.
2. Hitta det normala för ett plan. Hämtad från: webben.ma.Utexas.Edu.
3. Larson, r. (1986). Beräkning och analytisk geometri. MC Graw Hill. 616 - 647.
4. Linjer och planer i R 3. Återhämtat sig från: matematik.Sköre.Edu.
5. Normalvektor. Återhämtat sig från Mathworld.Volfram.com.