Resulterande vektorberäkning, exempel, övningar

han resulterande vektor Det är den som erhålls av en operation med vektorer vars resultat också är en vektor. Normalt är denna operation summan av två eller flera vektorer, genom vilken en vektor erhålls vars effekt är ekvivalent.

På detta sätt erhålls vektorer som hastighet, acceleration eller kraft resulterande. Till exempel när flera krafter agerar på en kropp F₁, F₂, F₃,.. . Vektorsumman av alla dessa krafter motsvarar nettokraften (den resulterande), som matematiskt uttrycker sig:

F₁ + F₂ + F₃ +... = F_R  antingen F_N

Figur 1. Snövikt distribueras över taket och dess verkan kan ersättas av en enda resulterande kraft som appliceras på rätt plats. Källa: Pixabay.

Den resulterande vektorn, oavsett om det är krafter eller någon annan vektorstorlek, är att tillämpa reglerna för summan av vektorer. Eftersom vektorer har riktning och känsla utöver numeriskt värde räcker det inte att lägga till modulerna för att ha den resulterande vektorn.

Detta gäller endast i det fall där vektorerna är i samma riktning (se exempel). Annars är det nödvändigt att använda vektorsummetoder, som beroende på fall kan vara geometriska eller analytiska.

[TOC]

Exempel

Geometriska metoder för att hitta den resulterande vektorn är polygonmetoden och parallellogrammetoden.

När det gäller analysmetoderna är komponentmetoden, genom vilken vektorn som är resultatet av alla vektorsystem kan hittas, så länge vi har dess kartesiska komponenter.

Geometriska metoder för att lägga till två vektorer

Anta att vektorerna eller och v (Vi betecknar dem med fetstil för att skilja dem från skalaren). I figur 2) har vi dem belägna på planet. I figur 2 b) har den flyttat till vektor V på ett sådant sätt att dess ursprung sammanfaller med slutet av eller. Den resulterande vektorn går från ursprunget till den första (eller) till spetsen på det sista (v):

Det kan tjäna dig: Kompressibilitet: fasta ämnen, vätskor, gaser, exempel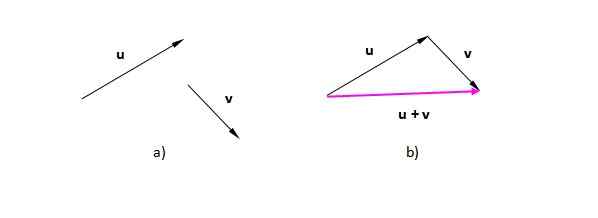 figur 2. Den resulterande vektorn från den grafiska summan av vektorer. Källa: Självgjord.

Siffran som resulterar i detta fall är en triangel (en triangel är en 3 -sidad polygon). Om vi ​​har två vektorer i samma riktning är proceduren densamma: placera en av vektorerna efter den andra och rita en som går från ursprunget eller svansen till den första till spetsen eller slutet av det sista.

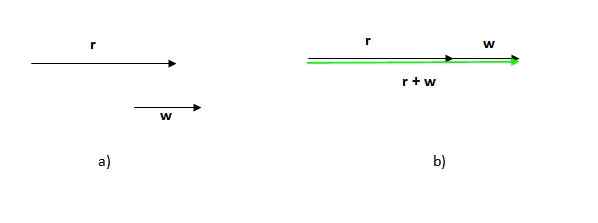
Observera att ordningen i vilken denna procedur görs inte spelar någon roll, eftersom summan av vektorer är kommutativ.

Observera också att i detta fall modul (Längden eller storleken) för den resulterande vektorn är summan av modulerna för de ytterligare vektorerna, till skillnad från det föregående fallet, där den resulterande vektormodulen är mindre än summan av deltagarnas moduler.

Parallellogrammetod

Denna metod är mycket lämplig när du behöver lägga till två vektorer vars ursprungspunkter är överens, med ursprunget till ett X-Y-koordinatsystem. Anta att detta är fallet med våra vektorer eller och v (Bild 3):

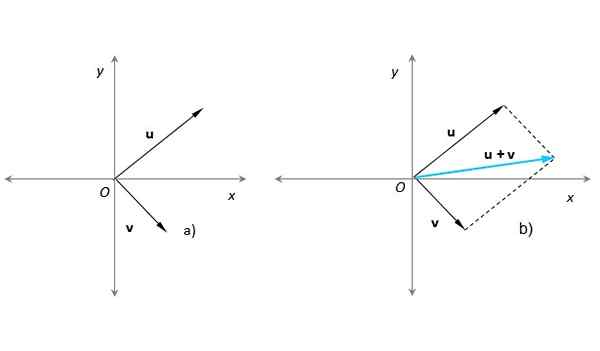Figur 3. Summan av två vektorer med hjälp av parallellogrammetoden med den resulterande vektorn i turkosblå. Källa: Självgjord.

I figur 3b) har ett parallellogram byggts med hjälp av parallella streckade linjer till eller redan v. Den resulterande vektorn har sitt ursprung i O och dess slut vid den punkt där de streckade linjerna korsar varandra. Denna procedur är helt motsvarande den som beskrivs i föregående avsnitt.

Övningar

-Övning 1

Med tanke på följande vektorer, hitta den resulterande vektorn med den polygonala metoden.

Det kan tjäna dig: lätt reflektion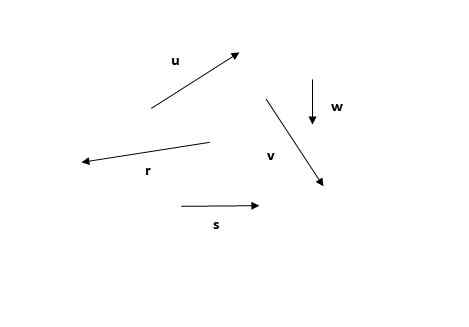 Figur 4. Vektorer för att hitta dess resulterande genom den polygonala metoden. Övning 1. Källa: Självgjord.

Lösning

Den polygonala metoden är den första av de metoder som ses. Kom ihåg att summan av vektorer är kommutativ (tilläggsordningen ändrar inte summan), så du kan börja med någon av vektorerna, till exempel eller (Bild 5A) eller r (Bild 5B):

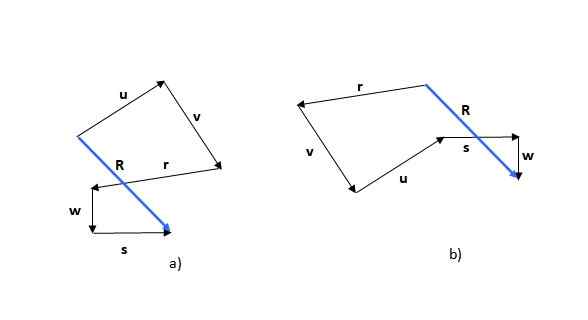Figur 5. Summan av vektorer genom den polygonala metoden. Källa: Självgjord.

Den erhållna figuren är en polygon och den resulterande vektorn (i blått) kallas R. Om du börjar med en annan vektor kan figuren som bildas vara annorlunda, vilket kan ses i exemplet, men den resulterande vektorn är densamma.

Övning 2

I följande figur är det känt att vektorns moduler eller och v respektive är U = 3 godtyckliga enheter och V = 1.8 godtyckliga enheter. Vinkeln som eller form med den positiva x -axeln är 45 º, medan v Form 60 º med y -axeln, som ses i figuren. Hitta den resulterande vektorn, storleken och riktningen.

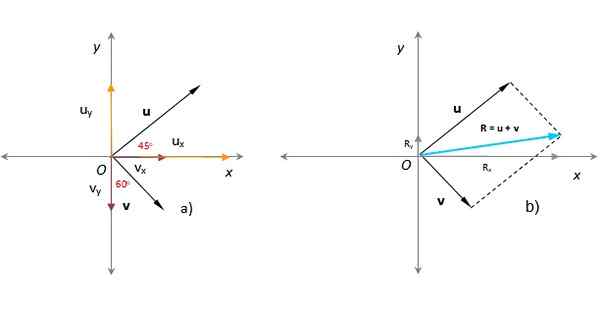
Lösning

I föregående avsnitt hittades den resulterande vektorn som applicerade parallellogrammetoden (i turkos i figuren).

Ett enkelt sätt att hitta den resulterande vektorn analytiskt är att uttrycka vektorerna som lägger till i termer av deras kartesiska komponenter, vilket är en enkel uppgift när modul och vinkel är kända, till exempel vektorerna i detta exempel:

eller_x = u . cos 45º = 3 x cos 45 º = 2.12; eller_och = u . Synd 45 º = 3x Sen 45º = 2.12

v_x = v . Sen 60º = 1.8 x Sen 60 º = 1.56; v_och = -V . cos 60 º = -1.8 x cos 60º = - 0.9

Kan tjäna dig: pendular rörelse

Vektorerna eller och v De är vektorer som tillhör planet, med båda två komponenter vardera. U -vektorn är i den första kvadranten och dess komponenter är positiva, medan vektor V är i den fjärde kvadranten; Dess X -komponent är positiv, men dess projektion på den vertikala axeln faller i axeln och negativ.

Beräkning av de kartesiska komponenterna i den resulterande vektorn

Den resulterande vektorn lägger till algebraiskt respektive komponenter x och y för att erhålla sina kartesiska komponenter:

R_x = 2.12 + 1.56 = 3.68

R_och = 2.12 + (-0.9) = 1.22

När de kartesiska komponenterna har specificerats och vektorn är känd helt. Den resulterande vektorn kan uttryckas med notationen inom fyrkantiga parenteser (parentes):

R = godtyckliga enheter

Konsolen används för att skilja en vektor från en punkt i planet (eller i rymden). Ett annat sätt att uttrycka den resulterande vektorn på ett analytiskt sätt är genom användning av enhetsvektorer Yo och J på planet (Yo, J och k i rymden):

R = 3.68 Yo + 1.22 J godtyckliga enheter

Eftersom båda komponenterna i den resulterande vektorn är positiva, vektorn R Det tillhör den första kvadranten, som redan hade sett grafiskt.

Den resulterande vektorns storlek och riktning

Känd för kartesiska komponenter beräknas storleken på R genom Pythagoras teorem, eftersom den resulterande vektorn R, Bredvid dess komponenter r_x och r_och De bildar en höger triangel:

Storlek eller modul: r = (3.68² + 1.22²)^½ = 3.88

Adress Q Tar den positiva X -axeln som referens: Q = Arcan (R_och / R_x) = arctg (1.22/3.68) = 18.3: e

Referenser

1. Lägga till vektorer och regler. Återhämtat sig från: newt.Fysik.Unsw.Edu.Au
2. Figueroa, D. Serie: Physics for Science and Engineering. Volym 1. Kinematik.31-68.
3. Fysisk. Modul 8: Vektorer. Återhämtat sig från: frtl.Utn.Edu.ar
4. Hibbeler, R. 2006. Mekanik för ingenjörer. Statisk. Sjätte upplagan. Continental Editor Company. 15-53.
5. Tilläggskalkylatorvektor. Återhämtat sig från: www.1728.org