Colineal vektorer

Vi förklarar vad colineala vektorer är, Colineal Vectors -systemet och vi lägger flera exempel

Vilka är de kollineala vektorerna?

De Colineal vektorer De är en av de tre typerna av befintliga vektorer. Det här är de vektorer som är i samma riktning eller handlingslinje. Detta betyder följande: Två eller flera vektorer kommer att vara colineal om det finns fallet att de är ordnade i rader som är parallella med varandra.

En vektor definieras som en storlek som appliceras på en kropp och kännetecknas av att ha en riktning, en känsla och en skala. Vektorer finns i planet eller i rymden och kan vara av olika typer: colineala vektorer, samtidiga vektorer och parallella vektorer.

När är det kollineala vektorer?

Vektorerna är colineal om handlingslinjen är exakt samma handlingslinje för alla andra vektorer, oavsett storlek och riktning för var och en av vektorerna.

Vektorer används som representationer inom olika områden som matematik, fysik, algebra och även i geometri, där vektorer är kolineala endast när deras riktning är densamma, oavsett att deras betydelse inte är.

Exempel på kolineala vektorer

• Två eller flera vektorer är colineala om förhållandet mellan koordinater är detsamma.

Exempel 1

Du har vektorer M = m_x; m_y och n = n_x; N_. Dessa är kollinära om:

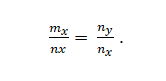
Exempel 2

Det kan bestämmas om vektorerna j = 3,6,15 och p = 1,2,5 är kollinära genom förhållandet mellan deras koordinater, som du måste vara proportionell mot varandra; det vill säga: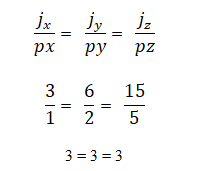

• Två eller flera vektorer är colineala om produkt- eller vektormultiplikationen är lika med noll (0). Detta beror på att i koordinatsystemet kännetecknas varje vektor av deras respektive koordinater, och om dessa är proportionella mot varandra kommer vektorerna att vara kollinära. Detta uttrycks enligt följande:

Kan tjäna dig: motsvarande uppsättningar: vad är, förklaring, exempel

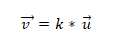
Exempel 1

Du har vektorer A = (10, 5) och B = (6, 3). För att avgöra om de är colineal tillämpas den bestämmande teorin, som fastställer jämställdhet mellan tvärprodukter. På detta sätt måste du:

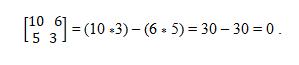
Colineal vektorsystem

Colineala vektorer representeras grafiskt med hjälp av riktningen och riktningen för dessa - med tanke på att dessa måste gå igenom applikationspunkten - och modulen, som är en specifik skala eller längd.

Colineal vektorsystem bildas när två eller flera vektorer verkar på ett objekt eller en kropp, som representerar en kraft och verkar i samma riktning.

Till exempel, om två kolineala krafter appliceras på en kropp, kommer den resulterande en av dessa bara att bero på känslan som de agerar. Det finns tre fall som är:

Colineala vektorer med motsatta sinnen

Resultatet av två kolinala vektorer är lika med summan av dessa:

R = ∑ f = f₁ + F_2.

Exempel

Om två F -styrkor verkar på en vagn₁ = 40 n och f₂ = 20 n i motsatt riktning (som visas på bilden) är resultatet:

R = ∑ f = (- 40 n) + 20n.

R = - 20 n.

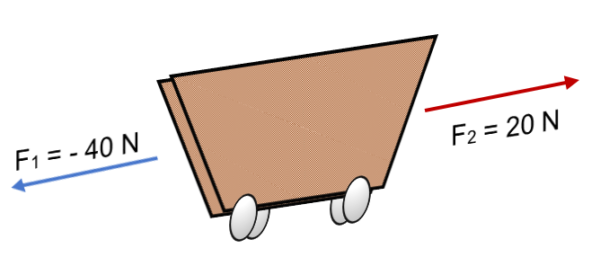Det negativa tecknet uttrycker att kroppen kommer att röra sig till vänster, med en kraft motsvarande 20 n.

Colineala vektorer i samma mening

Storleken på den resulterande kraften kommer att vara lika med summan av de kolineala vektorerna:

R = ∑ f = f₁ + F_2.

Exempel

Om två F -styrkor verkar på en vagn₁ = 35 n och f₂ = 55 n i samma riktning (som visas på bilden) är resultatet:

R = ∑ f = 35 n + 55n.

R = 90 n.

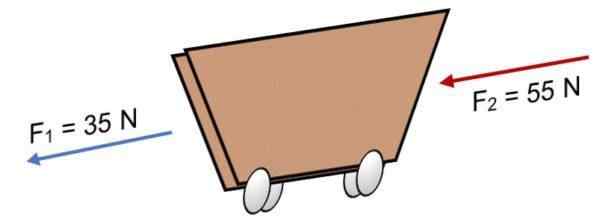
Det positiva resultatet indikerar att kollineala vektorerna verkar till vänster.

Det kan tjäna dig: regel t: egenskaper, så att det är exempel

Colineala vektorer med lika storheter och motsatta sinnen

Resultatet av de två kollineala vektorerna kommer att vara lika med summan av de kollinära vektorerna:

R = ∑ f = f₁ + F_2.

Eftersom krafterna har samma storlek men i motsatt riktning -det vill säga att en kommer att vara positiv och en annan negativ -genom att lägga till de två krafterna kommer resultatet att vara lika med noll.

Exempel

Om två F -styrkor verkar på en vagn₁ = -7 n och f₂ = 7 n, som har samma storlek, men i motsatt riktning (som visas på bilden) är resultatet:

R = ∑ f = (-7 n) + 7n.

R = 0.

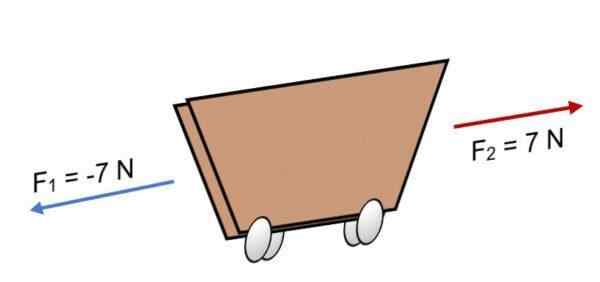
Eftersom resultatet är lika med 0, betyder det att vektorer balanserar med varandra och därför är kroppen i balans eller vila (den kommer inte att röra sig).

Skillnaden mellan colineal och samtidiga vektorer

Colineal vektorer kännetecknas av att ha samma riktning på samma linje, eller för att de är parallella med en linje; Det vill säga de är parallella linjedirektörer vektorer.

För sin del definieras samtidiga vektorer eftersom de befinner sig i olika handlingslinjer som avlyssnas vid en enda punkt.

Med andra ord har de samma ursprungspunkt eller ankomst -oavsett sin modul, vilket betyder eller riktar en vinkel mellan dem.

Samtidiga vektorsystem löses med matematiska eller grafiska metoder, som är parallellogrammetoden för krafter och metod för kraftpolygonen. Genom dessa kommer värdet på en resulterande vektor att bestämmas, vilket indikerar riktningen i vilken en kropp kommer att röra sig.

I grund och botten är den största skillnaden mellan de kollinära och samtidiga vektorerna handlingslinjen där de agerar: kollinealerna agerar i samma linje, medan de samtidiga i olika.

Kan tjäna dig: System med ekvationer: Lösningsmetoder, exempel, övningar

Det vill säga, de kollinära vektorerna agerar i ett enda plan, "x" eller "y"; Och den samtidiga handlingen i båda planen, från samma punkt.

Colineal vektorer är inte vid en tidpunkt, som de samtidiga gör, eftersom de är parallella med varandra.

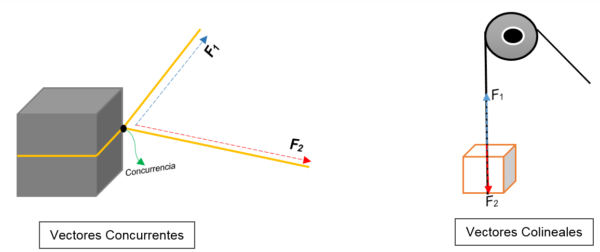
I den vänstra bilden kan du se ett block. Den är bunden med ett rep och knuten delar upp det i två; När blocket hittas mot olika orienteringar och med olika krafter kommer blocket att gå mot samma riktning.

Två vektorer representeras vid en punkt (blocket), oavsett deras modul, riktning eller riktning.

Å andra sidan, i rätt bild verkar en remskiva som lyfter en låda. Repet representerar handlingslinjen; När det stoppas agerar två krafter (vektorer) på det: en spänningskraft (när du klättrar i blocket) och en annan kraft, som utövar blockets vikt. Båda har samma riktning, men i motsatta sinnen; De håller inte med på en punkt.