Equipocent Vectors Definition, Notation, Ovess

Två eller flera Vektorer är utrustning Om de har samma modul, samma riktning och lika känsla, även när deras ursprungspunkt är annorlunda. Kom ihåg att egenskaperna hos en vektor är exakt: ursprung, modul, riktning och känsla. 

Vektorer representeras av ett orienterat eller pilsegment. Figur 1 visar representationen av flera vektorer i planet, av vilka några är utrustning enligt definitionen som ursprungligen gavs.

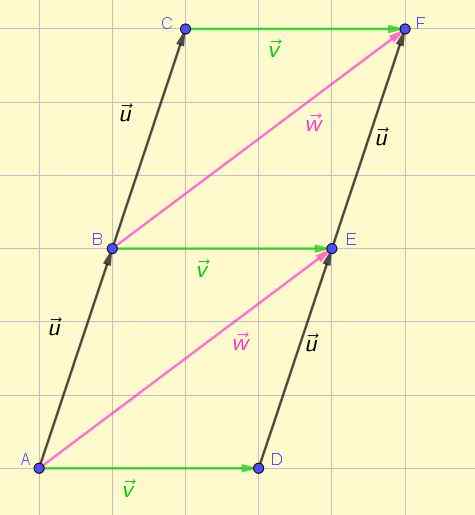Figur 1. Utrustning och icke -utrustningsvektorer. Källa: Självgjord.

Från en första anblick är det möjligt att uppskatta att de tre gröna vektorerna har samma storlek, samma riktning och samma känsla. Detsamma kan bekräftas om de två rosa vektorerna och de fyra svarta vektorerna.

Många naturstorlekar har ett vektorbeteende, så är fallet med hastighet, acceleration och styrka, för att bara nämna några. Därför vikten av att ordentligt karakterisera dem.

[TOC]

Notation för vektorer och utrustning

För att skilja vektormängderna för de skalära mängderna, används det svarta brevet eller en pil på bokstaven ofta. När du arbetar med handvektorer, på anteckningsboken, är det nödvändigt att skilja dem med pilen och när ett tryckt medium används används djärva.

Vektorer kan nekas, vilket indikerar deras utgångspunkt eller ursprung och deras ankomstpunkt. Till exempel Ab, före Kristus, AV och Ef i figur 1 är dock vektorer Ab, före Kristus, AV och Ef De är skalära mängder eller siffror som anger storleken, modulen eller storleken på deras respektive vektorer.

För att indikera att två vektorer är utrustning används symbolen "∼ ". Med denna notation kan vi i figuren påpeka följande vektorer som är utrustning med varandra:

Kan tjäna dig: Kinetisk energi: Egenskaper, typer, exempel, övningar

AB∼Bc∼de 

De har alla samma storlek, riktning och mening. Följ därför de regler som anges ovan.

Gratis, glidande och motsatta vektorer

Någon av vektorerna i figuren (till exempel Ab) är en representant för uppsättningen av alla fasta vektorer. Denna oändliga uppsättning definierar klassen med fria vektorer eller.

eller = AB, BC, från, EF, ..

En alternativ notation är som följer:

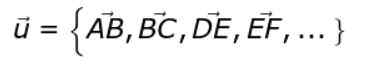
Om den djärva eller pilen inte är placerad på toppen eller, Vi vill hänvisa till vektormodulen eller.

Fria vektorer appliceras inte på någon speciell punkt.

För sin del Glidvektorer De är utrustning utrustning till en given vektor, men deras appliceringspunkt måste finnas i vektoråtgärdslinjen.

Och den motsatta vektorer De är vektorer som har samma storlek och riktning men motsatta sinnen, även om de i engelska texter kallas motsatta adresser Eftersom adressen också anger innebörden. Motsatta vektorer är inte utrustning.

Övningar

-Övning 1

Vilka andra vektorer av de som visas i figur 1 är utrustning med varandra?

Lösning

Bortsett från de som redan anges i föregående avsnitt observeras det från figur 1 att Annons, Vara och Ec De är också ekvipocentvektorer med varandra:

AD ∼ vara ∼ ce 

Någon av dem är en representant för klassen med fria vektorer v.

Vektorer är också utrustning Ae och Bf :

Ae ∼ Bf 

Som är klassrepresentanter W.

-Övning 2

Poäng A, B och C är på Cartesian XY -plan och deras koordinater är:

Kan tjäna dig: idealisk gas: modell, beteende, exempel

A = (-4.1), B = (-1.4) och C = (-4, -3)

Hitta koordinaterna för en fjärde punkt D så att vektorerna Ab och CD Vara utrustning.

Lösning 

Så att CD vara utrustning Ab måste ha samma modul och samma riktning som Ab .

Modulen av Ab Kvadrat är:

|Ab|^2 = (-1 -( -4))^2 + (4 -1)^2 = 9 + 9 = 18

D Koordinater är okända för vad vi kan säga: D = (X, Y)

Sedan: |CD|^2 = (x -(-4))^2 + (y -( -3))^2

Som |Ab| = |CD| Det är ett av villkoren för Ab och CD Vara utrustning du har:

(x + 4)^2 + (y + 3)^2 = 18

Eftersom det finns två okända krävs en annan ekvation, vilket kan uppnås utifrån det villkor Ab och CD vara parallell och i samma mening.

Vektor AB -sluttning

Vektorlutningen Ab Anger din adress:

I väntan på AB = (4 -1)/(-1 -( -4)) = 3/3 = 1

Indikerar att vektorn Ab 45º -form med X -axeln.

Cd vektor lutning

Lutningen av CD Det beräknas på liknande sätt:

Väntande cd = (y -( -3))/(x -(-4)) = (y + 3)/(x + 4)

Matchar detta resultat med lutningen av Ab Du har följande ekvation:

Y + 3 = x + 4 

Vilket betyder y = x + 1.

Om detta resultat ersätts i ekvationen av jämställdhet mellan modulerna, är det:

(x + 4)^2 + (x + 1 + 3)^2 = 18

Förenklande är:

2 (x+4)^2 = 18, 

Vilket motsvarar:

(x+4)^2 = 9

Det är x+4 = 3 vilket innebär att x = -1. Så att koordinaterna för D är (-1, 0).

kolla upp

Vektorkomponenter Ab De är (-1-(-4); 4 -1) = (3; 3)

Kan tjäna dig: Thévenin Theorem: Vad består, applikationer och exempel

och vektorns vektor CD De är (-1-(-4)); 0 -(-3)) = (3; 3)

Vilket innebär att vektorer är utrustning. Om två vektorer har samma kartesiska komponenter har samma modul och riktning, är de därför utrustning.

-Övning 3

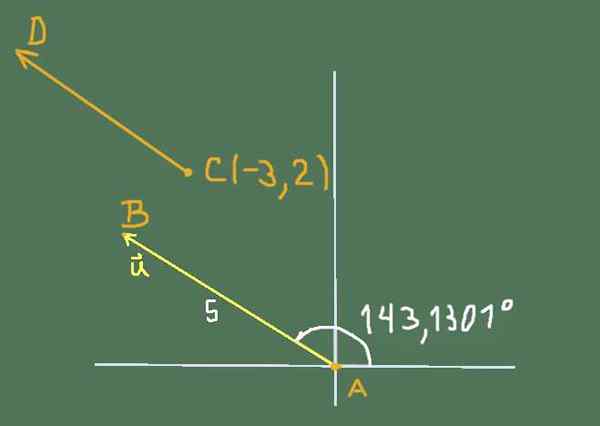
Den fria vektorn eller har storlek 5 och adress 143,1301º.

Hitta dess kartesiska komponenter och bestäm koordinaterna för punkterna B och C och vet att fasta vektorer AB och CD är utrustning. Koordinaterna för A är (0, 0) och koordinaterna för punkt C är (-3,2).

Lösning 

Den situation som föreslås av övningen kan representeras av följande figur:

figur 2. Diagram för upplösning av övning 3. Källa: Självgjord.

Kartesiska komponenter av eller are

eller = (5*cos (143,1301º); 5*sin (143,1301º)) 

Att göra beräkningarna kvarstår:

eller = (-4; 3) 

B -koordinater är okända, så vi kommer att placera B (X, Y)

Vektors koordinater Ab De är (X-0; Y-0), men eftersom det är utrustning med U måste uppfyllas jämställdhet mellan komponenter, dras därför slutsatsen att koordinaterna för B är (-4, 3).

På liknande sätt koordinaterna CD De är (x-(-3)); (och - 2) Det måste vara utrustning u, leller det leder till:

 x + 3 = -4 och y -2 = 3

Då kommer koordinaterna för punkt D att vara (-7, 5).

Referenser

1. Beräkning.Likström. Fast vektor. Fri vektor. Återhämtad från: beräkning.Likström
2. 2d Descartes. Fasta vektorer och fria vektorer i planet. Hämtad från: resurser.utbildning.är
3. Guao -projekt. Ekvektor. Återhämtat sig från: guao.org
4. Resnick, r., Kran, k. (2001). Fysik (på engelska). New York: John Wiley & Sons.
5. Serway, R.; Jewett, John W. (2004). Fysik för forskare och ingenjörer (på engelska) (6: e upplagan). Brooks/Cole.
6. Tupler, Paul a. (2000). Fysik för vetenskap och teknik. Volym I. Barcelona: Ed. Jag reverserade.
7. Weisstein, E. "Vektor". I Weisstein, Eric W. Mathworld (på engelska). Wolfram Research.