Areolär hastighet hur det beräknas och lösta övningar

De Areolär hastighet Det är det svepande området per tidsenhet och är konstant. Det är typiskt för varje planet och uppstår från beskrivningen av Keplers andra lag på matematiskt sätt. I den här artikeln kommer vi att förklara vad den består av och hur den beräknas.

Bommen som representerar upptäckten av planeter utanför solsystemet har återaktiverat intresset för planetörelsen. Ingenting tror att dessa exo-planer följer andra lagar än de som redan är kända och giltiga för solsystemet: Keplers lagar.

Johannes Kepler var astronomen som, utan hjälp av teleskopet och använde observationerna från hans mentor Tycho Brahe, skapade en matematisk modell som beskriver rörelsen av planeterna runt solen.

Han lämnade denna modell uttryckt i de tre lagarna som bär hans namn och som förblir lika giltigt idag som 1609, när han etablerade de första två och 1618, datum då det tredje.

[TOC]

Kepler lagar

På nuvarande språk säger Keplers tre lagar så här:

1. Banorna för alla planeter är elliptiska och solen är i fokus.

2. Positionsvektorn som går från solen till en planet sveper lika områden i lika tider.

3. Kvadratet på en planets omloppsperiod är proportionell mot kuben för den beskrivna halvkönen.

En planet kommer att ha en linjär hastighet, som alla kända objekt som rör sig. Och det finns mer: När man skriver Keplers andra lag i matematisk form uppstår ett nytt koncept som heter Aesolar Speed, typiskt för varje planet.

Varför rör sig planeter elliptiskt runt solen?

Jorden och de andra planeterna rör sig runt solen tack vare det faktum att den utövar en kraft på dem: Gravitationsvatten. Detsamma gäller för alla andra stjärna och planeterna som överensstämmer med ditt system, om du har dem.

Det kan tjäna dig: känslig värme: koncept, formler och övningar löst

Detta är en kraft av den typ som kallas Central Force. Vikten är en central kraft som alla är bekanta. Objektet som utövar den centrala kraften, vare sig det är solen eller en avlägsen stjärna, lockar planeterna mot deras centrum och de rör sig och beskriver en stängd kurva.

I princip kan denna kurva approximeras som en omkrets, som Nicolás Copernico, en polsk astronomskapare av den heliocentriska teorin, gjorde.

Ansvarig kraft är gravitationsattraktion. Denna kraft beror direkt på massorna på stjärnan och planeten i fråga och är omvänt proportionell mot kvadratet på avståndet som skiljer dem.

Problemet är inte så enkelt, för i ett solsystem interagerar alla element på detta sätt och lägger till komplexiteten i saken. De är inte heller partiklar, eftersom stjärnor och planeter är mätbara storlek.

Av denna anledning är den centrala punkten i bana eller krets som reste av planeterna inte exakt centrerad på stjärnan, men på en punkt känd som tyngdpunkten i solplanet-systemet.

Den resulterande bana är elliptisk. Följande bild visar den och tar som ett exempel jorden och solen:

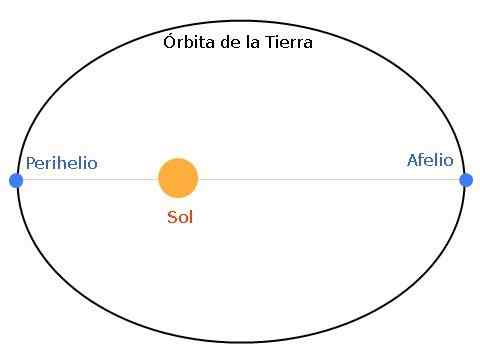Figur 1. Jordens bana är elliptisk, med solen belägen i en av focierna. När jorden och solen är på sitt maximala avstånd sägs det att jorden är i afelium. Och om avståndet är minimalt pratar vi om perihelio.

Apeliet är den längsta positionen från jorden till solen, medan periheliet är den närmaste punkten. Ellipsen kan mer eller mindre plattas, enligt stjärnsystemets egenskaper - planet.

Asels och perihelio -värden varierar årligen, eftersom de andra planeterna orsakar störningar. För andra planeter kallas dessa positioner stöd respektive expertis.

Storleken på en planets linjära hastighet är inte konstant

Kepler upptäckte att när en planet kretsar runt solen, under sin Barr -rörelse lika områden i lika tider. Figur 2 visar grafiskt innebörden av detta:

Det kan tjäna dig: vad är partikelns balans? (Med exempel)figur 2. Planetens positionsvektor med avseende på solen är r. När planeten beskriver sin bana reser en ellipsbåge i en tid ΔT.

Matematiskt det faktum att₁ vara lika med₂ Det uttrycks så här:

Bågarna är små, så att varje område kan närma sig en triangel:

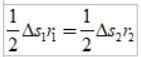
Som ΔS =vΔt, Där v är planetens linjära hastighet vid en given punkt, när vi ersätter har vi:

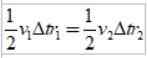
Och eftersom tidsintervallet är detsamma, erhålls det:

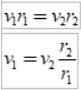
Som r₂ > r₁, sedan v₁ > v₂, Med andra ord är den linjära hastigheten på en planet inte konstant. Faktum är att jorden går snabbare när den är i perihelium än när den är i aphelium.

Därför är jordens linjära hastighet eller någon planet runt solen inte en storlek som tjänar till att karakterisera den nämnda planetens rörelse.

Areolär hastighet

Keplers andra lag tyder på en ny storlek som kallas areolär hastighet. Det definieras som området svepte per tidsenhet och är konstant. För att beräkna det används följande figur:

Figur 3. Jordens positionsvektor (eller planet) med avseende på solen är R, och när man rör sig upplever jorden en förskjutning, även vektor ΔR.

Ett litet område som sveps av jorden väljs när vi utför sin elliptiska krets, som vi kommer att beteckna hur ΔA. Den tid som behövs för detta är Δt.

Figur 3 visar jordens positionsvektor med avseende på solen, betecknad med r. När jorden rör sig, upplev en förskjutning ΔR.

Detta område motsvarar hälften av rektangelområdet som visas i figur 3:

Kvoten ΔR/ΔT är just jordens linjära hastighet, så den areolära hastigheten kvarstår:

V_TILL I det internationella systemet är de:

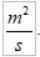
Observera att medan både R och V varierar förblir produkten konstant. Detta förvandlar isolära hastighet till en mycket lämplig storlek för att karakterisera rörelsen på en planet runt dess stjärna.

Kan tjäna dig: Antoinkonstanter: Formler, ekvationer, exempel

Produkten av R och V är storleken på vinkelmomentet L, så att den areolära hastigheten kan uttryckas som:

Beräkning av linjär hastighet och isolär hastighet

Med följande exempel kommer vi att visa hur man beräknar den areolära hastigheten när vissa parametrar för planetrörelsen är kända:

Träning

En exo-planet rör sig runt sin sol efter en elliptisk bana, enligt Keplers lagar. När det är i Expertro är dess radiovektor R₁ = 4 · 10⁷ km, och när det är i stödet är r₂ = 15 · 10⁷ km. Den linjära hastigheten i sin expertis är v₁ = 1000 km/s.

Beräkna:

A) Hastighetens storlek i stödet.

B) exo-planens areolära hastighet.

C) Längden på ellipsen major semi -axeln.

Svara på)

Ekvationen används:

där numeriska värden byts ut.

Varje term identifieras enligt följande:

v₁ = Hastighet i stöd; v₂ = Hastighet hos experten; r₁= Författaravstånd,

r₂= Avstånd från experten.

Med dessa värden erhålls det:

Svar B)

Ekvationen som ska användas är

där paret av värden r och v för Expertro eller stödet kan bytas ut, eftersom v_TILL Det är en planetkonstant:

Svar C)

Längden på den stora semi -axeln av ellipsen är semi -semi -semi -semi -semi -seismum och expertis:

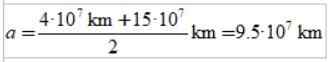
Bibliografi

1. Serway, R., Jewett, J. (2008). Fysik för vetenskap och teknik. Volym 1. Mexiko. Cengage Learning Editors. 367-372.
2. Akter, D. (2005). De tre Kepler -lagarna i planetrörelsen. Hämtad från PWG.Gsfc.pott.Gov
3. Obs: Den föreslagna övningen togs och modifierades från följande text i en McGrawhill -bok. Tyvärr är det ett isolerat kapitel i PDF -format, utan titeln eller författaren: mheducation.Es/bcv/guide/kapitel/844817027x.Pdf