Relativ hastighetskoncept, exempel, övningar

De Relativ hastighet av ett objekt är ett som mäts med avseende på en given observatör, eftersom en annan observatör kan få ett annat mått. Hastigheten beror alltid på observatören som mäter den.

Därför kommer hastigheten för ett objekt mätt av en viss person att vara den relativa hastigheten med avseende på den. En annan observatör kan få ett annat värde för hastigheten, fortfarande i fallet med samma objekt.

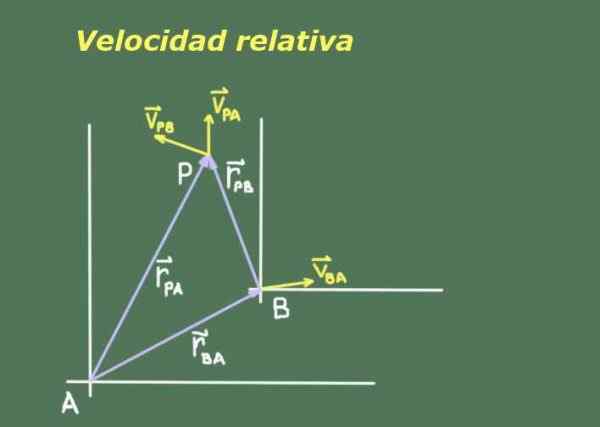
Figur 1. Schema som representerar till punkten P i rörelse, sett från referenssystem A och B. Källa: Självgjord.

Som två observatörer A och B som rör sig från varandra kan de ha olika mått på ett tredje P -objekt som rör sig, det är nödvändigt att leta efter en relation mellan positionerna och hastigheterna för P -vyer av A och B.

Figur 1 visar två observatörer A och B med sina respektive referenssystem, från vilka de mäter positionen och hastigheten på objektet P.

Varje observatör A och B mäter positionen och hastigheten för objekt P vid en viss tidpunkt t. I klassisk relativitet (eller galileisk) är tiden för observatör A densamma som för observatör B oavsett dess relativa hastigheter.

Den här artikeln handlar om klassisk relativitet som är giltig och tillämplig i de flesta vardagliga situationer där föremål har mycket lägre hastigheter än ljuset.

Observatörens B: r_Ba. Eftersom positionen är en vektorbelopp använder vi djärva för att ange det. Objektets P: s position med avseende på en betecknar som r_Pa och det för samma objekt P angående B r_Pb.

[TOC]

Förhållandet mellan positioner och relativa hastigheter

Det finns ett vektorförhållande mellan dessa tre positioner som kan härledas från representationen av figur 1:

 r_Pa= r_Pb + r_Ba

Om det tidigare uttrycket tas med avseende på tid t Vi kommer att få förhållandet mellan de relativa hastigheterna för varje observatör:

Du kan tjäna dig: Newtons andra lag: applikationer, experiment och övningar

V_Pa= V_Pb + V_Ba

I det föregående uttrycket finns det den relativa hastigheten för P med avseende på en beroende på den relativa hastigheten för P med avseende på B och den relativa hastigheten för B med avseende på.

På liknande sätt kan den relativa hastigheten för P skrivas med avseende på den relativa hastigheten för P med avseende på A och den relativa hastigheten på B.

V_Pb= V_Pa + V_Ab

Det bör noteras att den relativa hastigheten för B är lika och strider mot B med avseende på A:

V_Ab = -V_Ba 

Detta ses av ett barn från en rörlig bil

En bil går en rak väg, som går från väster till detta, snabbt från 80 km/h medan den är i motsatt riktning (och på den andra körfältet) kommer en motorcykel snabbt 100 km/h.

I baksätet på bilen reser ett barn som vill veta den relativa hastigheten på en motorcykel som närmar sig honom. För att ta reda på svaret kommer barnet att tillämpa de relationer du just har läst i föregående avsnitt och identifiera varje koordinatsystem enligt följande:

-A är koordinatsystemet för en observatör på vägen och med avseende på det har rapiderna för varje fordon uppmättts.

-B är bilen och P kommer att vara motorcykeln.

Om du vill beräkna hastigheten på moto p med avseende på bil B kommer följande förhållande att tillämpas:

V_Pb= V_Pa + V_Ab=V_Pa - V_Ba

Tar som positivt den västra östriktningen du har:

V_Pb= (-100 km/h - 80 km/h) Yo = -180 km/h Yo

Detta resultat tolkas på följande sätt: Motorcykeln rör sig med avseende på bilen med en hastighet av 180 km/h och riktning -Yo, det vill säga detta till väst.

Det kan tjäna dig: Block Algebra: Elements, Exempel, Löst övningar

Relativ hastighet mellan motorcykeln och bilen

Motorcykeln och bilen har korsat var och en efter deras körfält. Pojken som går i baksätet på bilen ser motorcykeln och nu vill veta med vilken hastighet han flyttar bort från honom, förutsatt att både motorcykel och bil upprätthåller samma rapider som före korsningen.

För att veta svaret tillämpar barnet samma relation som tidigare användes:

V_Pb= V_Pa + V_Ab=V _Pa - V_Ba

V_Pb= -100 km/h Yo - 80 km/h Yo = -180 km/h Yo

Och nu rör sig motorcykeln bort från bilen med samma relativa hastighet som de närmade sig innan de korsade.

Samma motorcykel av del 2 avkastning genom att hålla samma hastighet på 100 km/h men ändra sin adress. Det vill säga bilen (som fortsätter snabbt 80 km/h) och motorcykeln rör sig båda i en positiv riktning.

Vid en tidpunkt överskrider motorcykeln bilen, och barnet som går i bilens baksäte vill veta den relativa hastigheten på motorcykeln med avseende på honom när han ser henne passera hennes sida.

För att få svaret tillämpar barnet igen relationerna från den relativa rörelsen:

V_Pb= V_Pa + V_Ab=V_Pa - V_Ba

V_Pb= +100 km/h Yo - 80 km/h Yo = 20 km/h Yo 

Barnet från baksätet observerar motorcykeln som främjar bilen med en hastighet på 20 km/h.

-Träning löst

Övning 1

En motorbåt korsar en flod på 600 m bred och flyter från norr till söder. Flodens hastighet är 3 m/s. Båthastigheten med avseende på flodvattnet är 4 m/s i öster.

Kan tjäna dig: grenar av klassisk och modern fysik

(i) Hitta båthastigheten med avseende på flodstranden.

(ii) Ange båtens hastighet och riktning med avseende på mark.

(iii) Beräkna korsningstiden.

(iv) Hur mycket kommer att ha rört sig söderut med avseende på utgångspunkten.

Lösning 

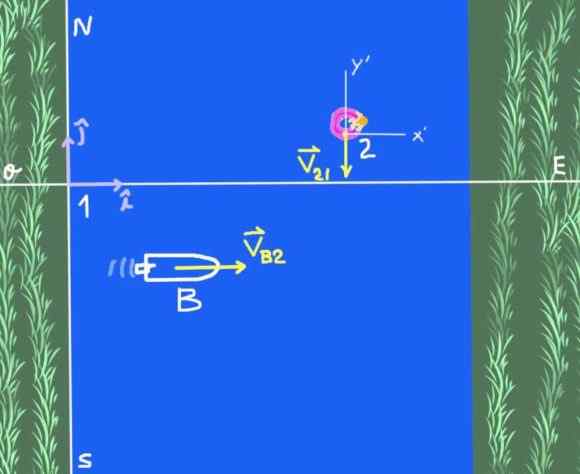figur 2. Båt som korsar floden (övning 1). Källa: Självgjord.

Det finns två referenssystem: Solidaritetsreferenssystemet vid flodstranden som vi kommer att kalla 1 och referenssystemet 2 som är en observatör som flyter på flodvattnet. Syftet med studien är båt B.

Båtens hastighet med avseende på floden är skriven i en vektorform enligt följande:

VB2 = 4 Yo Fröken

Hastigheten på observatören 2 (flotte över floden) med avseende på observatör 1 (på land):

Vtjugoett = -3 J Fröken

Du vill hitta båthastigheten med avseende på mark VB1.

VB1 = VB2 + Vtjugoett

Svar i

VB1 = (4 Yo - 3 J) Fröken   

Båtens hastighet är den tidigare hastighetsmodulen:

|VB1| = (42 + (-3) 2) ½ = 5 m/s

Svar II

Och adressen kommer att vara:

θ = arcan (-¾) = -36,87º 

Svar III

Båtens korsningstid är förhållandet mellan flodens bredd och komponenten X på båthastigheten med avseende på jorden.

t = (600 m)/(4 m/s) = 150 s 

SVAR IV

För att beräkna den drift som båten hade till söder, multipliceras komponenten och hastigheten på båten med avseende på marken med korsningstiden:

d = -3 J m/s * 150 s = -450 J m

Förskjutningen i söder med avseende på utgångspunkten är 450 m.

Referenser

1. Giancoli, D. Fysik. Principer med applikationer. Sjätte upplagan. Prentice hall. 80-90
2. Resnick, r. (1999). Fysisk. Volym 1. Tredje upplagan på spanska. Mexiko. Kontinentala redaktionella företag s.TILL. av C.V. 100-120.
3. Serway, R., Jewett, J. (2008). Fysik för vetenskap och teknik. Volym 1. 7th. Utgåva. Mexiko. Cengage Learning Editors. 95-100.
4. Wikipedia. Relativ hastighet. Återhämtat sig från: Wikipedia.com
5. Wikipedia. Relativ hastighetsmetod. Återhämtat sig från: Wikipedia.com