Icke -koplanära vektorer definition, förhållanden, övningar

De Icke -koplanarvektorer De är de som inte delar samma plan. Två fria vektorer och en punkt definierar ett enda plan. En tredje vektor kan eller inte dela det planet och om det inte gör det är det icke -koplanära vektorer.

Icke -kopparvektorer kan inte representeras i två dimensionella utrymmen som ett bräde eller ett pappersark, eftersom några av dem finns i den tredje dimensionen. För att representera dem ordentligt måste du använda perspektiv.

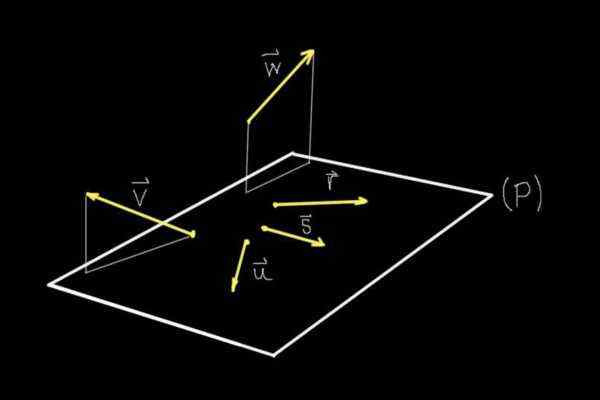Figur 1. Coplanares och icke-kopplingsvektorer. (Egen utarbetande)

Om vi ​​observerar figur 1 är alla objekt som strikt visas i skärmens plan, men tack vare det perspektiv kan vår hjärna föreställa sig ett plan (P) som kommer ut av samma.

På det planet (P) finns vektorerna r, s, eller, Medan vektorer v och W  De är inte på det planet.

Därför vektorerna r, s, eller De är Coplanarios eller Coplanares med varandra eftersom de delar samma plan (P). Vektorerna v och W De delar inte en lägenhet med någon av de andra vektorerna som visas, därför är de icke-koppling. 

[TOC]

Coplanares och planekvationsvektorer

Ett plan är unikt definierat om tre punkter ges i det tre dimensionella utrymmet.

Anta att dessa tre punkter är poängen TILL, punkt B och poängen C som definierar planet (P). Med dessa punkter är det möjligt att bygga två vektorer AB = U och Ac = v som är genom konstruktion med planet (P).

Vektorn (eller tvärprodukten) produkten av dessa två vektorer resulterar i en tredje vinkelrätt (eller normal) vektor för dem och därför vinkelrätt mot planet (P):

n = u X v   => n ⊥ eller  och n ⊥ v   => n ⊥ (P)    

Kan tjäna dig: vikt (fysisk): beräkning, enheter, exempel, övningar

Någon annan punkt som tillhör planet (P) måste uppfylla att vektorn Aq vara vinkelrätt mot vektorn n; Detta motsvarar att säga att den skalära produkten (eller punktprodukten) av n med Aq Det måste vara noll:

n • Aq = 0 (*)

Det föregående villkoret motsvarar att säga att:

Aq • (eller X v) = 0 

Denna ekvation säkerställer att punkten Q tillhör planet (P). 

Cartesian Equation of the Plane

Den föregående ekvationen kan skrivas på kartesiskt sätt. För detta skriver vi koordinaterna för punkterna TILL, Q och komponenterna i den normala vektorn n:

A = (A, B, C)

Q = (x, y, z)

n= (NX, NY, NZ)

Så att AQ -komponenterna är:

Aq= (X-a, y-b, z-c)

Villkoret för vektorn Aq vara inne i planet (P) Det är villkoret (*) som nu är skrivet så här:

(NX, NY, NZ) • (X-A, Y-B, Z-C) = 0

Beräkning av punktprodukten återstår:

nx (x-a) + ny (y-b) + nz (z-b) = 0

Om det utvecklas och ordnar om det kvarstår:

nx x + ny y + nz z = nx a + ny b + nz c

Det föregående uttrycket är den kartesiska ekvationen i ett plan (P), beroende på komponenterna i en normal vektor till (P) och koordinaterna för en punkt TILL som tillhör (P).

Förhållandena för att tre vektorer ska vara icke -koplanarer

Som villkoret har sett i föregående avsnitt Aq • (eller X v) = 0 garanterar att vektorn Aq Det är Coplanario a eller och v.

Om vi ​​ringer W till vektorn Aq Då kan vi bekräfta det:

W, eller och v De är Coplanares, ja och bara om W • ( eller X v ) = 0.

Villkor för icke-beteende

Om trippelprodukten (eller blandad produkt) från tre vektorer skiljer sig från noll är de tre vektorerna icke-täckningar.

Det kan tjäna dig: Politropic Process: Egenskaper, applikationer och exempel

Ja    W • ( eller X v ) ≠ 0 Då är U-, V- och W-vektorerna icke-colutarios.

Om de kartesiska komponenterna i U, V, V och W introduceras kan villkoret för icke-beteende skrivas enligt följande:

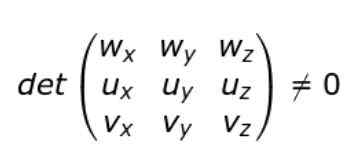Det vill säga att om determinanten för matrisen (3 × 3) vars rader är komponenterna i U, V och W-vektorerna så är vektorerna icke-koppling.

Trippelprodukten har en geometrisk tolkning och representerar volymen av den parallellepiped som genereras av de tre icke -koplanarvektorerna.

figur 2. Tre icke-kopplingsvektorer definierar en parallellepipedo vars volym är trippelproduktmodulen. (Egen utarbetande)

Anledningen är som följer; När två av icke-kopplingsvektorerna multiplicerar. 

Sedan när denna vektor multiplicerar. 

Med andra ord har du det parallellogramområdet som genereras av de två första multiplicerade med höjden på den tredje vektorn.

Alternativt tillstånd för icke-koppling

Om du har tre vektorer och någon av dem inte kan skrivas som en linjär kombination av de andra två, är de tre vektorerna icke-täckningar. Det är tre vektorer eller, v och W De är icke-täckningar om tillståndet:

a eller + p v + y W = 0

Det uppfylls endast när α = 0, β = 0 och y = 0.

Löst övningar

-Övning 1

Du har tre vektorer

eller = (-3, -6, 2);   v = (4, 1, 0) och W = (-1, 2, z)

Observera att vektorns Z -komponent W Det är okänt.

Hitta värdena som Z kan ta så att det är garanterat att de tre vektorerna inte delar samma plan.

Kan tjäna dig: stabil balans: koncept och exempel

Lösning 

Vi tillämpar återigen kriteriet för determinanten för matrisen som bildas av de tre vektors led, på detta sätt kvarstår vi: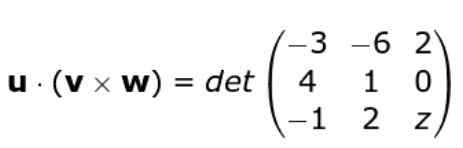Vi utvecklar determinanten

W • ( eller X v ) = -3 (z - 0) + 6 (4 z - 0) + 2 (8 + 1) = -3z + 24z + 18 = 21z + 18

Vi matchar detta uttryck till nollvärde

21 z + 18 = 0

Och vi rensar z

Z = -18/21 = -6/7

Om variabeln Z tog värdet -6/7 skulle de tre vektorerna vara coplanares.

Så att värdena på Z som garanterar att vektorerna är icke-täckningar är de som är i följande intervall:

Z ∈ (-(-6/7) u (-6/7, ∞)

-Övning 2

Hitta volymen på den parallellepiped som visas i följande figur:

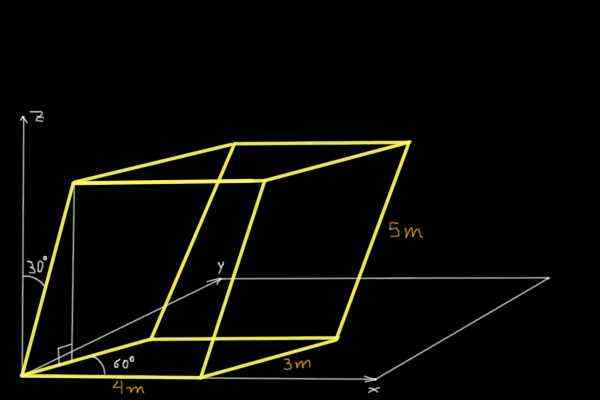
Lösning 

För att hitta volymen på den parallellepiped som visas i figuren kommer de kartesiska komponenterna i tre icke-sammanhängande icke-kopplingsvektorer att bestämmas i koordinatsystemets ursprung. Den första är vektorn eller  4m och parallellt med X -axeln:

eller= (4, 0, 0) m

Den andra är vektorn v I XY 3M -storleksplanet som bildar 60º med X -axeln:

v= (3*cos 60º, 3*Sen 60º, 0) = (1.5, 2.6, 0.0) m

Och den tredje vektorn W av 5 m och vars projektion i XY -planet bildas 60º med X -axeln, dessutom form 30º med Z -axeln.

W= (5*sin 30º*cos 60º, 5*SEN 30º*SIN 60º, 5*SEN 30º)

Genomförde de beräkningar vi har: W= (1.25, 2.17, 2.5 m.

Referenser

1. Figueroa, D. Serie: Physics for Science and Engineering. Volym 1. Kinematik. 31-68.
2. Fysisk. Modul 8: Vektorer. Återhämtat sig från: frtl.Utn.Edu.ar
3. Hibbeler, R. 2006. Mekanik för ingenjörer. Statisk. Sjätte upplagan. Continental Editor Company.28-66.
4. McLean, w. Schaumserie. Mekanik för ingenjörer: statisk och dynamisk. 3: e upplagan. McGraw Hill. 1-15.
5. Wikipedia. Vektor. Återhämtat sig från: det är.Wikipedia.org