Volym

Vi förklarar vad som är volymen, dess formler, enheter, hur man beräknar den och ger flera exempel

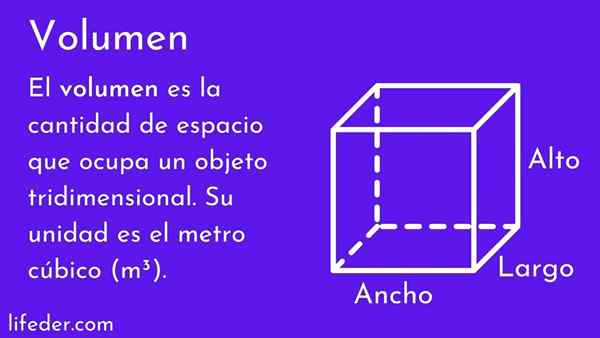
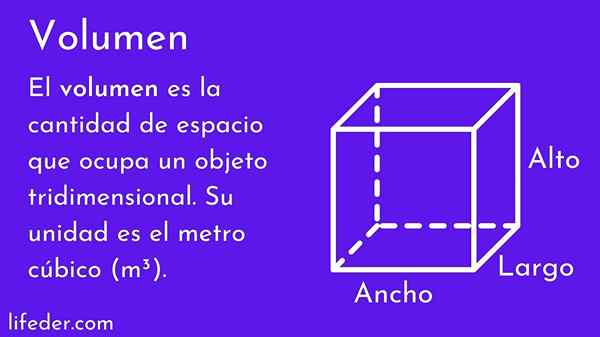
Vad är volymen?

han volym av en kropp är det numeriska värdet som mäter mängden utrymme. Den höga, bredd och djup bestämmer volymen, ju större, desto större är det ockuperade utrymmet.

Volymkonceptet är av stor betydelse, eftersom världen är tre dimensionell och alla föremål har bredd, höjd och djup, därför har de volym. Människor använder det ofta, till exempel genom att uppskatta om möblerna de vill köpa, passar den i sitt rum eller om de kommer in i en viss klänningsstorlek.

Inom vissa områden inom vetenskap och teknik, till exempel när man arbetar med vätskor, vare sig vätskor eller gaser, förvärvar den ockuperade volymen stor betydelse: när du fyller behållare och pumpar vätskor som vatten eller i utformningen av ett fartyg för ett fartyg för att se till Du sjunker inte. Allt detta gör det viktigt att bestämma det för många processer.

Det finns formler för att beräkna volymen av geometriska kroppar i regelbundna former, såsom prismor, sfärer, cylindrar och kottar, till exempel beroende på några av dess dimensioner. Och det finns också sätt att ta reda på volymen av oregelbundna objekt, vilket kommer att beskrivas lite senare.

Volymformler i geometriska figurer

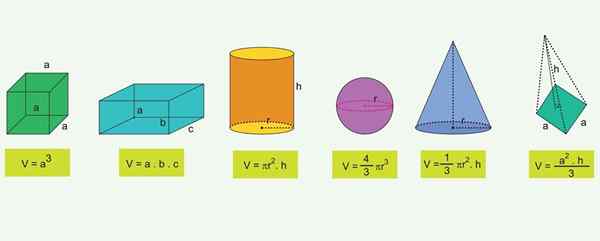Lista över de vanligaste geometriska figurerna och formeln för deras volymer

För de mest kända geometriska objekten finns formler som gör det möjligt att beräkna dess volym:

• Kub

V = ℓ³ 

Där v representerar volymen och ℓ är kanten (sidan) av kuben.

• Parallellepiped

En parallellepiped är en rektangulär låda med bredd "A", Long ℓ och "H" -höjden. Dess volym ges av produkten från dess tre dimensioner:

V = a ∙ ℓ ∙ h

• Sfär

Volymen på sfären beror på dess radie r:

Kan tjäna dig: Nicolás Copernico

• Rak cirkulär cylinder

Volymen på den raka cirkulära cylindern är produkten mellan dess bas och dess höjd "H". Eftersom basen är ett radioalbum “R”, vars område är a = π · r², Volymen kvarstår:

V = πr²∙ h

• Fitta

Konens volym är en tredjedel av produkten mellan området för den cirkulära basen A och höjden h. Som A = πr², så:

• Pyramid

För en pyramid vars basområde är en och har en höjd "H", ges volymen av:

Om pyramiden har en fyrkantig bas på sidan "A", som i figuren, är basområdet för basen att² Och pyramidens volym är:

V = (1/3) ⋅A²⋅H

• Prisma

Prismens volym är produkten mellan området A och höjden "H":

V = a ∙ h

Volymenheter

I det internationella enhetssystemet är enheten för volym kubikmätaren eller m³, Medan det är i Anglo -Saxon -systemet är det kubikfoten eller ft³ (av Fötter, som på engelska betyder "fot").

Det finns många andra enheter, beroende på storleken på det ockuperade utrymmet. Till exempel km kubikkilometer³ För större volymer eller kubikmillimeter mm³ För små volymer. Det finns också lokala användningsenheter.

Det är också nödvändigt att nämna kapacitetsenheterna, nära besläktade med volymen, som företrädesvis används för vätskor. Den centrala kapacitetsenheten är liter, förkortad L, vilket motsvarar en DM³ (Kubisk decimeter).

Andra enheter som är värda att nämna är gallon, den kubik tum, koppen och gikt, den senare brukade dosera mediciner.

Kan tjäna dig: jämförande metod

Hur mäts volymen?

Volymen på en kropp, som alla andra åtgärder, utförs jämfört med ett adekvat mönster, i detta fall en volymenhet.

Volymenheten definieras som kuben vars kant mäter 1 enhet. Denna enhet kan vara en mätare, centimeter, fot, tum eller någon annan. Sedan motsvarar objektets volym mängden kubiska enheter som är ockuperade av figuren och är alltid en positiv mängd.

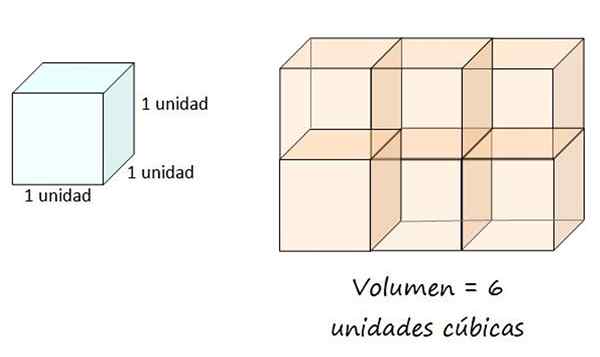En kubisk enhet definieras som volymen på en hink med kant lika med 1, så lådan till höger har en volym på 6 kubikenheter. Källa: f. Zapata.

Volym av en geometrisk kropp

När det gäller en geometrisk kropp som redan nämnts beräknas volymen genom lämplig formel, vilket mäter de dimensioner som indikeras av formeln.

Om du till exempel vill veta volymen på en sfär är det nödvändigt att mäta dess diameter och med den är dess radie känd, vilket är hälften. Om det är en rektangulär låda mäts bredden, höjden och djupet på samma.

Sedan sätts de värden som begärs i formeln in, se till att alla enheter är desamma, de nödvändiga operationerna utförs, det finns objektets volym.

Volym av en oregelbunden kropp

Oregelbundna fasta ämnen har inte en geometrisk form, till exempel en sten eller en blinkning. Trots detta kan du hitta dess volym med hjälp av en examen behållare full av vatten, med hjälp av vätskeflörningsmetoden.

För det första bestäms volymen som ockuperas av vattnet och då är det oregelbundna objektet helt nedsänkt, och mäter den nya volymen, som är större än originalet. Volymen på det oregelbundna objektet är skillnaden mellan denna volym och det för vattnet ensam.

Kan tjäna dig: Genie Wiley, den vilda flickan som bara kände igen hennes namn

För att denna metod ska fungera bör objektet inte göras av något ämne som lätt löses i vattnet, det måste förbli helt nedsänkt och naturligtvis måste du ha en examen behållare med nödvändig storlek för att rymma det helt.

Exempel

Den ungefärliga volymen för några kända objekt är:

• Jorden: 1.08321 × 10¹² km³
• Amazonas River: 225.000 m³/s (volymen per tidsenhet kallas "flöde")
• Gizas stora pyramid: 2.600.000 m³
• En fotboll: 5600 cm³
• En ryggsäck: 50 DM³

Volym och massa

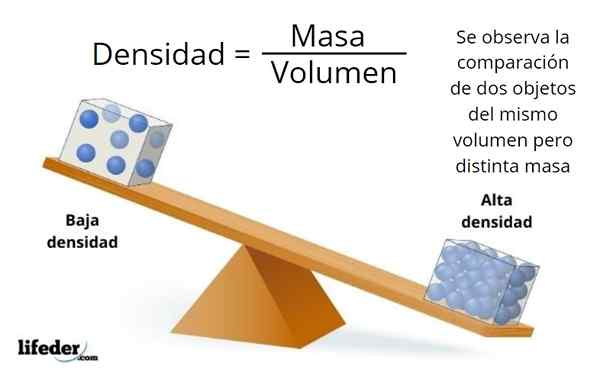
Volymen och massan är inte synonymer, den första är kopplad till objektets dimensioner och den andra till mängden materia som den innehåller.

Det kan finnas mycket materia i ett objekt med små dimensioner, eller väldigt lite i ett stort objekt, vilket beror på materialets densitet, vilket är förhållandet mellan massan och volymen på ett objekt:

Löst övningar

Övning 1

Beräkna volymen på en rektangulär låda vars dimensioner är 34 cm × 22 cm × 8 cm.

• Lösning

Volymen på en rektangulär låda är helt enkelt produkten från dess tre dimensioner:

V = 34 cm × 22 cm × 8 cm = 5984 cm³

Övning 2

Basen för en fyrkantig pyramid har ett område på 16 cm² Och dess höjd är 6 cm. Beräkna volymen av nämnda pyramid.

• Lösning

Formeln som anges ovan för volymen av en pyramid används, känt området för dess bas:

Och numeriska värden ersätts:

V = (1/3) × 16 cm² × 6 cm = 32 cm³