Centripetal Acceleration Definition, formler, beräkning, övningar

De centripetalacceleration till_c, Även kallad radiell eller normal, det är accelerationen som bär ett mobilt objekt när man beskriver en cirkulär bana. Hans storlek är v²/r, var r Det är cirkelns radie, den riktas mot mitten av den och ansvarar för att mobilen ska stanna kvar i sin rutt.

Måtten på centripetalacceleration är längd per enhetstid. I det internationella systemet är de m/s². Om Centripetal Acceleration av någon anledning försvinner, så gör också styrkan som tvingar mobilen att upprätthålla den cirkulära banan.

De roterande föremålen har centripetalacceleration, som är riktad mot banaens centrum. Källa: Pixabay

Det här är vad som händer med en bil som försöker ge en kurva på en platt och frostspår, där friktionen mellan golvet och hjulen är otillräcklig så att bilen tar kurvan. Därför är den enda möjligheten du har kvar att flytta i en rak linje och det är därför du kommer ut ur kurvan.

[TOC]

Cirkulära rörelser

När ett föremål rör sig i en cirkel är den centripetala acceleration hela tiden radiellt riktad mot mitten av omkretsen, riktning som är vinkelrätt mot den bana som följs följt.

Eftersom hastighet alltid är tangent till banan, så hastighet och centripetal acceleration visar sig vara vinkelrätt. Därför har hastighet och acceleration inte alltid samma riktning.

Under dessa omständigheter har mobilen möjlighet att beskriva omkretsen med konstant eller variabel hastighet. Det första fallet kallas enhetlig eller MCU -cirkulär rörelse av dess förkortning, det andra fallet kommer att vara en variabel cirkulär rörelse.

Det kan tjäna dig: vad är utsläppsavträdet? (Med exempel)

I båda fallen är Centripetal Acceleration ansvarig för att hålla den mobila cirklingen och ockuperar att hastigheten endast varierar i riktning och riktning.

För att ha en variabel cirkulär rörelse skulle dock en annan komponent i acceleration i samma hastighetsriktning vara nödvändig, vilket är ansvarigt för att öka eller minska hastigheten. Denna accelerationskomponent kallas Tangentiell acceleration.

Den variabla cirkulära rörelsen och den krökta rörelsen i allmänhet har båda komponenterna i accelerationen, eftersom den krökta rörelsen kan föreställa sig som vägen genom otaliga omkretsbågar som utgör den krökta banan.

Centripetalkraften

Nu är en styrka ansvarig för att tillhandahålla acceleration. För en satellit som kretsar runt jorden är det tyngdkraften. Och eftersom tyngdkraften alltid verkar vinkelrätt mot banan förändrar det inte satellitens hastighet.

I detta fall fungerar tyngdkraften som en centripetalkraft, att det inte är en speciell klass eller bortsett från kraft, utan en som i fallet med satelliten är radiellt riktad mot jordens centrum.

I andra typer av cirkulär rörelse, till exempel en bil som tar en kurva, tolkas rollen som centripetalkraft av statisk gnuggkraft som tvingar mobilen att vända.

Formler för centripetalacceleration

Centripetal -accelerationen beräknas av uttrycket:

AC = v²/r

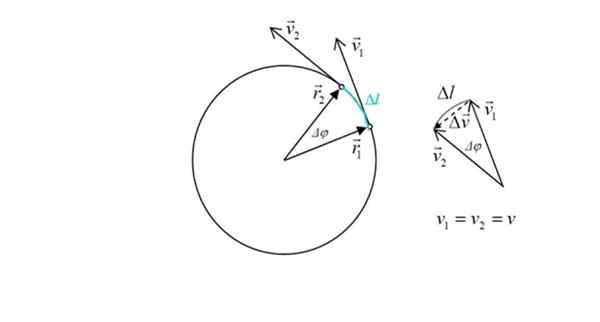Diagram för beräkning av centripetalacceleration i en mobil med MCU. Källa: Källa: Ilevanat [CC BY-SA 3.0 (https: // CreativeCommons.Org/licenser/BY-SA/3.0)]

Detta uttryck kommer att härledas nedan. Per definition är accelerationen variationen i hastighet i tid:

Det kan tjäna dig: Ljuskällor: Typer och enheter som avger ljus

Toppdiagrammet visar i den vänstra figuren, två punkter genom vilka en mobil passerar som rör sig på en radiocirkel r i antihorarium. Observera att hastighetens storlek är densamma i båda fallen, men inte riktningen eller betydelsen.

Mobilen använder tid Δt På turnén, som är liten, eftersom punkterna är mycket nära.

Figuren visar också två positionsvektorer r₁ och r₂, vars modul är densamma: radion r av omkretsen. Vinkeln mellan båda punkterna är Δφ. I grönt rosett Tour of the Mobile, betecknad som Δl.

I figuren till höger ser man att storleken på Δv, Förändringen i hastighet är ungefär proportionell mot ΔL, eftersom vinkeln Δφ är liten. Men förändringen i hastighet är relaterad exakt till acceleration. Triangeln varnas av summan av vektorer som:

v₁ + Δv = v₂ → 5v = v₂ - v₁

Δv Det är intressant, eftersom det är proportionellt mot centripetalacceleration. Från figuren varnas det för att vara liten vinkel Δφ, vektor Δv Det är i vinkelrätt essens båda v₁ tycka om v₂ och pekar på centrum av omkretsen.

Även om vektorerna sticker ut med fetstil, för effekterna av geometrisk natur som följer, arbetar vi med modulerna eller storleken på dessa vektorer, oavsett vektorotation.

Något annat: Du måste använda definitionen av central vinkel, vilket är:

Δφ= 5l/r

Nu jämförs båda siffrorna, som är proportionella eftersom vinkeln 5φ det är vanligt:

Kan tjäna dig: vad är polariserat ljus?

 

Dividering mellan ΔT:

 Eftersom definitionen av hastighet är V = ΔL/ ΔT. Men ΔV/ Δt Det är just storleken på centripetalacceleration, vilket är vad som söks. På detta sätt nås uttrycket i början:

till_c= v²/r

Träning löst

En partikel rör sig i en cirkel av 2.70 m radio. Vid en viss tid är accelerationen 1.05 m/s² I en riktning som gör en vinkel på 32.0º med rörelsedirektoratet. Beräkna din hastighet:

a) Vid den tiden

b) 2.00 sekunder senare, förutsatt konstant tangentiell acceleration.

Svar

Det är en varierad cirkulär rörelse, eftersom uttalandet indikerar att accelerationen har en given vinkel med rörelsens riktning som inte är eller 0º (det kan inte vara en cirkulär rörelse) eller 90º (det skulle vara en enhetlig cirkulär rörelse).

Därför samexisterar de två komponenterna - radiella och tangentiella - samexisterar. Kommer att betecknas som_c redan_t och visas ritad i följande figur. Den gröna vektorn är nettoaccelerationsvektorn eller helt enkelt acceleration till.

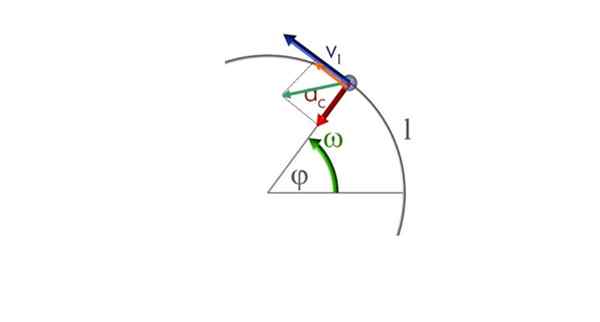En partikel rör sig i en cirkulär bana i en antihorary mening och varierad cirkulär rörelse. Källa: Commons.Wikimedia.org

a) Beräkning av accelerationskomponenter

till_c = a.cos θ = 1.05 m/s² . cos 32.0º = 0.89 m/s² (i rött)

till_t = a.synd θ = 1.05 m/s² . Sen 32.0º = 0.57 m/s² (i orange)

Beräkning av mobilhastighet

Sedan a_c = v²/r, så:
b) 2 sekunder senare hastigheten v kommer att ökas tack vare den tangentiella komponenten i accelerationen

v = v_antingen +till_t. T = 1.6 m/s + (0.57 x 2) m/s = 2.74 m/s

Referenser

1. Giancoli, D. Fysik. 2006. Principer med applikationer. Sjätte upplagan. Prentice hall. 107-108.
2. Hewitt, Paul. 2012. Konceptuell fysisk vetenskap. Femte upplagan.Pearson.106 - 108.