Antiderivativa formler och ekvationer, exempel, övningar

En antiderivativ F (x) av en funktion F(x) kallas också primitiv eller helt enkelt den obestämda integralen av nämnda funktion, om det är i ett givet intervall Yo, Är det sant att F '(x) = f (x)

Låt oss till exempel ta följande funktion:

f (x) = 4x³

Ett antiderivativ av denna funktion är f (x) = x⁴, Eftersom genom att härleda f (x) genom härledningsregeln för befogenheterna:

Det erhålls exakt f (x) = 4x³.

Detta är emellertid bara ett av de många antiderivativen för f (x), eftersom denna andra funktion: g (x) = x⁴ + 2 Det är också, för genom att härleda g (x) med avseende på x är det detsamma erhålls tillbaka f (x).

Låt oss kontrollera det:

Kom ihåg att den som härrör från en konstant är 0. Därför till termen x⁴ Du kan lägga till valfri konstant och dess derivat fortsätter att vara 4x³.

Det dras slutsatsen att alla funktioner i den allmänna formen f (x) = x⁴ + C, där c är en verklig konstant, fungerar som antiderivativ för f (x).

Det tidigare illustrativa exemplet kan uttryckas enligt följande:

df (x) = 4x³ Dx

Det odefinierade antiderivatet eller integralen uttrycks med symbolen ∫ därför:

F (x) = ∫4x³ dx = x⁴ + C

Där funktionen f (x) = 4x³  Det kallas integrerande, och C är Integrationskonstant.

[TOC]

Exempel på antiderivativ

Figur 1. Anti -Hotley är inget annat än en obestämd integral. Källa: Pixabay.

Att hitta ett antiderivativ av en funktion är i vissa fall enkelt där derivaten är välkända. Till exempel, vara funktionen f (x) = sen x, en oteriverad för det är en annan funktion f (x), så att vid härledd den erhålls f (x).

Den funktionen kan vara:

F (x) = - cos x

Låt oss kontrollera att det är sant:

F '(x) = (- cos x)' =- (-sen x) = sin x

Därför kan vi skriva:

∫sen x dx = -cos x + c

Förutom att känna till derivaten finns det grundläggande och enkla integrationsregler för att hitta obestämd antiderivativ eller integrerad.

Kan tjäna dig: successiva derivat

Var en riktig konstant, då:

1.- ∫kdx = k ∫dx = kx + c

2.- ∫kf (x) dx = k ∫f (x) dx

Om en H (x) -funktion kan uttryckas som summan eller subtraktionen av två funktioner, är dess obestämda integral:

3.- ∫h (x) dx = ∫ [f (x) ± g (x)] dx = ∫f (x) dx ± ∫g (x) dx

Detta är egenskapen till linearitet.

De Maktregel För integraler kan det upprättas på detta sätt:

Denna regel har en uppenbar begränsning: sedan nämnaren N +1 Det kan inte göras 0, därför n ≠ -1.

När det gäller n = -1 används följande regel:

5.- ∫x ^-1 Dx = ln x +c

Det är lätt att visa att derivatet av ln x det är just x ^-1.

Differentiella ekvationer

En differentiell ekvation är en där det okända är som ett derivat.

Nu, från den tidigare analysen, är det lätt att inse att den omvända operationen till derivatet är det odefinierade antiderivatet eller integrerat.

Låt f (x) = y '(x), det vill säga härrörande från en viss funktion. Vi kan använda följande notation för att indikera detta derivat:

Det följer omedelbart det:

dy = f (x) dx

Det okända av differentiell ekvation är funktionen y (x), den vars derivat är f (x). För att rensa det är det föregående uttrycket integrerat på båda sidor, vilket motsvarar tillämpningen av antiderivatet:

∫dy = ∫f (x) dx

Den vänstra integralen löses genom integrationsregel 1, med k = 1 och därmed rensas den eftertraktade -Aite:

och (x) = ∫f (x) dx = f (x) + c

Och eftersom C är en verklig konstant, för att veta vilken som är lämplig i båda fallen, måste uttalandet innehålla tillräcklig ytterligare information för att beräkna värdet på C. Det här kallas Initialtillstånd.

Vi kommer att se exempel på tillämpning av allt detta i nästa avsnitt.

Kan tjäna dig: punktlig uppskattning

Antideriverade övningar

- Övning 1

Tillämpa integrationsreglerna för att få följande odefinierade antiderivativ eller integraler i de angivna funktioner, vilket förenklar resultaten så mycket som möjligt. Det är bekvämt att verifiera resultatet genom härledningen.

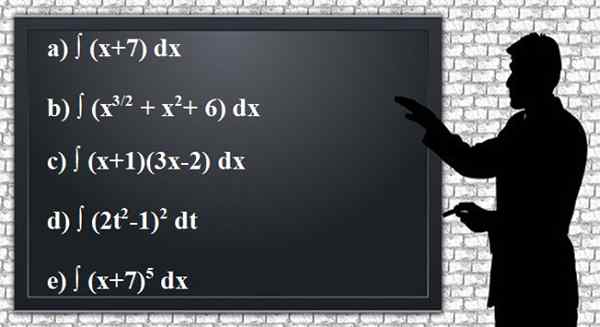figur 2. Definierade anteriverade eller integrerade övningar. Källa: Pixabay.

Lösning till

Vi tillämpar först regel 3, eftersom integrationen är summan av två termer:

∫ (x +7) dx = ∫ xdx +∫7dx

För den första integralen tillämpas makternas regel:

∫ xdx = (x² /2)+c₁

I den andra integrerade regel 1 gäller att vara k = 7:

∫7dx = 7∫dx = 7x + c₂

Och nu läggs resultaten till. De två konstanterna grupperas i en, generellt kallad C:

∫ (x+7) dx = (x² /2) + 7x + c

Lösning B

Genom linearitet sönderdelas denna integrerade i tre enklare integraler, till vilka makternas regel kommer att tillämpas:

∫ (x^3/2 + x² + 6) dx = ∫x^3/2 Dx + ∫x² dx +∫6 dx =

= (2/5) x^5/2 + (1/3) x³ + 6x + c

Observera att en integrationskonstant för varje integrering visas, men de möts i ett enda samtal C.

Lösning C

I det här fallet är det bekvämt att tillämpa multiplikationens distributiva egenskap för att utveckla integrationen. Sedan använder du makternas regel för att hitta varje integral separat, som föregående år.

∫ (x+1) (3x-2) dx = ∫ (3x²-2x+3x-2) dx = ∫ (3x² + X - 2) dx

Den uppmärksamma läsaren kommer att observera att de två centrala termerna är liknande, därför reduceras de innan de integreras:

∫ (x+1) (3x-2) dx = ∫3x² dx + ∫ x dx + ∫- 2 dx = x³ + (1/2) x² - 2x + c

Lösning E

Ett sätt att lösa integralen skulle vara att utveckla kraft, som gjordes i exempel D. Men eftersom exponenten är högre, skulle det vara nödvändigt att göra en variabel förändring, för att inte behöva göra en så lång utveckling.

Kan tjäna dig: kontinuerlig slumpmässig variabel

Den variabla förändringen är som följer:

U = x + 7

Härleda på båda sidor detta uttryck:

du = dx

Integrationen förvandlas till en enklare med den nya variabeln, som löses med styrregeln:

∫ (x+7)⁵ Dx = ∫ u⁵ du = (1/6) u⁶ + C

Slutligen återförs förändringen för att återgå till den ursprungliga variabeln:

∫ (x+7)⁵ Dx = (1/6) (x+7)⁶ + C

- Övning 2

En partikel är initialt i vila och rör sig längs X -axeln. Dess acceleration för t> 0 ges av funktion a (t) = cos t. Det är känt att vid t = 0 är positionen x = 3, alla i enheter i det internationella systemet. Det uppmanas att hitta hastighet V (t) och position x (t) för partikeln.

Lösning

Eftersom acceleration är den första härledda från hastighet med avseende på tid har du följande differentiella ekvation:

a (t) = v '(t) = cos t

Det följer att:

v (t) = ∫ cos t dt = sin t + c₁

Å andra sidan vet vi att hastigheten i sin tur är derivatet av positionen, därför integrerar vi igen:

x (t) = ∫ V (t) dt = ∫ (sin t + c₁) dt = ∫sen t dt + ∫c₁ dt = - cos t + c₁ t + c₂

Integrationskonstanter bestäms utifrån informationen i uttalandet. Först säger han att partikeln ursprungligen var i vila, därför v (0) = 0:

V (0) = sin 0 + c₁ = 0

C₁ = 0

Då måste du x (0) = 3:

x (0) = - cos 0 + c₁ 0 + c₂ = - 1 + c₂ = 3 → C₂ = 3+1 = 4

Hastighets- och positionsfunktioner är definitivt så här:

v (t) = sen t

x (t) = - cos t + 4

Referenser

1. Engler, a. 2019. Integrerad kalkyl. National University of the Coast.
2. Larson, r. 2010. Beräkning av en variabel. 9na. Utgåva. McGraw Hill.
3. Gratis matematiktexter. Antiderivat. Återhämtat sig från: matematik.Liibretexts.org.
4. Wikipedia. Antiderivativ. Hämtad från: i.Wikipedia.org.
5. Wikipedia. Obestämd integration. Återhämtad från: är.Wikipedia.org.