Elektrisk potential formel och ekvationer, beräkning, exempel, övningar

han elektrisk potential Det definieras när som helst där det finns ett elektriskt fält, till exempel den potentiella energin för nämnda fält per lastenhet. Specifika belastningar och fördelningar av specifika eller kontinuerliga belastningar producerar elektriskt fält och har därför en potential associerad.

I det internationella enhetssystemet (SI) mäts den elektriska potentialen i volt (V) och betecknas som V. Matematiskt uttrycker som:

V = u/q_antingen

Figur 1. Hjälpskablar anslutna till ett batteri. Källa: Pixabay.

Där du är den potentiella energin förknippad med belastning eller distribution och q_antingen Det är en positiv provbelastning. Eftersom du är en skalar är potentialen också.

Från definitionen är 1 volt helt enkelt 1 Joule /Coulomb.

Anta en punktlig börda som. Vi kan verifiera arten av fältet som denna belastning producerar genom en positiv och liten provbelastning, kallad Q_antingen, Används som en sond.

Det arbete som krävs för att flytta denna lilla belastning från punkten till Fram till punkten b, är det negativa av skillnaden i potentiell energi ΔU mellan dessa punkter:

W_{A → B} = -Δu = - (u_b - ELLER_till)      

Dela allt mellan Q_antingen:

W_{A → B} /Q_antingen= - Δu / q_antingen = - (u_b - ELLER_till) /Q_antingen = - (v_b - V_till) = -ΔV

Här v_b Det är potentialen vid punkt B och V_till är poängen a. Potentialskillnaden v_till - V_b  är potentialen för När det gäller B och kallas V_Ab. Ordern på abonnemanget är viktigt, om det ändrades, då potentialen för B.

[TOC]

Elektrisk potentialskillnad

Från ovannämnda följer det:

-ΔV = W_{A → B} /Q_antingen

Därför:

ΔV = -w_{A → B} /Q_antingen

Nu beräknas arbetet som integralen i skalprodukten mellan den elektriska kraften F mellan Q och Q_antingen och förskjutningsvektorn Dℓ Mellan punkterna A och B. Eftersom det elektriska fältet är kraft per lastenhet:

OCH = F/Q_antingen

Arbetet för att bära testbelastningen från A till B är:

Denna ekvation erbjuder sättet att direkt beräkna potentialskillnaden om elektricitet eller distribution av elektriska fält som producerar det tidigare är känt.

Och det varnas också för att potentialskillnaden är en skalarkvantitet, till skillnad från det elektriska fältet, som är en vektor.

Kan tjäna dig: Magnetism: Magnetiska egenskaper hos material, användning

Tecken och värden för potentiell skillnad

Från föregående definition observerar vi att om OCH och Dℓ De är vinkelräta, potentialskillnaden ΔV är noll. Detta betyder inte att potentialen vid sådana punkter är noll, utan helt enkelt v_till = V_b, det vill säga, potentialen är konstant.

Linjerna och ytorna där detta händer kallas Lag. Till exempel är utrustningslinjerna i fältet för en punktlig belastning koncentriska omkretsar till lasten. Och teamCotential Surfaces är koncentriska sfärer.

Om potentialen produceras av en positiv belastning, vars elektriska fält består av utgående radiolinje. Som testbelastningen q_antingen Det är positivt, det känns mindre elektrostatisk avstötning ju längre det är från Q.

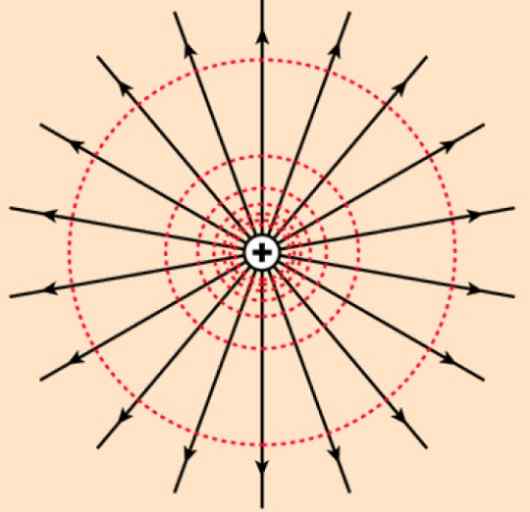figur 2. Elektriskt fält producerat av en positiv punktlig belastning och dess utrustning (röd) linjer: Källa: Wikimedia Commons. Hyperphysics/CC BY-SA (https: // Creativecommons.Org/licenser/BY-SA/4.0).

Tvärtom, om lasten q Det är negativt, försöksbelastningen q_antingen (positivt) kommer att vara mindre potential när det närmar sig q.

Hur man beräknar den elektriska potentialen?

Integrationen som ges ovan tjänar till att hitta potentialskillnaden, och därför potentialen vid en given punkt b, Om referenspotentialen är känd vid en annan punkt till.

Till exempel är det fallet med en punktlig belastning q, vars elektriska fältvektor vid en punkt belägen på avstånd r av lasten är:

OCH = kq/r² r

Där k är den elektrostatiska konstanten vars värde i enheter i det internationella systemet är:

K = 9 x 10 ⁹ Nm² /C².

Och vektorn r Det är enhetsvektorn längs linjen som förenar q med punkt P.

Det ersätts i definitionen av ΔV:

Väljer att poängen b vara på avstånd r av lasten och att när du ska → ∞ den potential värda 0, då v_till = 0 och föregående ekvation är som:

V = kq/r

Välj v_till = 0 När → ∞ Det är meningsfullt, för vid en punkt långt ifrån lasten är det svårt att uppfatta att den finns.

Elektrisk potential för diskreta belastningsfördelningar

När det finns många specifika belastningar som fördelas i en region beräknas den elektriska potentialen som de producerar när som helst P i utrymmet, vilket lägger till de individuella potentialerna som produceras av var och en. Så:

Kan tjäna dig: elliptisk rörelse

V = v₁ + V₂ + V₃ +... vn = ∑ V_Yo

Summan utvidgas från i = till n och potentialen för varje belastning beräknas av ekvationen som anges i föregående avsnitt.

Elektrisk potential i kontinuerliga belastningsfördelningar

Från potentialen för en punktlig last kan du hitta potentialen som producerar ett laddat objekt, med en mätbar storlek, när som helst.

För detta är kroppen uppdelad i många små oändliga laster DQ. Var och en bidrar till den totala potentialen med en Dv oändligt liten.

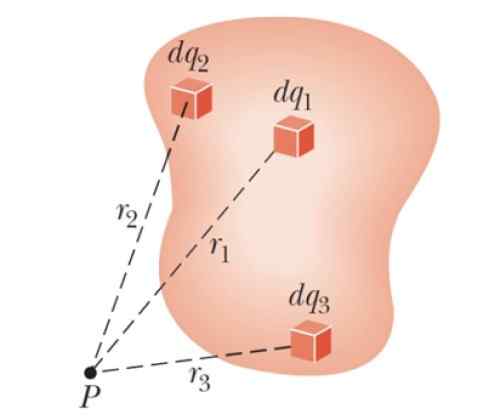Figur 3. Schema för att hitta den elektriska potentialen för en kontinuerlig distribution vid punkt P. Källa: Serway, R. Fysik för vetenskap och teknik.

Sedan läggs alla dessa bidrag till genom en integral och den totala potentialen erhålls således:

Denna metod gör det möjligt att beräkna potentialskillnaden utan att tidigare veta det elektriska fältet, men den tillämpas endast på ändliga lastfördelningar, till exempel mycket tunna staplar laddade och ändliga längd, ringar, skivor och cylindrar med ändlig längd, till exempel.

Exempel på elektrisk potential

Det finns elektrisk potential på olika enheter tack vare vilka det är möjligt. Elektriska potentialer är också etablerade i naturen när det finns åskväder.

Batterier och batterier

I batterierna och batterierna lagras el genom de kemiska reaktionerna inuti. Dessa inträffar när kretsen stängs, vilket gör att den kontinuerliga strömmen kan flyta och en glödlampa slås på, eller bilstartmotorn fungerar.

Det finns olika spänningar: 1.5 V, 3 V, 9 V och 12 V är de vanligaste.

Utlopp

Till ett inbyggt skott på väggen är artefakter och apparater som arbetar med den kommersiella elen för växelström ansluten. Beroende på plats kan spänningen vara 120 V eller 240 V.

Figur 4. När man tar väggen finns det en potentiell skillnad. Källa: Pixabay.

Spänning mellan laddade moln och marken

Det är den som inträffar under stormarna på grund av den elektriska laddningsrörelsen genom atmosfären. Det kan vara i storleksordningen 10⁸ V.

Figur 5. Elektrisk storm. Källa: Wikimedia Commons. Sebastien d'Ec Arc, Animation av Koba-chan/CC BY-SA (https: // Creativecommons.Org/licenser/BY-SA/2.5)

Van der graffgenerator

Tack vare ett transportgummitejp produceras en gnidning genom att gnugga, som ackumuleras på en ledande sfär på en isolerande cylinder. Detta genererar en potentiell skillnad som kan vara flera miljoner volt.

Kan tjäna dig: konvektion Figur 6. Van der Graff Generator på elteatern i Boston Sciences Museum. Källa: Wikimedia. Boston Museum of Science/CC BY-S (https: // Creativecommons.Org/licenser/BY-SA/3.0) Commons.

Elektrokardiogram och elektroencefalogram

I hjärtat finns specialiserade celler som polariserar och depolariserar ursprungliga skillnader. Dessa kan mätas beroende på tid med ett elektrokardiogram.

Denna enkla tentamen utförs genom att placera elektroder på personens bröst, kan mäta små signaler.

Eftersom de är mycket låga spänningar måste du förstärka dem bekvämt och sedan spela in dem på ett pappersband eller se dem genom datorn. Läkaren analyserar pulserna på jakt efter avvikelser och upptäcker därmed hjärtproblem.

Figur 7. Tryckt elektrokardiogram. Källa: PXFuel.

Hjärnans elektriska aktivitet kan också registreras med en liknande procedur, kallad elektroencefalogram.

Träning löst

En last Q = - 50.0 NC ligger vid 0.30 m av punkten TILL och 0.50 m punkt B, som visas i följande figur. Svara på följande frågor:

a) Vad är potentialen i en producerad av denna last?

b) och vad är potentialen i B?

c) Om en last som rör sig från A till B, vad är den potentiella skillnaden genom vilken den gör?

d) Enligt det tidigare svaret ökar eller minskar dess potentiella ökning eller minskar?

e) Ja Q = - 1.0 NC, vad är förändringen i din elektrostatiska potentiella energi när du flyttar från A till B?

f) Hur mycket arbete producerar det elektriska fältet av Q medan testbelastningen rör sig från A till B?

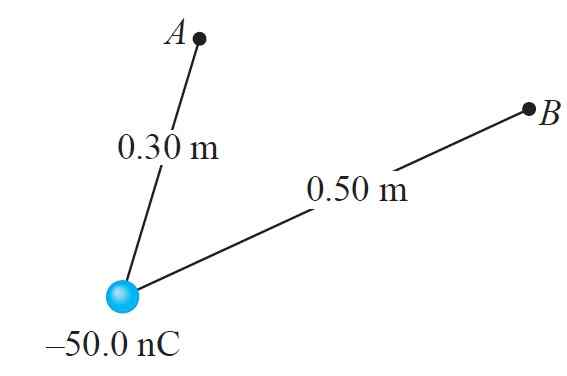Figur 8. Schema för övningen löst. Källa: Giambattista, a. Fysik.

Lösning till

Q är en punktlig belastning, därför beräknas dess elektriska potential i A av:

V_TILL = kq/r_TILL = 9 x 10⁹ X (-50 x 10^-9) / 0.3 V = -1500 V

Lösning B

Liknande

V_B = kq/r_B = 9 x 10⁹ X (-50 x 10^-9) / 0.5 V = -900 V

Lösning C

ΔV = v_b - V_till = -900 -( -1500) V = + 600 V

Lösning D

Om belastningen som är positiv ökar, ökar, men om den är negativ minskar dess potential.

Lösning E

ΔV = Δu/q_antingen → ΔU = q_antingen ΔV = -1.0 x 10^-9 x 600 j = -6.0 x 10^-7 J.

Det negativa inloggningen Δu indikerar att den potentiella energin i B är mindre än för a.

Lösning f

Eftersom w = -Δu fältet presterar +6.0 x 10^-7 J av arbete.

Referenser

1. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volym 5. Elektrostatik. Redigerad av Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fysik. 2: a. Ed. McGraw Hill.
3. Resnick, r. (1999). Fysisk. Vul. 2. 3: e upplagan. på spanska. Kontinentala redaktionella företag s.TILL. av C.V.
4. Tipler, s. (2006) Fysik för vetenskap och teknik. 5: e upplagan. Volym 2. Redaktör.
5. Serway, R. Fysik för vetenskap och teknik. Volym 2. 7th. Ed. Cengage Learning.