Konjugerad binomial hur det löses, exempel, övningar

En Konjugerad binomial Från en annan binomial är en där de bara skiljer sig åt med ett tecken på operationen. Binomialen, som namnet antyder, är en algebraisk struktur som består av två termer.

Några exempel på binomials är: (A + B), (3M - N) och (5x - y). Och deras respektive konjugerade binomialer är: (a - b), (-3 m - n) och (5x + y). Som kan ses omedelbart är skillnaden i skylten.

Figur 1. En binomial och dess konjugerade binomial. De har samma termer, men skiljer sig åt i skylten. Källa: f. Zapata.

En binomial multiplicerad med dess konjugat resulterar i en anmärkningsvärd produkt som används mycket i algebra och vetenskap. Resultatet av multiplikation är subtraktionen av rutorna i termerna för den ursprungliga binomialen.

Till exempel, (X - y) Det är en binomial och dess konjugat är (x + y). Sedan är produkten från de två binomialerna skillnaden mellan torgen i termerna:

(X - y).(x + y) = x² - och²

[TOC]

Hur löses en konjugerad binomial?

Regeln som anges med de konjugerade binomialerna är som följer: 

Produkten av två konjugat binomials är lika med kvadratet för den första termen minus kvadratet för den andra terminen. Detta resultat kallas fyrkantig skillnad.

Som ett exempel på applikationen börjar vi med att demonstrera det tidigare resultatet, vilket kan göras med hjälp av produktens distributiva egenskap med avseende på den algebraiska summan.

(x - y) (x + y) = x.x + x.och och.X - y.och

Den föregående multiplikationen erhölls efter dessa steg:

- Den första terminen i den första binomialen multipliceras med den första terminen i den andra

- Sedan den första av den första, för den andra av den andra

- Sedan den andra av den första för den första av den andra 

- Slutligen den andra av den första för den andra av den andra.

Kan tjäna dig: vektoralgebra

Låt oss nu göra en liten förändring med kommutativ egendom: och.x = x.och. Det återstår så här:

(x - y) (x + y) = x.x + x.y - x.och och.och

Eftersom det finns två lika villkor men annars (markeras i färg och understrukna), avbryts de och förenklas:

(x - y) (x + y) = x.X - y.och

Slutligen tillämpas det att multiplicera ett nummer av sig själv motsvarar att lyfta den kvadrat, så x.x = x² och även och.y = y².

På detta sätt, vad som hade påpekats i föregående avsnitt, att produkten av en summa för sin skillnad är skillnaden mellan rutorna:

(X - y).(x + y) = x² - och²

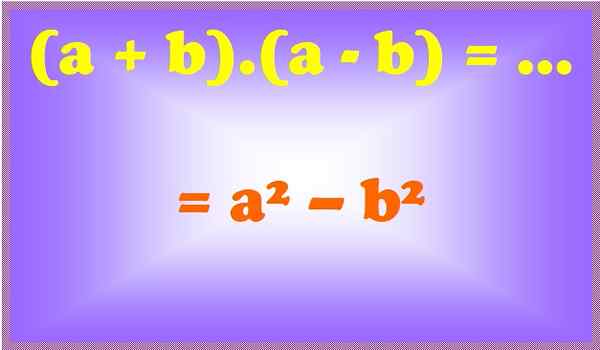figur 2. En summa för sin skillnad är en skillnad i rutor. Källa: f. Zapata.

Exempel

- Konjugerade binomials av olika uttryck

Exempel 1

Hitta konjugatet av (och² - 3y).

Svar: (och² + 3y)

Exempel 2

Få produkten av (och² - 3y) för sitt konjugat.

Svar: (och² - 3y) (och² + 3y) = (och²)² - (3y)² = y⁴ - 3² och² = y⁴ - 9y²

Exempel 3

Utveckla produkten (1 + 2a).(2a -1).

Svar: Det föregående uttrycket motsvarar (2a + 1).(2a -1), det vill säga det motsvarar produkten av en binomial för dess konjugat.

Det är känt att produkten av en binomial för dess konjugerade binomial är lika med skillnaden mellan kvadrarna i binomialtermerna:

(2a + 1) (2a -1) = (2a)² - 1² = 4 a² - 1

Exempel 4

Skriv produkten (x + y + z) (x - y - z) som en skillnad i rutor.

Svar: Vi kan assimilera trinomialerna före formen av konjugerade binomialer, vilket använder noggrant parentes och fyrkantiga parenteser:

(x + y + z) (x - y - z) = [x + (y + z)] [x - (y + z)]

På detta sätt kan skillnaden mellan rutor tillämpas:

(x + y + z) (x - y - z) = [x + (y + z)].[x - (y+z)] = x² - (Y+z)²

Exempel 5

Uttrycka produkten (m² - m -1).(m² + m -1) som en skillnad i rutor.

Kan tjäna dig: 120 delare

Svar: Det föregående uttrycket är produkten från två trinomialer. Först måste det skrivas om som produkten av två konjugerade binomialer:

(m² - m -1) (m² + m -1) = (m² - 1 - m) (m² -1 + m) = [(m² -1) - m].[(m² -1) +m)]

Vi tillämpar det faktum att produkten från en binomial genom dess konjugat är den kvadratiska skillnaden i dess termer, som förklarats:

[(m² -1) - m].[(m² -1) +m)] = (m² -1)² - m²

Övningar

Som alltid börjar det med de enklaste övningarna och då höjer komplexiteten.

- Övning 1

Escriba (9 - a²) som en produkt.

Lösning

Först skriver vi om uttrycket som en skillnad i rutor för att tillämpa det som förklarats tidigare. Därför:

(9 - A²) = (3² - till²)

Vi faktor omedelbart, vilket motsvarar att skriva denna skillnad i rutor som en produkt, som begärs i uttalandet:

(9 - A²) = (3² - till²) = (3 + a) (3 -a)

- Övning 2

Faktorisera 16x² - 9y⁴.

Lösning

Faktor ett uttryck betyder att skriva det som en produkt. I det här fallet är det nödvändigt att tidigare skriva om uttrycket, att få en skillnad i rutor.

Det är inte svårt att göra det, eftersom alla faktorer noggrant observerar är perfekta rutor. Till exempel 16 är kvadratet av 4, 9 är kvadratet av 3, och⁴ är kvadratet av och² och x² är kvadratet av X:

16x² - 9y⁴  = 4²x² - 3²och⁴ = 4²x²  - 3²(och²)²

Sedan tillämpas det vi redan: att en skillnad i rutor är produkten av konjugerade binomials:

(4x)² - (3 och²)² = (4x - 3 och²) . (4x + 3 och²)

- Övning 3

Skriv (a - b) som en binomial produkt

Lösning

Den tidigare skillnaden bör skrivas som fyrkantiga skillnader

(√a)² -(√b)²

Sedan tillämpas det att skillnaden i rutor är produkten från de konjugerade binomialerna

Kan tjäna dig: Minskning av liknande termer

(√a - √b) (√a + √b)

- Övning 4

En av användningarna av det konjugerade binomialet är rationaliseringen av algebraiska uttryck. Denna procedur består i att eliminera rötterna till nämnaren för ett fraktionellt uttryck, som vid flera tillfällen underlättar operationer. Det uppmanas att använda det konjugerade binomialet för att rationalisera följande uttryck:

√ (2 -x) / [√3 - √ (2+x)]]]

Lösning

Den första är att identifiera nämnarens konjugerade binomial: [√3 + √ (2 + x)]].

Nu multiplicerar vi teller och nämnaren av det ursprungliga uttrycket med det konjugerade binomialet:

√ (2 -x) [√3+√ (2+x)] /[√3 - √ (2+x)].[√3 + √ (2 + x)]

I nämnaren för det tidigare uttrycket känner vi igen produkten av en skillnad med en summa, som vi redan vet som motsvarar skillnaden mellan binomialernas rutor:

√ (2-x) .[√3 + √ (2 + x)] /(√3)² - [√ (2+x)]² 

Förenkla nämnaren är:

√ (2-x).[√3+√ (2+x)] / [3 - (2+x)] = √ (2 -x). [√3 + √ (2 + x)] / (1 - x)

Nu tar vi hand om telleren, för vilken vi kommer att tillämpa produktens distributiva egendom med avseende på summan:

√ (2-x) .[√3 + √ (2 + x)] / (1 - x) = √ (6-3x) + √ [(2 -x) (2 + x)] / (1 - x)

I det tidigare uttrycket känner vi igen produkten från binomialen (2-x) för dess konjugat, som är den anmärkningsvärda produkten som är lika med skillnaden i rutor. På detta sätt erhålls slutligen ett rationaliserat och förenklat uttryck:

[√ (6-3x) + √ (4-x²)] / (1 - x)

- Övning 5

Utveckla följande produkt med hjälp av egenskaperna hos den konjugerade binomialen:

[2: a^{(x + 3y)} - 3: e^{(x - 3y)}].[2: a^{(x + 3y)} + 3: e^{(x - 3y)}]

Lösning

4th^{(2x + 6y)} - 9th^{(2x - 6y)} = 4A^(2x) .till^(6y) - 9th^(2x) .till^(-6y)= [4A^(6y) - 9th^(-6y)] .till^(2x)

Den uppmärksamma läsaren kommer att ha märkt den gemensamma faktorn som har markerats i färg.

Referenser

1. Baldor, a. 1991. Algebra. Venezuelan kulturell redaktion.TILL.
2. González J. Konjugerade binomiala övningar. Återhämtat sig från: akademin.Edu.
3. Matematik Alex. Anmärkningsvärda produkter. Återhämtat sig från YouTube.com.
4. Matematik. Konjugerade binomials/ anmärkningsvärda produkter. Återhämtat sig från YouTube.com.
5. Konjugerade binomialprodukter. Återhämtat sig från: lms.Colbachenlinea.mx.
6. Vital. Konjugerade binomialer. Återhämtat sig från: YouTube.com.