Vågegenskaper

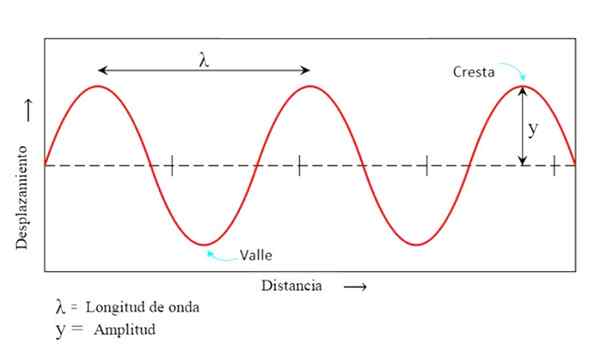
Figur 1. Representativa parametrar för en sinusformad våg. Källa: f. Zapata.

De Vågegenskaper De är det utmärkande med det böljande fenomenet: våglängden, frekvensen, dalarna, åsarna, hastigheten, energin och andra som vi kommer att förklara i den här artikeln.

I vågor är det inte partiklar som reser med störningar, utan energi. När en våg sprider sig i ett materiellt medium, som kan vara vatten, luft eller ett rep, bland andra, rör sig partiklarna bara från jämviktspositionen, för att återgå till det efter en kort tid.

Rörelsen överförs emellertid från en partikel till en annan, vilket gör att var och en av dem vibrerar. På detta sätt sprider störningen i mitten viva, Som fansvågen gör på stadionerna, när fotbollsmatcher spelas.

Studien av vågor är mycket intressant, eftersom vi lever i en värld full av dem: ljus, havsvågor, ljudet av musik och röst är alla böljande fenomen, även om av olika natur. Både ljus och ljud är särskilt viktiga, eftersom vi ständigt behöver dem för att kommunicera med omvärlden.

Vilka är egenskaperna hos vågorna?

Vibration

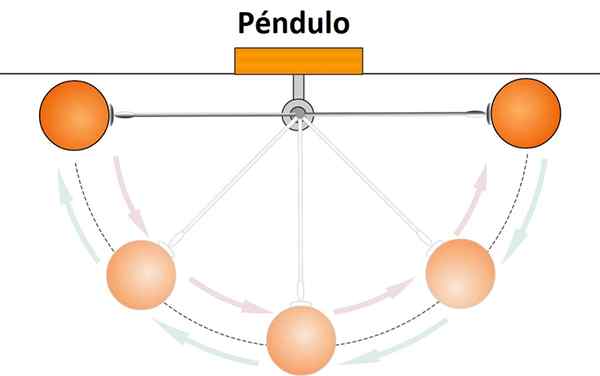
Det är den kompletta turnén som gör en partikel i sin svängande rörelse. Till exempel har en pendel en rörelse av svängning, eftersom den från en viss punkt beskriver en båge, stannar när den når en viss höjd och återgår till sin ursprungliga position.

Om det inte var för friktion skulle denna rörelse följa på obestämd tid. Men på grund av friktion blir rörelsen långsammare och långsammare och den minst breda svängningen, tills pendeln stannar.

Det kan tjäna dig: andra lagen om termodynamik: formler, ekvationer, exempel

När ett horisontellt spetsrep störs, vibrerar partiklarna i repet i vertikal riktning, det vill säga från topp till botten, medan störningen reser horisontellt längs repet.

Svängningscenter

När en partikel gör sin svängande rörelse gör den att den rör sig med avseende på en viss punkt, kallad ursprung eller oscillationscenter.

I exemplet med pendeln är det i jämvikt vid den lägsta punkten och svänger runt detta om vi skiljer det lite från denna position. Därför kan denna punkt betraktas som centrum för svängningen.

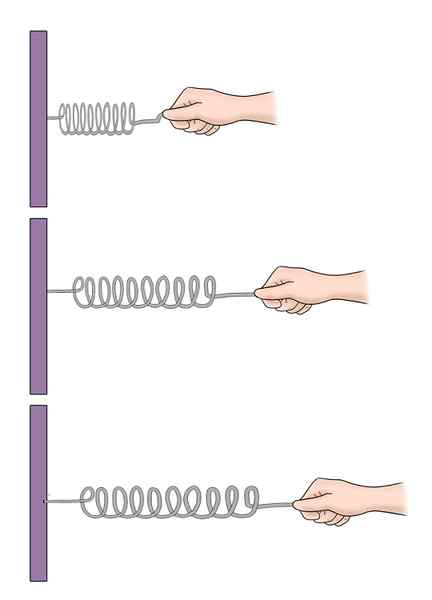
Vi kan också föreställa oss en fjäder eller fjäder på ett horisontellt bord, föremål i ena änden till en vägg, och med ett block i den andra änden. Om fjäderbrush-systemet är ostörande är blocket i en viss jämviktsposition.

Men när du komprimerar eller sträcker våren lite börjar systemet svänga runt den jämviktspositionen.

Förlängning

Det är avståndet som partikeln flyttar bort från svängningscentret efter ett tag. Det mäts i meter när det internationella systemet används om.

Om en fjäder är komprimerad eller sträckt med ett block i ena änden, sägs det att det har upplevt en förlängning av "x" antal meter, centimeter eller enheten som används för att mäta avstånd.

Åsar och dalar

De är respektive de högsta och lägsta punkter som partikeln når med avseende på jämviktspositionen y = 0 (se figur 1).

Amplitud

Havets vågor, när de har mycket amplitud som denna, bär mycket energi

Det är det maximala avståndet som partikeln skiljer sig från oscillationscentret och också ges i meter. Det betecknas som TILL eller som och. Där sammanfaller jämviktspositionen med y = 0 och motsvarar åsarna och vågdalarna.

Kan tjäna dig: dynamisk eller kinetisk friktion: koefficient, exempel, övningar

Amplituden är en viktig parameter, eftersom den är relaterad till energin som transporterar vågen. Ju större amplitud, desto större är energi, som med havets vågor, till exempel.

Nod

Noderna är de punkter som partikeln passerar genom oscillationscentret eller jämviktspositionen.

Cykel

Detta kallas en fullständig svängning, när partikeln passerar från en vapen till nästa, eller från en dal till nästa. Då säger vi att han gjorde en cykel.

Pendeln utför en fullständig svängning när en viss höjd av jämviktspositionen flyttas bort, passerar genom den lägsta punkten, stiger till samma höjd på en resa och återgår till den initiala höjden i returresan.

Period

Eftersom vågorna är repetitiva är partikelrörelsen tidningen. Perioden är den tid det tar att göra en fullständig svängning och nekas vanligtvis med bokstaven TuperCase. Periodens enheter i det internationella systemet om de är de andra (erna).

Frekvens

Det är periodens omvända eller ömsesidiga storlek och är relaterad till mängden svängningar eller cykler som görs per tidsenhet. Det betecknas med brevet F.

Eftersom mängden svängningar inte är en enhet, för frekvensen används sekunderna^-1 (s^-1), kallas Hertz eller Hertzios och förkortade HZ.

Eftersom vi är invers av perioden kan vi skriva ett matematiskt förhållande mellan båda storlekarna:

F = 1 /t

Nåväl:

T = 1/f

Om till exempel en pendel kör 30 cykler på 6 sekunder är dess frekvens:

F = (30 cykler)/(6 s) = 5 cykler/s = 5 Hz.

Kan tjäna dig: Relativ densitet: Beräkning, exempel, övningar

Våglängd

Det är avståndet mellan två punkter i en våg som är i samma höjd, förutsatt att en fullständig svängning har utförts. Det kan till exempel mätas från en vapen till en annan på varandra följande, men också från Valle till Valle.

Våglängden betecknas av den grekiska bokstaven λ, som lyder "lambda" och mäts i distansenheter som mätarna i det internationella systemet, även om det finns en så stor variation av våglängder, att multiplarna och submultiplarna är ofta mätare.

Vågnummer

Det är omvänd storlek på våglängden, multiplicerad med nummer 2π. Därför, genom att beteckna vågnumret med bokstav k, har vi:

K = 2π / λ

Utbredningshastighet

Det är den hastighet som störningen reser. Om mediet i vilket vågen förökas är homogent och isotropiskt, det vill säga dess egenskaper är detsamma överallt, är denna hastighet konstant och ges av:

V = λ / t

Enheterna med förökningshastigheten är desamma som de med någon annan hastighet. I det internationella systemet motsvarar M/s.

Eftersom perioden är invers av frekvensen kan det också uttryckas:

v = λ . F

Och eftersom hastigheten är konstant, produkten λ.f också, så att om till exempel våglängden ändras ändras frekvensen så att produkten förblir densamma.

Referenser

1. Giancoli, D.  2006. Fysik: Principer med applikationer. Sjätte. Ed Prentice Hall.
2. Hewitt, Paul. 2012. Konceptuell fysisk vetenskap. Femte. Ed. Pearson.
3. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14th. Ed. Volym 1. Pearson.
4. Serway, R., Jewett, J. (2008). Fysik för vetenskap och teknik. Volym 1. 7th. Ed. Cengage Learning.
5. Tipler, s. (2006) Fysik för vetenskap och teknik. 5: e upplagan. Volym 1. Redaktör.