Elastiska chocker i en dimension, specialfall, övningar

De elastiska chocker o Elastiska kollisioner består av korta men intensiva interaktioner mellan föremål, där både mängden rörelse och kinetisk energi bevaras. Choques är mycket frekventa händelser i naturen: från subatomära partiklar till galaxer, passerar genom biljardbollar och chockbilar i attraktionsparker, alla är föremål som kan kollidera.

Under en kollision eller chock är interaktionskrafterna mellan föremål mycket intensiva, mycket mer än de som kan agera externt. På detta sätt kan det bekräftas att under kollisionen bildar partiklarna ett isolerat system.

Kollisioner mellan biljardbollar kan betraktas som elastiska. Källa: Pixabay.

I det här fallet är det uppfyllt att:

Var P Det är vektormängden rörelse, vars storlek är Mv (Hastighetsmassa). Om derivatet av P är null, det betyder det P det är konstant. Och detta betyder att det inte varierar, att det är bevarat. Därför kan vi bekräfta att:

P_antingen = P_F

Mängden rörelse P_antingen Innan kollision är densamma som efter kollision. Detta uppfylls för alla typer av typen, både elastisk och inelastisk.

Nu måste du överväga följande: Under en kollision upplever objekten en viss deformation. När kollisionen är elastisk återvinner föremål snabbt sin ursprungliga form.

[TOC]

Kinetisk energibesparing

Normalt tillbringas under en chock en del av föremålens energi i värme, deformation, ljud och ibland till och med i att producera ljus. Så systemets kinetiska energi efter kollisionen är mindre än den ursprungliga kinetiska energin.

När kinetisk energi k bevaras den då:

K_antingen = K_F

Vilket innebär att krafterna som agerar under kollisionen är konservativa. Medan kollisionen varar omvandlas den kinetiska energin kort till potentiell energi och sedan är det en kinetisk energi igen. De respektive kinetiska energierna varierar, men summan förblir konstant.

Perfekt elastiska kollisioner är inte ofta, även om biljardbollar är ett ganska bra tillvägagångssätt, liksom kollisioner som äger rum mellan ideala gasmolekyler.

Elastiska chocker i en dimension

Låt oss undersöka en kollision av två partiklar av detta i en enda dimension; Det vill säga de partiklar som interagerar rör sig, säger, längs X -axeln. Anta att de har massor m₁ och m₂. De initiala hastigheterna för var och en är eller₁ och eller₂ respektive. De slutliga hastigheterna är v₁ och v₂.

Vi kan klara oss utan vektorotationen, eftersom rörelsen utförs längs X-axeln, men tecknen (-) och (+) indikerar rörelsen betydelsen. Till vänster är negativ och till den positiva höger, efter konvention.

Kan tjäna dig: Bravais Networks: koncept, egenskaper, exempel, övningar

-Formler för elastiska kollisioner

För mängden rörelse

m₁eller₁ + m₂eller₂ = m₁v₁ + m₂v₂

För kinetisk energi

½ m₁eller²₁ + ½ m₂eller²₂ = ½ m₁v²₁ +  ½ m₂v²₂

När de initiala massorna och hastigheterna är kända är det möjligt att omgruppera ekvationerna för att hitta de slutliga hastigheterna.

Problemet är att det i princip är nödvändigt. Idealet skulle vara att hitta uttryck som inte innehåller dem.

Den första är att göra utan ½ faktor och ordna om båda ekvationerna på ett sådant sätt att ett negativt tecken visas och massorna kan vara faktor:

m₁eller₁ - m₁v₁ = M₂v₂ - m₂eller₂

m₁eller²₁ - m₁v²₁  = +M₂v²₂ - m₂eller²₂

Uttrycks på detta sätt:

m₁(eller₁ - v₁ ) = m₂(v₂ - eller₂)

m₁(eller²₁ - v²₁ ) = m₂ (v²₂ - eller²₂)

Förenkling för att eliminera rutor från hastigheter

Nu måste du använda den anmärkningsvärda produkten, den lägger till dess skillnad i den andra ekvationen, som får ett uttryck som inte innehåller rutorna, som ursprungligen ville:

m₁(eller₁ - v₁ ) = m₂(v₂ - eller₂)

m₁(eller₁ - v₁ ) (eller₁ + v₁ ) = m₂ (v₂ - eller₂) (v₂ + eller₂)

Nästa steg är att ersätta den första ekvationen i den andra:

m₂(v₂ - eller₂) (eller₁ + v₁ ) = m₂ (v₂ - eller₂) (v₂ + eller₂)

Och när termen upprepas m₂(v₂ - eller₂) På båda sidor av jämlikhet avbryts denna term och är så här:

(eller₁ + v₁) = (V₂ + eller₂)

Eller ännu bättre:

eller₁ - eller₂= v₂ -  v₁

Slutliga hastigheter v₁ och v₂ av partiklarna

Nu finns det två linjära ekvationer som det är lättare att arbeta. Vi placerar dem igen under den andra:

m₁eller₁ + m₂eller₂ = m₁v₁ + m₂v₂

eller₁ - eller₂= v₂ -  v₁

Multiplicera den andra ekvationen med m₁ Och lägga till termin till terminrester:

m₁eller₁ + m₂eller₂ = m₁v₁ + m₂v₂

m₁eller₁ - m₁eller₂= m₁v₂ - m₁ v₁

-

2 m₁eller₁ + (m₂ - m₁) eller₂ = (m₂ + m₁v₂

Och det är redan möjligt att rensa v₂. Till exempel:

En liknande behandling kan göras för att hitta en ekvation för v₁. Läsaren lämnas som en övning för att visa att:

Särskilda fall i elastiska kollisioner

Nu när ekvationerna är tillgängliga för de slutliga hastigheterna för båda partiklarna är det dags att analysera vissa speciella situationer.

Två identiska massor

Sedan m₁ = m₂ = m och:

v₁ = u₂

v₂ = u₁

Partiklar utbyter helt enkelt sina hastigheter efter kollision.

Två identiska massor, varav en ursprungligen var i vila

Igen  m₁ = m₂ = m och antar det eller₁ = 0:

v₁ = u₂

v₂ = 0

Efter kraschen förvärvar partikeln som var i vila samma hastighet på partikeln som hade rört sig, och det stannar i sin tur.

Kan tjäna dig: hydrauliskt tryck

Två olika massor, en av dem initialt i vila

Anta i det här fallet eller₁ = 0, Men massorna är olika:

Tänk om m₁ är mycket större än m₂?

Det händer att m₁ Hålla i vila och m₂ Det returneras med samma hastighet som den påverkade.

Huygens-Newton restitutionskoefficient eller regel

Tidigare härleddes följande samband mellan hastigheterna för två objekt i elastisk kollision: eller₁ - eller₂ = v₂ -  v₁. Dessa skillnader är de relativa hastigheterna före och efter kollisionen. I allmänhet uppfylls det för en kollision att:

eller₁ - eller₂ = -(v₁ -  v₂)

Det relativa hastighetskonceptet uppskattas bättre om läsaren föreställer sig att det är på en av partiklarna och från denna position observerar hastigheten med vilken den andra partikeln rör sig. Den föregående ekvationen skrivs om så här:

Om kinetisk energi inte bevaras kommer den angivna kvoten att vara mindre än 1. Låt oss ringa och till värdet av nämnda dimensionslösa kvotient:

Nåväl:

Värdet av och är mellan 0 och 1 och kallas restitutionskoefficient. När kollisionen är elastisk, e = 1. När det är helt inelastiskt, E = 0, medan om det har något annat mellanvärde har en del kinetiska energi spridit sig i andra typer av energi.

Löst övningar

-Motion Löst 1

En biljardkula rör sig till vänster vid 30 cm/s och kolliderar framifrån med en annan identisk boll som rör sig åt höger till 20 cm/s. De två bollarna har samma deg och kraschen är helt elastisk. Hitta hastigheten på varje boll efter påverkan.

Lösning

eller₁ = -30 cm/s

eller₂ = +20 cm/s

Detta är det speciella fallet att två identiska massor kolliderar i en elastiskt dimension, därför utbyts hastigheterna.

v₁ = +20 cm/s

v₂ = -30 cm/s

-Motion Löst 2

Restitutionskoefficienten för en boll som studsar på marken är lika med 0,82. Om du faller från vila, vilken bråkdel av din ursprungliga höjd kommer att nå bollen efter att ha hoppat en gång? Och efter 3 returer?

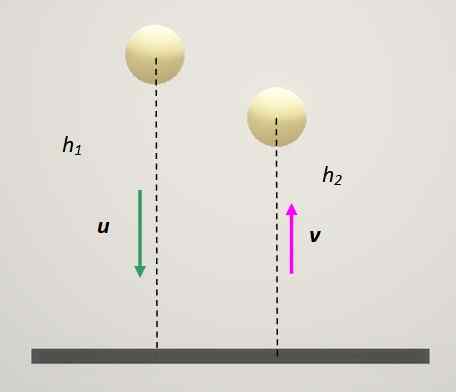En boll studsar mot en fast yta och tappar höjd med varje rebound. Källa: Självgjord.

Lösning

Jorden kan vara objekt 1 i restitutionskoefficientekvationen. Och det är alltid i vila, så att:

Den negativa riktningen väljs ner och den positiva. Hastigheten på ett objekt som fritt frigörs från en viss höjd h_antingen är:

Tecknet (-) indikerar att bollen går ner:

Det kan tjäna dig: Torricelli -experiment: Atmosfäriska tryckåtgärder, betydelse

 

Med denna hastighet studsar:

 

+ -Tecknet indikerar att det är en stigande hastighet. Och enligt den når bollen en maximal höjd på:

 

Nu återvänder han till marken igen med hastighet av samma storlek, men det motsatta tecknet:

Och studsar med:

Detta når en maximal höjd på:

Nå marken igen med:

På varandra följande returer

Varje gång bollen studsar och stiger upp måste du multiplicera hastigheten igen med 0.82:

Och når en maximal höjd bestämd av kvadratet med nämnda hastighet:

Vid denna tidpunkt h₃ är ungefär 30% av h_antingen. Vad skulle vara höjden vid 6: e returer utan att behöva göra beräkningar så detaljerade som de tidigare?

jag skulle vara h₆ = 0.82¹² h_antingen = 0.092h_antingen eller bara 9% av h_antingen.

-Motion löst 3

Ett 300 g block rör sig norrut till 50 cm/s och kolliderar mot ett 200 g block som riktas söderut 100 cm/s. Antag att kollisionen är helt elastisk. Hitta hastigheterna efter påverkan.

Data

m₁ = 300 g; eller₁ = + 50 cm/s

m₂ = 200 g; eller₂ = -100 cm/s

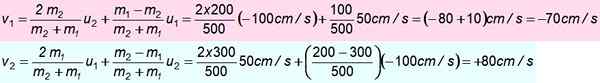
-Motion Löst 4

En massa M släpps₁ = 4 kg från den punkt som anges på banan utan friktion tills den kolliderar med M₂ = 10 kg i vila. Till vilken höjd är m₁ Efter kollisionen?

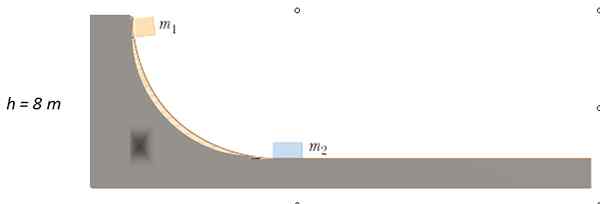
Lösning

Eftersom det inte finns någon friktion bevaras mekanisk energi för att hitta hastigheten eller₁ med vad m₁ effekter  m_2. Ursprungligen är kinetisk energi 0, sedan m₁ en del av resten. När den rör sig på den horisontella ytan har den ingen höjd, så den potentiella energin är 0.

Mgh = ½ mu₁ ²

 

eller₂ = 0

Nu hastigheten på m₁ Efter kollisionen:

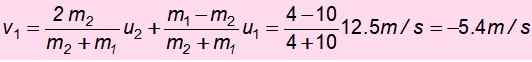
Det negativa tecknet innebär att det har återlämnats. Med denna hastighet stiger upp och mekanisk energi bevaras igen för att hitta H ', Höjden där den lyckas stiga upp efter kraschen:

½ mV₁² = mgh '

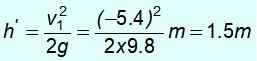
Observera att du inte återvänder till utgångspunkten på 8 m höjd. Den har inte tillräckligt med energi eftersom den gav en del av sin kinetiska energi massan m_1.

Referenser

1. Giancoli, D.  2006. Fysik: Principer med applikationer. 6^th. Ed Prentice Hall. 175-181
2. Rex, a. 2011. Fysikens grunder. Pearson. 135-155.
3. Serway, R., Vule, c. 2011. Fysikens grunder. 9^na Cengage Learning. 172 -182
4. Tipler, s. (2006) Fysik för vetenskap och teknik. 5: e upplagan. Volym 1. Redaktör. 217-238
5. Tippens, s. 2011. Fysik: koncept och applikationer. Sjunde upplagan. Macgraw Hill. 185 -195