Inelastiska sammanstötningar i en dimension och exempel

De Inelastiska chocker eller inelastiska kollisioner är en kort och intensiv interaktion mellan två föremål där rörelsemängden bevaras, men inte den kinetiska energin, varav en procentandel förvandlas till någon annan typ av energi.

Chocker eller kollisioner är ofta i naturen. Subatomära partiklar kolliderar i mycket höga hastigheter, medan många sporter och spel består av kontinuerliga kollisioner. Även galaxer kan kollidera.

Figur 1. Testbilskollision. Källa: Pixabay

Egentligen bevaras mängden rörelse i alla typer av kollisioner, så länge partiklarna kollideras av ett isolerat system. Så i den meningen finns det inga problem. Nu har föremål kinetisk energi förknippad med den rörelse de har. Vad kan hända med den energin när du kraschar?

De inre krafterna som äger rum under kollisionen mellan föremålen är intensiva. När det anges att kinetisk energi inte bevaras, betyder det att den förvandlas till andra typer av energi: till exempel i ljudenergi (en enhetskollision har ett distinkt ljud).

Fler användningsmöjligheter för kinetisk energi: Värme genom friktion, och naturligtvis den oundvikliga deformation som föremål lidit vid kollidering, till exempel bilkroppar i figuren ovan.

[TOC]

Exempel på inelastiska kollisioner 

- Två massor av plastin som kolliderar och möts tillsammans och rör sig som en bit efter kraschen.

- En gummiboll som studsar mot en vägg eller en golv. Bollen deformeras när du påverkar ytan.

Inte all kinetisk energi förvandlas till andra typer av energi, utom i få undantag. Objekt kan stanna hos en viss mängd av denna energi. Senare kommer vi att se hur man beräknar procentandelen.

När bitarna som kolliderar är länkade kallas kollisionen perfekt inelastisk och båda slutar vanligtvis att flytta tillsammans.

Perfekt inelastiska kollisioner i en dimension

Figurens kollision visar två föremål av olika massor m₁ och m₂, flytta till varandra med hastigheter v_i1 och v_I2 respektive. Allt händer på horisontellt, det vill säga det är en kollision i en dimension, det enklaste att studera.

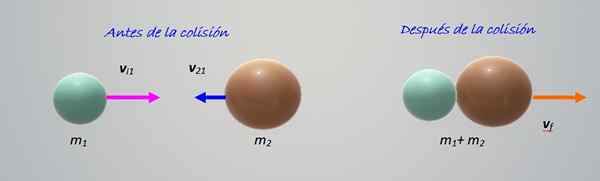figur 2. Kollision mellan två partiklar av olika massor. Källa: Självgjord.

Objekten kolliderar och sedan förenas till höger. Det är en perfekt inelastisk kollision, så det räcker att vi håller mängden rörelse:

P_antingen = P_F

Mängden rörelse är en vektor vars enheter är n.s. I den beskrivna situationen kan vektorotationen fördelas med eftersom det är kollisioner i en dimension:

Det kan tjäna dig: enkla fysikexperiment (primäruniversitet)

Mv_antingen = MV_F

Mängden rörelse för systemet är vektorsumman av mängden rörelse för varje partikel.

m₁ v_i1  + m₂ v_I2 = (m₁ + m₂v_F

Den slutliga hastigheten ges av:

v_F = (m₁ v_i1  + m₂ v_I2)/ (M₁ + m₂)

Restitutionskoefficient

Det finns ett belopp som kan indikera hur elastisk är en kollision. Det handlar om restitutionskoefficient, vilket definieras som det negativa förhållandet mellan partiklarnas relativa hastighet efter kraschen och den relativa hastigheten före kraschen.

Låt dig₁ och du₂ Partiklarnas respektive hastigheter initialt. Och vara v₁ och v₂ De respektive slutliga hastigheterna. Matematiskt kan restitutionskoefficienten uttryckas enligt följande:

Restitutionskoefficienten är en extra mängd, eftersom det är förhållandet mellan hastigheter. Men informationen är mycket intressant:

- Om ε = 0 motsvarar att säga att v₂ = v₁. Det betyder att de slutliga hastigheterna är desamma och kollisionen är inelastisk, som beskrivs i föregående avsnitt.

- När ε = 1 betyder att relativa hastigheter både före och efter kraschen inte förändras, i detta fall är kollisionen elastisk.

- Och om 0 < ε < 1 parte de la energía cinética de la colisión se transforma en alguna otra de las energías mencionadas anteriormente.

Hur man bestämmer restitutionskoefficienten?

Restitutionskoefficienten beror på klassen av material som är involverade i kollisionen. Ett mycket intressant test för att bestämma hur elastiskt är ett material för att göra bollar är att släppa bollen på en fast yta och mäta reboundhöjden.

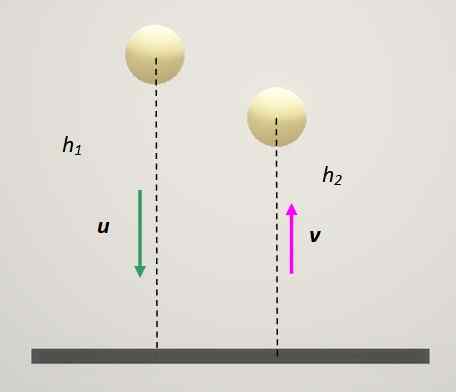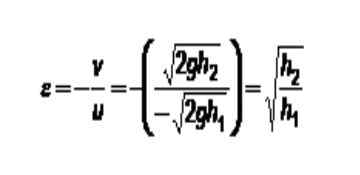
Figur 3. Metod för att bestämma restitutionskoefficienten. Källa: Självgjord.

I detta fall har den fasta plattan alltid hastighet 0. Om detta index 1 tilldelas detta och bollen är: Index 2 återstår:

Den initiala hastigheten beror på höjden h₁ från vilken han tappade:

Det negativa tecknet indikerar nedriktningen. Och den slutliga hastigheten är relaterad till den maximala höjden h₂ som når i rebound:

Ersätta i restitutionskoefficienten du har:

Explosioner

I början har det föreslagits att all kinetisk energi kan omvandlas genom att flytta till andra typer av energi. När allt kommer omkring förstörs energi inte. Är det möjligt att föremål som följde med rörelse kolliderar och sammanfogar och bildar ett enda objekt som plötsligt är i vila? Detta är inte så enkelt att föreställa sig.

Det kan tjäna dig: dynamik: historia, vilka studier, lagar och teorier

Låt oss dock föreställa oss vad som händer bakåt, som i en film som ses i baksidan. Sedan vilade objektet initialt och exploderar sedan fragmentering i flera delar. Denna situation är helt möjlig: det är en explosion.

Så att en explosion kan betraktas som en perfekt inelastisk kollision som ses bakåt i tid. Mängden rörelse bevaras också, att kunna bekräfta att:

P_antingen = P_F

Löst exempel

-Övning 1

Det är känt från mätningar att stålåterställningskoefficienten är 0.90. En stålkula tappas från 7 m hög på en fast platta. Beräkna:

a) tills vilken höjd kommer att studsa.

b) Hur lång tid tar det mellan den första kontakten med ytan och den andra.

Lösning

a) Ekvationen som tidigare härleddes i avsnittet om bestämning av restitutionskoefficienten används:

Höjd rensar h₂:

0.90² . 7 m = 5.67 m

b) att höja 5.67 meter en hastighet som ges av:

Varifrån:

Och tiden det tar att nå denna höjd är:

t _Max = v_antingen/ g = (10.54/9.8 s) = 1.08 s.

Den tid det tar att återvända är densamma, därför den totala tiden att ladda upp 5.67 meter och återgår till utgångspunkten är dubbelt så mycket som den maximala tiden:

t_flyg = 2.15 s.

-Övning 2

Figuren visar ett block av trä av massa m hängande vid resten av trådarna med längd som pendel. Detta kallas den ballistiska pendeln och tjänar till att mäta hastighet V för inträde en massa av massa m. Ju högre hastighet med vilken kulan påverkar blocket, i en högre höjd H kommer detta att byggas.

Bildkulan är inbäddad i blocket, därför är den en helt inelastisk chock.

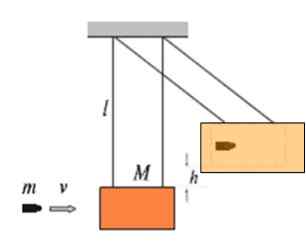Figur 4. Den ballistiska pendeln.

Antag att en 9 9.72 g påverkan mot massblocket 4.60 kg, sedan stiger uppsättningen till 16.8 cm av jämviktspositionen. Vad är hastigheten v av kulan?

Lösning

Under kollisionen bevaras mängden rörelse och eller_F Det är hastigheten på uppsättningen, när kulan har inbäddat i blocket:

P_antingen = P_F

Blocket vilar initialt, medan kulan riktas till målet med hastighet v:

m.v + m.0 = (m + m) u_F

 

Det är inte känt eller_F Även, men efter kollision bevaras mekanisk energi, detta är summan av gravitationspotentialenergi och kinetisk energi K:

Kan tjäna dig: summan av vektorer: grafisk metod, exempel, lösta övningar

Initial mekanisk energi = slutlig mekanisk energi

OCH_mo = E_Mf

ELLER_antingen + K_antingen = U_F + K_F

Gravitationspotential energi beror på höjden vid vilken uppsättningen når. För jämviktspositionen är den initiala höjden den som tas som referensnivå därför:

ELLER_antingen = 0

Tack vare kulan har uppsättningen kinetisk energi K_antingen, som blir gravitationspotential energi när uppsättningen når sin maximala höjd h. Kinetisk energi ges av:

K = ½ mV²

Ursprungligen är kinetisk energi:

K_antingen = (1/2) (m+m) u_F²

Kom ihåg att kulan och blocket bildar ett enda massobjekt M+ m. Gravitationspotentialenergin när de har nått i sin maximala höjd är:

ELLER_F = (m + m) gh

Därför:

K_antingen = U_F

(1/2) (m+m) u_F² = (m + m) gh

Nu ersätts detta resultat i uttryck till v som rensades i början, från bevarande av mängden rörelse:

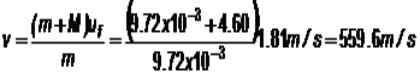
-Övning 3

Syftet med figuren exploderar i tre fragment: två av lika massa m och en större av massan 2m. Figuren indikerar hastigheterna för varje fragment efter explosionen. Vad var det ursprungliga målet med objektet?

Figur 5. Stenen som exploderar i 3 fragment. Källa: Självgjord.

Lösning

Detta problem kräver användning av två koordinater: x och och, Eftersom två av fragmenten har vertikala hastigheter, medan de återstående har horisontell hastighet.

Objektets totala massa är summan av massan för alla fragment:

M = m + m + 2m = 4m

Mängden rörelse bevaras både på x -axeln och på y -axeln föreslås det separat:

1. 4m. eller_x= m v₃
2. 4m. eller_och = m. 2v₁ - 2m. v₁

Observera att det stora fragmentet rör sig ner med V1 -hastighet, för att påpeka detta faktum har ett negativt tecken placerats.

Från den andra ekvationen följer det omedelbart det eller_och = 0, Och den första är tydlig UX omedelbart:

Objektets initiala mål var u_antingen = u_x = v₃/4.

Referenser

1. Giancoli, D.  2006. Fysik: Principer med applikationer. 6^th. Ed Prentice Hall. 175-181
2. Rex, a. 2011. Fysikens grunder. Pearson. 135-155.
3. Serway, R., Vule, c. 2011. Fysikens grunder. 9^na Cengage Learning. 172 -182
4. Tipler, s. (2006) Fysik för vetenskap och teknik. 5: e upplagan. Volym 1. Redaktör. 217-238
5. Tippens, s. 2011. Fysik: koncept och applikationer. Sjunde upplagan. Macgraw Hill. 185 -195