Kallas Betydande siffror till mängden siffror som innehåller Mantisa av ett nummer. Ju fler siffror mängden är känd med den största precisionen. Som en påminnelse är Mantisa den figur som följer med kraften på 10 när antalet i vetenskaplig notation skrivs.

Låt oss till exempel ta nummer 0.00376, som är skriven som 3.76 x 10 ^-3. Mantisa är 3.76 och antalet har totalt 3 betydande siffror. Numret 0.129 har också 3 betydande siffror, medan 4.5 har bara 2.

Figur 1. Vetenskapliga kalkylatorer visar aldrig antalet betydande siffror för en operation. Källa: Piqsels.

Och vad händer när numret är hel? Det betyder att det är känt med all möjlig precision, med andra ord har det oändligt precision. Till exempel, genom att räkna människor, djur eller föremål som böcker och telefoner, är resultatet ett heltal och exakt antal.

Om vi ​​säger att det i en biograf finns 110 personer som tittar på en film är detta det exakta antalet, varken mer eller mindre och har 3 betydande figurer.

Betydande siffror hanteras av några enkla regler som memoreras med lite övning, som vi kommer att se då.

[TOC]

Regler för att bestämma de betydande siffrorna för ett nummer

Regel 1

De föregående nollorna räknas inte som en betydande figur, så 0.045 och 4.5 De har båda två betydande siffror, eftersom dessa börjar räknas från vänster och börjar från den första olika siffran med noll.

Regel 2

De bakre nollorna (till höger) till den första betydande siffran räknas som en betydande figur (så länge den är motiverad av mätinstrumentets noggrannhet).

Slutligen räknas nollorna som finns i mitten också som betydande siffra.

Regel 3

För siffrorna som skrivs i vetenskaplig notation är alla mantisa -siffror betydande, och exponenten påverkar inte precision.

Det kan tjäna dig: medelhastighet: formler, hur det beräknas och löses

Regel 4

När operationer med decimaler görs, till exempel genom att beräkna områden eller andra liknande operationer, måste resultatet ha samma antal betydande siffror som beloppet med det lägsta antalet betydande siffror som deltog i operationen. Denna regel är giltig för alla aritmetiska operationer.

Regel 5

Antalet antalet påverkar inte antalet betydande siffror.

Vi kommer omedelbart att se några exempel på detta och alla andra regler.

Exempel

Exempel 1

Hitta hur många betydande siffror som finns i vart och ett av dessa siffror.

a) 876

b) 1000.68

c) 0.00005026

d) 4.8

e) -6.99

Svar

a) 876 har 3 betydande siffror.

b) 1000.68 har 6 betydande siffror, eftersom nollor i mitten räknas som sådan.

c) istället 0.00005026 har fyra betydande siffror. Observera att de 5 nollorna till vänster om de 5 inte räknas som en betydande figur, istället på 0 mellan 5 och 2 Ja.

d) 4.8 har 2 betydande siffror.

e) -6.99 har 3 betydande siffror.

Exempel 2

Det är vanligt att vidta åtgärder, såsom metriska band, klockor, termometrar, skalor och så på stilen. Hur många betydande siffror ska vi rapportera de belopp som vi mäter på detta sätt?

Svar

Det beror på uppskattningen av instrumentet som det mäts. Låt oss sätta ett exempel: Mät det yttre diametern på ett rör, med en graderad regel och med Vernier eller King's Foot.

Vernier är ett instrument som mäter längderna mycket just för att det har en extra liten skala, kallad nonieskala, vilket möjliggör större finhet, så att säga, vid mätning.

Det är mer exakt än en graderad regel eftersom vi med det kan lära oss mer betydande figurer av en viss längd.

Det är därför det inte är meningsfullt att rapportera en omkrets av, säg, 35.88 cm om vi mäter det med måttband, eftersom detta instrument inte är tillräckligt exakt för att rapportera så många betydande siffror.

Kan tjäna dig: statisk: historia, vilka studier, applikationer, lagar

Uppskattningen av bandmåttet ges av:

För ett måttband eller en millimeterregel, a = 1 mm, som är tionde av en centimeter. Omkretsen uppmätt med mättejp måste rapporteras som 35.9 cm.

Exempel 3

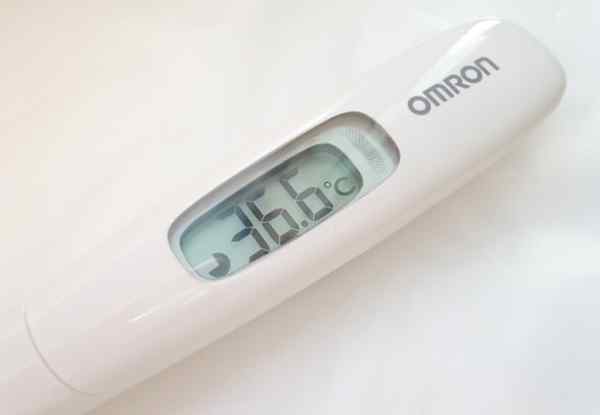
Hur många betydande siffror har läsning gjord med den digitala termometern?

Svar

Figurens termometer erbjuder temperaturavläsningar med tre siffror. Men i den utsträckning som visas, 36.6 ºC, endast de två första siffrorna från vänster till höger är exakta, eftersom decimalen påverkas av instrumentets uppskattningsfel, som vanligtvis anges på baksidan av samma eller i dess verksamhetsmanual.

Den vanliga saken för den typ av digitalt instrument som visas är ett fel i 0 uppskattning.1 ºC. Detta räcker för att vara säker på att det inte finns någon feber.

figur 2. Digital termometer vars avläsningar är 3 betydande siffror. Källa: Pxhere.

Regler för runda nummer

När en kalkylator används för att utföra beräkningar med erhållna åtgärder är det inte korrekt att ge resultatet med alla siffror som visas på skärmen.

Endast de som känner varandra exakt behålls, för bara de har verklig mening. Då är det nödvändigt att avrunda resultaten för att passa antalet siffror som är kända exakt. Dessa regler är:

-Om antalet som följer den siffran som ska behållas är lika med eller större än 5, Till denna siffra läggs till 1.

Till exempel genom att runda 3.786 För att ha två decimaler vill vi behålla siffrorna till 8. Eftersom antalet som följer (6) är större än 5 blir 8 + 1 = 9 och antalet kvarstår 3.79.

-När antalet som följer den siffran som ska behållas är Mindre än 5, Siffran är densamma.

Kan tjäna dig: Joule Effect: Förklaring, exempel, övningar, applikationer

Om vi ​​vill runda 1.27924 För att endast ha tre decimaler uppnås detta genom att nå 9, vilket följs av en 2. Eftersom de 2 är mindre än 5 försvinner dessa decimaler och det rundade antalet är 1.279.

Träning löst

Ett matbord har formen och dimensionerna som anges i den bifogade figuren. Det uppmanas att beräkna sitt område med hjälp av reglerna för verksamheten med betydande siffror.

Lösning

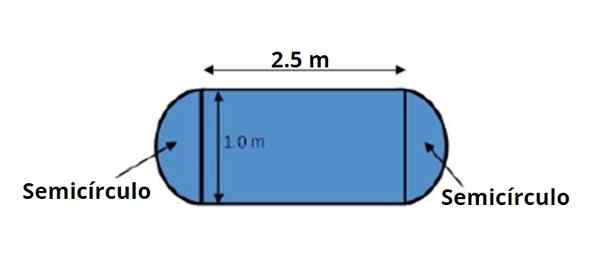Figur 3. En tabell har den form och dimensioner som anges i figuren, märk att dessa är kända med två betydande figurer. Källa: f. Zapata.

Tabellområdet kan delas upp i ett centralt rektangulärt område och två halvcirklar, ett på varje sida, som tillsammans gör 1 hela cirkeln.

Vi ringer₁ till rektangelområdet, ges av:

TILL₁ = bas × höjd = 2.5 m x 1.0 m = 2.5 m²

För sin del är cirkelområdet, som motsvarar det för 1 halvcirkel multiplicerad med 2:

TILL₂ = π × radio²

Diametern på någon av halvcirklarna är 1.0 m, därför är radien 0.50 m. Diametern kan också användas direkt för att beräkna området, i detta fall:

TILL₂ = (π × diameter²) / 4

Hur som helst:

TILL₂ = [π x (1.0 m)²] / 4 = 0.785398163 m²

Alla siffror som erbjuds av räknaren användes. Nu lägger vi till till₁ redan₂ För tabellens totala yta:

A = (2.5 + 0.785398163) m² = 3.285398163 M²

Eftersom tabellens dimensioner är kända med två betydande siffror är det inte meningsfullt att uttrycka resultatet med alla decimaler som ges av räknaren, som aldrig ger antalet betydande siffror för ett resultat.

Det som måste göras är att runda området så att det har samma antal betydande siffror som bordets dimensioner, det vill säga 2. Därför rapporteras det slutliga resultatet så här:

A = 3.3 m²

Referenser

1. Bauer, w. 2011. Fysik för teknik och vetenskap. Volym 1. MC Graw Hill.
2. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volym 1. Kinematik. Redigerad av Douglas Figueroa (USB).
3. Fisisk. Betydande siffror och avrundning. Återhämtat sig från: Fisicalab.com.
4. Giancoli, D.  2006. Fysik: Principer med applikationer. Sjätte. Ed Prentice Hall.
5. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14th. Ed. Volym 1.