Rektangulära komponenter i en vektor (med övningar)

De rektangulära komponenter i en vektor är data som utgör denna vektor. För att bestämma dem är det nödvändigt att ha ett koordinatsystem, som vanligtvis är det kartesiska planet.

När du har en vektor i ett koordinatsystem kan dess komponenter beräknas. Dessa är 2, en horisontell komponent (parallell med x -axeln), kallad "komponent i x -axeln" och en vertikal komponent (parallell med y -axeln), kallad "komponent i y -axeln" ".

Grafisk representation av de rektangulära komponenterna i en vektor

För att bestämma komponenterna är det nödvändigt.

[TOC]

Hur man bestämmer de rektangulära komponenterna i en vektor?

För att bestämma dessa komponenter måste vissa förhållanden mellan rektanglar och trigonometriska funktioner vara kända.

I följande bild kan du se det här förhållandet.

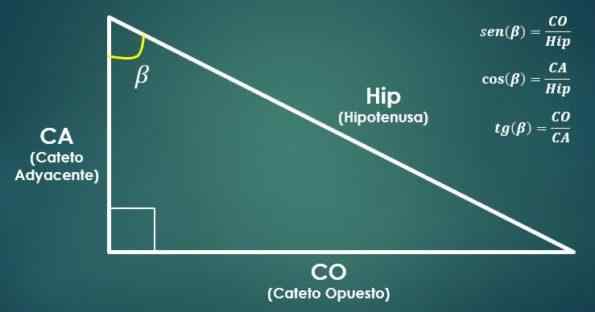Förhållanden mellan rektanglar och trigonometriska funktioner

Vinkeln är lika med kvoten mellan måttet på kateto som motsätter sig vinkeln och måtten på hypotenusen.

Å andra sidan är kosinusen i en vinkel lika med kvoten mellan måttet på kateto intill vinkeln och måtten på hypotenusen.

Tangenten av en vinkel är lika med kvoten mellan måttet på det motsatta benet och måtten på den intilliggande kateto.

I alla dessa relationer är det nödvändigt att etablera motsvarande rektangel triangel.

Finns det andra metoder?

Ja. Beroende på de uppgifter som tillhandahålls kan sättet att beräkna de rektangulära komponenterna i en vektor variera. Ett annat verktyg som används mycket är Pythagoras teorem.

Kan tjäna dig: existens och unikhetsteorem: demonstration, exempel och övningar

Löst övningar

Följande övningar genomförde definitionen av de rektangulära komponenterna i en vektor och förhållandena som beskrivs ovan.

Första träning

Det är känt att en vektor A har storlek lika med 12 och vinkeln som denna form med x -axeln har ett 30 ° mått. Bestämma de rektangulära komponenterna i nämnda vektor till.

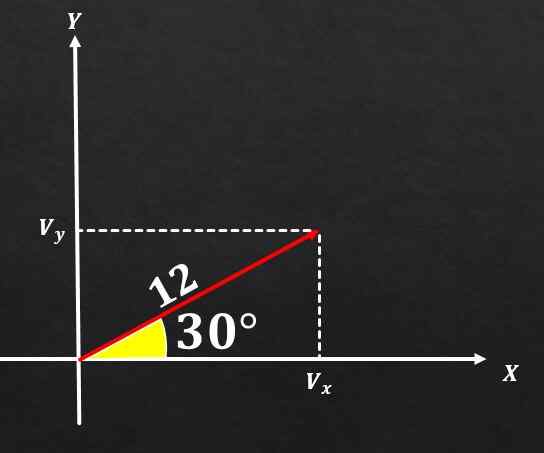
Lösning

Om bilden uppskattas och formlerna som beskrivs ovan används kan man dra slutsatsen att komponenten i och vektor A är lika med

synd (30 °) = vy / 12, och därför vy = 12*(1/2) = 6.

Å andra sidan är komponenten på x -axeln för vektor A lika med

cos (30 °) = vx / 12, och därför Vx = 12*(√3 / 2) = 6√3.

Andra träning

Om vektor A har en storlek lika med 5 och komponenten på x -axeln är lika med 4, bestäm värdet på A -komponenten på Y -axeln.

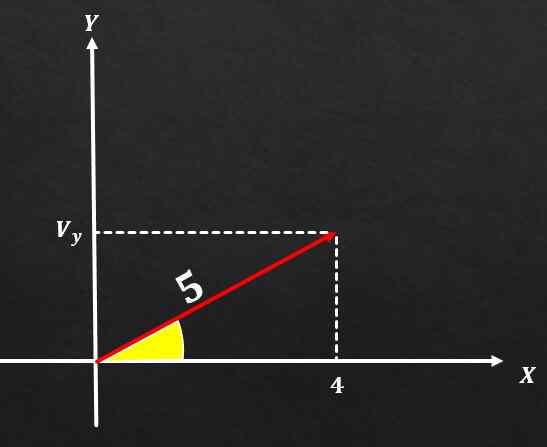
Lösning

Med hjälp av Pythagoras teorem måste vektorns storlek en hög kvadrat vara lika med summan av rutorna i de två rektangulära komponenterna. Det vill säga m² = (vx) ² + (vy) ².

Ersätta de angivna värdena måste du

5² = (4) ² + (vy) ², därför 25 = 16 + (vy) ².

Detta innebär att (vy) ² = 9 och följaktligen vy = 3.

Tredje träning

Om vektor A har en storlek lika med 4 och denna bildar en vinkel på 45 ° med X -axeln, bestäm de rektangulära komponenterna i nämnda vektor.

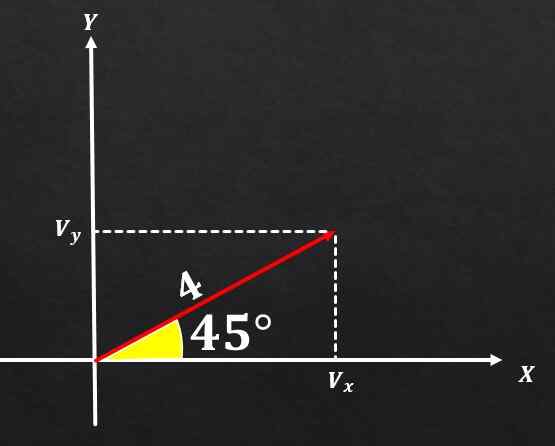
Lösning

Med hjälp av förhållandena mellan en rektangel triangel och trigonometriska funktioner kan man dra slutsatsen att komponenten på och vektor a är lika med

synd (45 °) = vy / 4, och därför vy = 4*(√2 / 2) = 2√2.

Å andra sidan är komponenten på x -axeln för vektor A lika med

Kan tjäna dig: sammansatt succession

cos (45 °) = Vx / 4, och därför Vx = 4*(√2 / 2) = 2√2.

Referenser

1. Landaverde, f. D. (1997). Geometri (Omtryck ed.). Framsteg.
2. Leake, D. (2006). Trianglar (Illustrerad ED.). Heinemann-raintree.
3. Pérez, c. D. (2006). Förkalkning. Pearson Education.
4. Ruiz, á., & Barrantes, h. (2006). Geometrier. Cr teknologisk.
5. Sullivan, m. (1997). Förkalkning. Pearson Education.
6. Sullivan, m. (1997). Trigonometri och analytisk geometri. Pearson Education.