Matematik

Externa alternativa vinklar övningar och övningar löst

Externa alternativa vinklar övningar och övningar löst

De yttre alternativa vinklar De är de vinklar som bildas när två parallella linjer avlyssnas med en torklinje. Förutom dessa vinklar bildas ett annat vridmoment som kallas inre alternativa vinklar.

Skillnaden mellan dessa två koncept är de "externa" och "interna" orden och som det angivna namnet är de yttre alternativa vinklarna de som bildas utanför de två parallella linjerna.

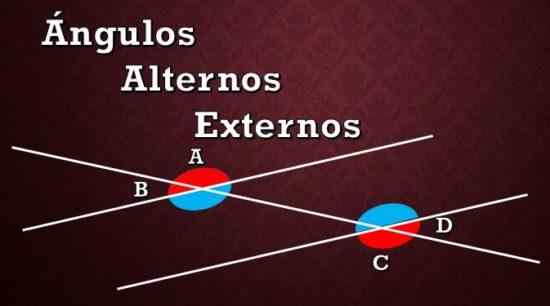
Grafisk representation av alternativa yttre vinklar A, B och C, D

Som framgår av den föregående bilden finns det åtta vinklar som bildas mellan de två parallella linjerna och torklinjen. De röda vinklarna är de yttre alternativen, och de blå vinklarna är de inre alternativa vinklarna.

[TOC]

Egenskaper hos yttre alternativa vinklar

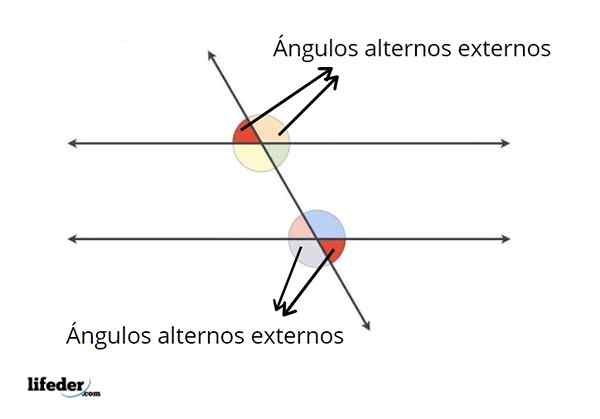Exempel på yttre alternativa vinklar

I inledningen förklarades redan vad de yttre alternativa vinklarna är. Förutom att de är de yttre vinklarna mellan parallellerna uppfyller dessa vinklar ett annat tillstånd.

Villkoret de uppfyller är att de yttre alternativa vinklar som bildas på en parallell linje är kongruenta; Den har samma mått som de andra två som bildas på den andra parallella linjen.

Men varje yttre alternativ vinkel överensstämmer med den på andra sidan Secant -linjen.

Vilka är de kongruenta yttre alternativa vinklar?

Om bilden av början och den tidigare förklaringen observeras kan man dra slutsatsen att de yttre alternativa vinklar som är överensstämmande med varandra är: vinklar A och C och vinklar B och D.

Att visa att de är kongruenta.

Kan tjäna dig: konstant funktion: egenskaper, exempel, övningar

Löst övningar

Nedan följer en serie övningar där definitionen och egenskapen för kongruens av de yttre alternativa vinklar måste tillämpas.

Första träning

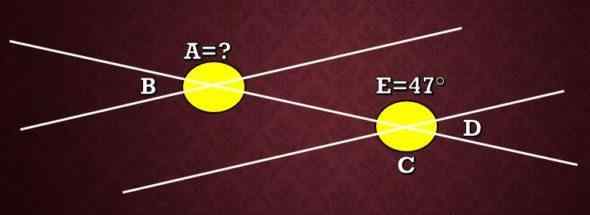
I följande bild, vad är måttet på vinkel A och vet att vinkeln E mäter 47 °?

Lösning

Som förklarats tidigare är vinklar A och C kongruenta för att vara externa alternativa. Därför är måttet på A lika med måttet på C. Nu, eftersom vinklarna E och C är motsatta vinklar med toppunkten, har de att de har samma mått, därför är måttet på C 47 °.

Sammanfattningsvis är åtgärden lika med 47 °.

Andra träning

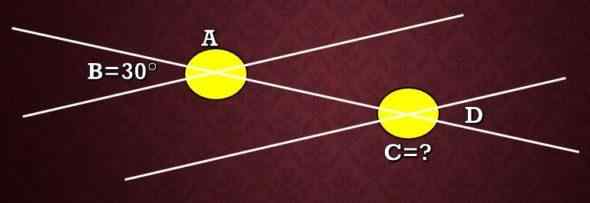
Beräkna måttet på vinkel C som visas i följande bild, och vet att vinkel B mäter 30 °.

Lösning

I det här exemplet används definitionen. Två vinklar är kompletterande om summan av deras åtgärder är lika med 180 °.

På bilden kan man se att A och B är kompletterande, därför A+B = 180 °, det vill säga vid+30 ° = 180 ° och därför A = 150 °. Nu, som A och C är de yttre alternativa vinklar, så dess åtgärder är desamma. Därför är C -måttet 150 °.

Tredje träning

I följande bild är måtten på vinkel A 145 °. Vad är måttet på vinkel E?

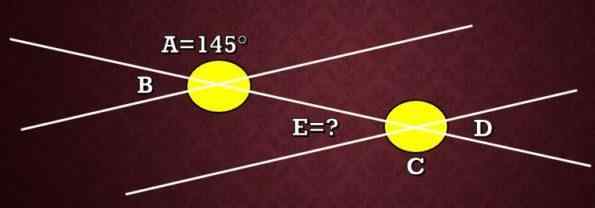
Lösning

På bilden kan man se att vinklar A och C är yttre alternativa vinklar, därför har de samma mått. Det vill säga att måttet på C är 145 °.

Eftersom vinklar C och E är kompletterande vinklar måste den vara C+E = 180 °, det vill säga 145 °+E = 180 ° och därför är måttet på vinkel E 35 °.

Kan tjäna dig: provtagningsfel: formler och ekvationer, beräkning, exempel

Referenser

  1. Burke. (2007). En vinkel på geometri matematik arbetsbok. Newpath Learning.
  2. C. OCH. TILL. (2003). Geometrielement: med många övningar och kompassgeometri. University of Medellin.
  3. Clemens, s. R., O'DAFER, s. G., & Cooney, T. J. (1998). Geometri. Pearson Education.
  4. Lang, s., & Murrow, g. (1988). Geometri: En gymnasiet. Springer Science & Business Media.
  5. Lira, a., Jaime, s., Chavez, m., Gallegos, m., & Rodríguez, c. (2006). Geometri och trigonometri. Paraplyutgåvor.
  6. Moyano, a. R., Saro, A. R., & Ruiz, r. M. (2007). Algebra och kvadratisk geometri. Netbiblo.
  7. Palmer, C. Yo., & Bibb, s. F. (1979). Praktisk matematik: Aritmetik, algebra, geometri, trigonometri och beräkningsregel. Reverte.
  8. Sullivan, m. (1997). Trigonometri och analytisk geometri. Pearson Education.
  9. Wingard-enelson, r. (2012). Geometri. Enslow Publishers, Inc.