Äktenskapliga fastigheter, exempel, övningar löst

Det förstås av Ändlig uppsättning alla inställda med ett begränsat eller redovisningsantal av element. Exempel på ändliga uppsättningar är kulor som finns i en väska, uppsättningen av hem i ett område eller uppsättningen P bildas av de tjugo (20) naturliga siffrorna:

P = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,13, 14, 16, 17, 18, 19, 20 

Uppsättningen av Universe Stars är säkert enorm, men det är inte känt säkert om det är begränsat eller oändligt. Uppsättningen av solsystemplaneter är dock begränsad.

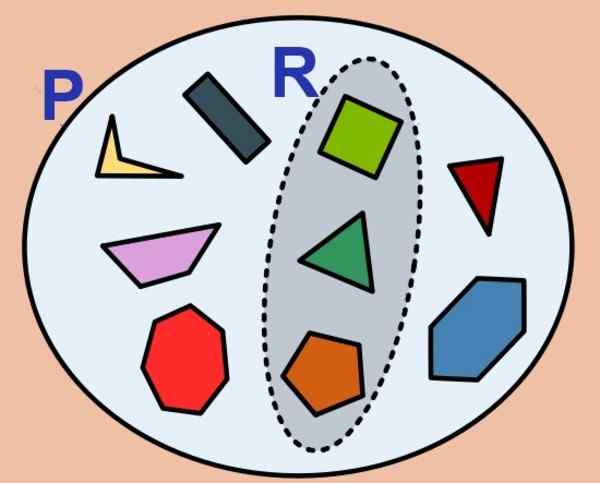
Figur 1. Uppsättningen polygoner är begränsad och delmängden av de vanliga. (Wikimedia Commons)

Antalet element i en ändlig uppsättning kallas dess kardinalitet och för uppsättningen P Det betecknas så här: kort (P) antingen #P. Den tomma uppsättningen har nollkardinalitet och anses vara en ändlig uppsättning.

[TOC]

Egenskaper

Bland egenskaperna för ändliga uppsättningar är följande:

1- Union of Finite Set resulterar i en ny ändlig uppsättning.

2- Om två ändliga uppsättningar avlyssnas är det en ny ändlig uppsättning.

3- En delmängd av en ändlig uppsättning är ändlig och dess kardinalitet är mindre än eller lika med den för den ursprungliga uppsättningen.

4- Den tomma uppsättningen är en ändlig uppsättning.

Exempel

Det finns många exempel på ändliga uppsättningar. Bland några exempel är följande:

Uppsättning M av årets månader, som kan förlängas enligt följande:

M = Januari, februari, mars, april, maj, juni, juli, augusti, september, oktober, november, december, kardinaliteten för M är 12.

Uppsättning S av veckodagarna: S = Måndag, tisdag, onsdag, torsdag, fredag, lördag, söndag. Kardinaliteten är 7.

Kan tjäna dig: proportionalitetsrelationer: koncept, exempel och övningar

Uppsättning Ñ Från bokstäverna i det spanska alfabetet är det en ändlig uppsättning, denna uppsättning i förlängningen skrivs så här:

Ñ = A, B, C, D, E, F, G, H, I, J, K, L, M, N, ñ, O, P, Q, R, S, T, U, V, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, X, Y, Z och dess Kardinalitet är 27.

Uppsättning V Från vokalerna på spanska är det en delmängd av ñ -uppsättningen:

V ⊂ Ñ Därför är det en ändlig uppsättning.

Den ändliga uppsättningen V Utökat sätt det är skrivet så här: V = A, E, I, O, U och dess kardinalitet är 5.

Uppsättningar kan uttryckas genom att förstå. Uppsättning F som består av bokstäverna i ordet "ändligt" är ett exempel:

F = x / x är en bokstav i ordet "ändlig"

Denna uppsättning uttryckt i stor utsträckning kommer att vara:

F = f, i, n, t, o vars kardinalitet är 5 och därför är det en ändlig uppsättning.

Fler exempel

Regnbågens färger är ett annat ändligt set -exempel, uppsättningen C av dessa färger är:

C = röd, orange, gul, grön, cyan, blå, violet och dess kardinalitet är 7.

Uppsättningen av faser F Från månen är ett annat ändligt exempel:

F = New Moon, Growing Room, Full Moon, Waning Room Denna uppsättning har kardinalitet 4.

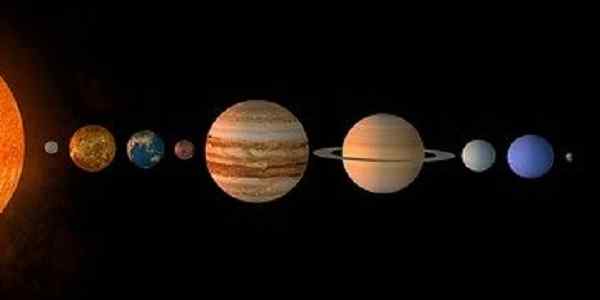figur 2. Solsystemets planeter bildar en ändlig uppsättning. (Pixabay)

En annan ändlig uppsättning är den som bildas av planeterna i solsystemet:

P = Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, Neptune, Pluto Kardinalitet 9.

Löst övningar

Övning 1

Följande uppsättning ges a = x∊ r / x^3 = 27. Uttrycka det i ord och skriv det i förlängningen, ange dess kardinalitet och säga om det är ändligt eller inte.

Kan tjäna dig: ellipse

Lösning: Set A är uppsättningen av verkliga siffror X så att X höjs till kuben som ett resultat 27.

Ekvation x^3 = 27 har tre lösningar: som är x1 = 3, x2 = (-3/2 + 3√3/2 i) och x3 = (-3/2-3√3/2 i). Av de tre lösningarna är endast x1 verkliga, medan de andra två är komplexa siffror.

Eftersom definitionen av uppsättning A säger att X tillhör riktiga siffror, så är lösningar i komplexa siffror inte en del av uppsättningen till.

Den utökade uppsättningen är:

A = 3, som är en ändlig uppsättning av kardinalitet 1.

Övning 2

Skriv symboliskt (genom att förstå) och omfattande uppsättningen B för de verkliga siffrorna som är större än 0 (noll) och mindre eller lika än 0 (noll). Ange din kardinalitet och om den är ändlig eller inte.

Lösning: B = x∊ r / 0 < x <= 0

Set B är tomt eftersom ett riktigt nummer X inte kan vara samtidigt större och mindre än noll, såväl som 0 och också mindre än 0.

B = och dess kardinalitet är 0. Den tomma uppsättningen är en ändlig uppsättning.

Övning 3

S -uppsättningen av lösningarna för en viss ekvation ges. Uppsättningen av förståelse är skriven så här:

S = x∊ r / (x -3) (x^2 - 9x + 20) = 0

Skriv denna uppsättning i stor utsträckning, ange din kardinalitet och ange om det är en ändlig uppsättning eller inte.

Lösning: Först, genom att analysera uttrycket som beskriver uppsättningarna, erhålls det att det är en uppsättning verkliga X -värden som är lösningar för ekvationen:

(x -3) (x^2 - 9x + 20) = 0 (*)

En lösning av denna ekvation är x = 3, vilket är ett verkligt antal och tillhör därför s. Men det finns fler lösningar som kan erhållas och leta efter lösningarna i den kvadratiska ekvationen:

Kan tjäna dig: Distribution F: Egenskaper och övningar löst

(x^2 - 9x + 20) = 0

Det tidigare uttrycket kan faktor enligt följande:

(x - 4) (x - 5) = 0

Vilket leder oss till ytterligare två lösningar av den ursprungliga (*) ekvationen som är x = 4 och x = 5. Kort sagt, ekvation (*) har lösningar 3, 4 och 5.

S -uppsättningen uttryckt i stor utsträckning är så här:

S = 3, 4, 5, som har kardinalitet 3 och därför är en ändlig uppsättning.

Övning 4

Det finns två uppsättningar a = 1, 5, 7, 9, 11 och b = x ∊ n / x är par ^ x x < 10 .

Skriv uttryckligen set B och hitta facket med uppsättningen a. Hitta också avlyssningen av dessa två uppsättningar och avslut.

Lösning: Set B består av naturliga siffror så att de är jämna och också är lägre än värde 10, därför skrivs B tillsammans B är tillsammans enligt följande:

B = 2, 4, 6, 8

Föreningen av uppsättning A med uppsättning B är:

A U B = 1, 2, 4, 5, 6, 7, 8, 9, 11

och avlyssningen av uppsättning A med uppsättning B är skriven så här:

A ⋂ B = = Ø är den tomma uppsättningen. 

Det bör noteras att unionen och avlyssningen av dessa två ändliga uppsättningar leder till nya uppsättningar, som i sin tur också är begränsade.

Referenser

1. Källor, a. (2016). Grundläggande matematik. En introduktion till beräkning. Lulu.com.
2. Garo, m. (2014). Matematik: Kvadratiska ekvationer: Hur löser en kvadratisk ekvation. Marilù garo.
3. Haeussler, E. F., & Paul, r. S. (2003). Matematik för administration och ekonomi. Pearson Education.
4. Jiménez, J., Rodríguez, m., Estrada, r. (2005). Matematik 1 september. Tröskel.
5. Dyrbar, c. T. (2005). Matematikkurs 3o. Redaktionell progreso.
6. Matematik 10 (2018). "Exempel på ändliga uppsättningar". Hämtad från: Matematik10.netto
7. Rock, n. M. (2006). Algebra I är lätt! Så enkelt. Team Rock Press.
8. Sullivan, J. (2006). Algebra och trigonometri. Pearson Education.
9. Wikipedia. Ändlig uppsättning. Återhämtad från: är.Wikipedia.com